Two Realization Schemes Raise Hopes for Superconducting Quantum Bits

Quantum computers have the potential to perform tasks exponentially faster than classical computers. Key to this speedup is the massive parallelism and entanglement arising from the superposition of states in quantum bits, or qubits. But the requisite quantum coherence is very fragile, and can be lost through interactions with the environment or other noise sources (see the article by John Preskill in Physics Today, June 1999, page 24 ).

Therein lies the challenge of building a real quantum computer: Qubits must be sufficiently isolated from the environment so that they can maintain their coherence throughout the computation. But they must also be sufficiently coupled to the outside world to allow controlled state preparation, manipulation, and measurement.

Much of the experimental attention has been focused on qubit implementations involving nuclear magnetic resonance or trapped ions. Superconducting circuits, long a dark horse in the qubit race, have recently attracted much attention with two reports, one by the Quantronics group at the Atomic Energy Commission (CEA) in Saclay, France, ¹ and one by Siyuan Han and coworkers at the University of Kansas. ² Both groups achieved coherent control with long coherence times, an important step in the quest for quantum information processors.

Charge and flux regimes

The solid state nature of superconducting circuits has both advantages and disadvantages for implementing qubits. Some researchers welcome the familiarity of all-electrical devices controlled by currents and voltages. And well-established lithography techniques should facilitate scaling up the circuits to include larger numbers of qubits. But unlike NMR and trapped-ion qubit implementations, in which the controlling radio-frequency or laser pulses can be turned on and off as needed, the electrical leads that connect a superconducting qubit to the outside world are always present. As a result, environmentally induced decoherence is an even larger obstacle to overcome in superconducting systems.

In a superconductor, the number of Cooper pairs and the phase of the wavefunction are conjugate variables. Most of the research into superconducting qubits has focused either on the charge regime, in which the number of Cooper pairs is well defined, or on the flux regime, in which the phase is well defined. ³

In the charge regime, a small superconducting island—a so-called Cooper-pair box—is connected to the outside world by one or two Josephson junctions. If the junction capacitances are sufficiently small, the number of Cooper pairs on the island is well defined at millikelvin temperatures. A voltage applied to a gate electrode capacitively coupled to the island can draw additional Cooper pairs onto the island through one of the Josephson junctions. Two charge states of the island, differing by one Cooper pair, can form the basis states for the qubit.

Three years ago, Yasunobu Nakamura and colleagues at NEC Corp in Tsukuba, Japan, succeeded in preparing a Cooper-pair box in a superposition of two charge states. ⁴ They brought the states into resonance by applying a suitably tuned voltage pulse to the gate electrode. Coherent oscillations between the states were reflected in occupation probabilities that varied sinusoidally with the pulse duration. The oscillations were short-lived, however, damping out after only a few nanoseconds. Fluctuations in the background charge distribution in the circuit’s oxide layers and substrate were suspected as the largest source of decoherence.

In the flux regime, the qubit devices resemble superconducting quantum interference devices (SQUIDs). When an applied magnetic field threads a superconducting loop containing Josephson junctions, a supercurrent is induced that increases or decreases the enclosed flux toward a multiple of the flux quantum Φ₀ = h/2e. If the applied flux is close to half a flux quantum, then stable currents can flow counterclockwise to enhance the flux or clockwise to reduce it. These two supercurrent states can form the basis of a qubit.

In 2000, two research teams—James Lukens’s group at SUNY Stony Brook ⁵ and a collaboration between Hans Mooij and coworkers at Delft University of Technology and Terry Orlando, Seth Lloyd, and colleagues at MIT ⁶ —demonstrated spectroscopically the superposition of macroscopic current states of opposite polarity. Currents of half a microampere flowed clockwise and counterclockwise simultaneously in the Delft-MIT experiments. Opposing currents up to a few microamperes were found in the Stony Brook work. Although those results represent a first step toward implementing a qubit, coherent oscillations and control of the superposed states have yet to be demonstrated in such flux-based circuits.

Tuning out the noise

The new qubit design in the Saclay experiments, illustrated in 1, was in a regime in which the energy states of the system could not be simply described in terms of either the charge of the Cooper-pair box or the phase of the superconducting island. Nevertheless, the energy states depended on both the applied gate voltage and the applied magnetic flux that threaded the loop formed by the Cooper-pair box, its two isolating small Josephson junctions, and a large shunting Josephson junction. Indeed, by tweaking the applied voltage and flux, the researchers could tune the system to an optimal working point in which the energy levels were largely insensitive both to charge noise and to flux noise.

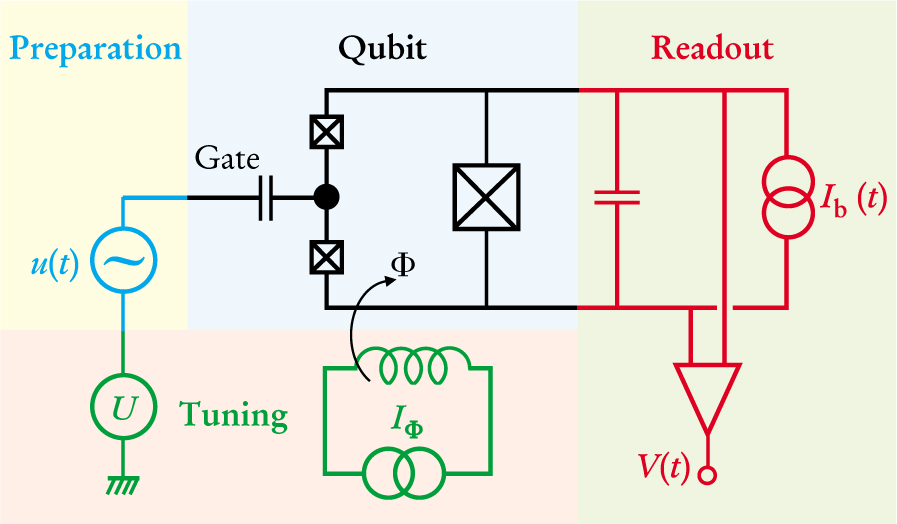
At this optimal point, the two qubit states had the same average charge, and each produced no net circulating current. “The system is as inconspicuous as possible,” explains the Saclay group’s Michel Devoret (now at Yale University). “Not letting the environment know what state you’re in maximizes the coherence time.”

The Saclay design also resulted in improved detection of the qubit state, compared with earlier efforts. To measure the state of the qubit, the researchers applied a bias-current pulse through the Cooper-pair box and the shunting Josephson junction. During the rise of the pulse, an additional supercurrent developed around the qubit loop in a direction dependent on the qubit state: counterclockwise for state |0>, which reduces the current through the shunting junction, and clockwise for state |1>, which increases the current through the shunt. Consequently, if the qubit was in the excited state, the total current through the shunt exceeded its critical current, producing a finite, measurable voltage.

“The Saclay group demonstrated nearly single-shot readout of the qubit,” notes Nakamura. “Although the efficiency was not as high as expected, that is a quite remarkable achievement.”

Figure 2 shows the coherent evolution of the Saclay qubit as revealed in a so-called Ramsey fringe experiment. Using a microwave pulse resonant with the energy splitting between the qubit’s two states, the researchers prepared the qubit in a coherent superposition. After waiting for a time Δt, during which the qubit evolved freely, the researchers applied a second pulse and then measured the qubit state. The coherence time determined from the experiment was 0.5 µs, two orders of magnitude longer than the coherence time in the earlier NEC experiments.

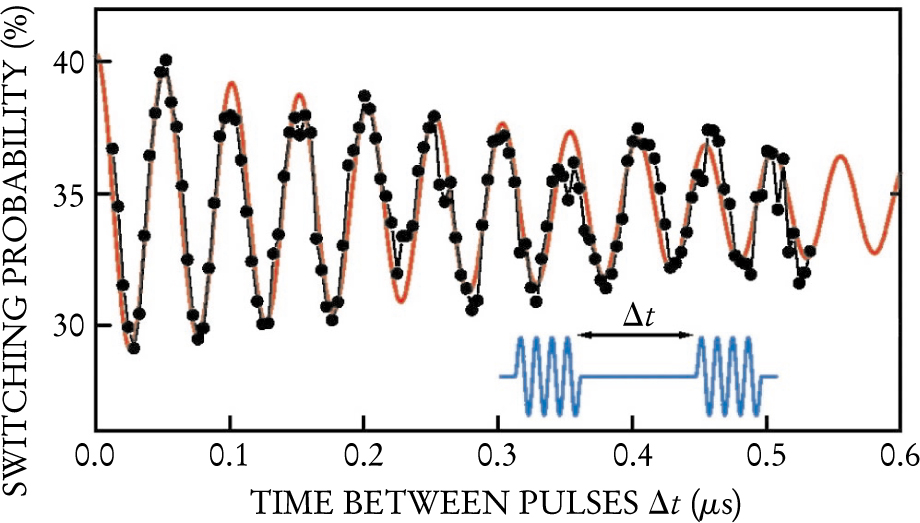
“With complete control of the state of our two-level system and the ability to measure it in a separate step, we think our qubit can really be used for developing solid-state two-qubit gates,” says Saclay’s Denis Vion.

A single Josephson junction

The qubit design of the Kansas group involved neither a Cooper-pair box nor a SQUID, but was instead based on a single Josephson junction. In 1985, John Martinis, Devoret, and John Clarke at the University of California, Berkeley, demonstrated the existence of quantum states within a single junction. ⁷ The potential energy landscape of the junction, considered as a function of the phase difference across it, is often modeled by the so-called “tilted washboard potential” illustrated in 3. The peaks and valleys arise from the cosinusoidal Josephson coupling energy and the tilt from a finite bias current. Within this potential, the phase of the junction behaves like a particle with a mass proportional to the junction’s capacitance.

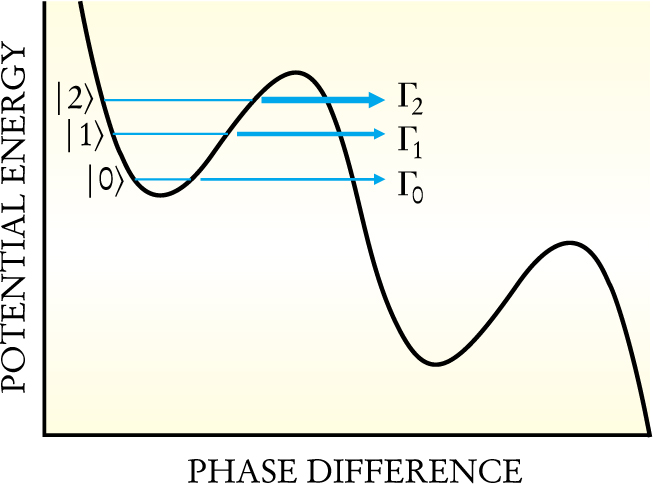
For bias currents below the junction’s critical current, the potential energy has a series of local minima differing in phase by 2π. Within each of these wells, the energy levels are quantized. Han and coworkers ² at Kansas have recently demonstrated coherent oscillations of a qubit, formed from the lowest two energy levels, with a coherence time in the presence of a resonant field on the order of 5 µs. And at the 2002 March meeting of the American Physical Society in Indianapolis, Indiana, Martinis (now at NIST in Boulder, Colorado) reported a similar qubit implementation that could be measured with high single-shot efficiency.

The large Josephson junctions in these experiments—10 µm × 10µm— have low impedances, which makes them particularly vulnerable to environmental decoherence. The Kansas researchers overcame this obstacle by placing their junction in a microstrip resonator that served to isolate the junction from the environment.

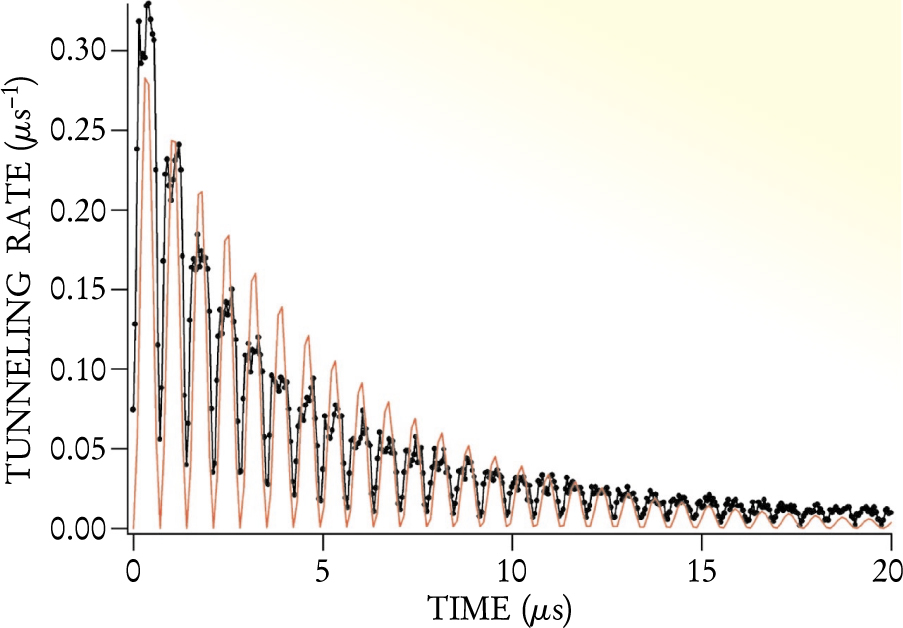
Microwaves with a frequency closely matched to the qubit level spacing produced so-called Rabi oscillations— coherent oscillations between the two energy states. To measure the state of the qubit, Han and coworkers relied on the metastability of the phase states in the potential well. The probability that the phase will tunnel quantum mechanically out of the potential well is about three orders of magnitude higher for a well’s first excited state than for its ground state. The observed tunneling rate is therefore essentially proportional to the occupation of the excited state. Using a timer with subnanosecond accuracy, the researchers were thus able to follow the Rabi oscillations of the qubit over several microseconds (4).

Due to the stochastic, passive nature of the measurement process, the Kansas experiments had to be repeated 10⁴ to 10⁵ times. Martinis and col leagues at NIST, collaborating with Cristian Urbina of the Quantronics group, have reported an active detection scheme that’s much more efficient: They applied a second microwave pulse tuned to drive a transition from the first to the second excited state. The tunneling rate from the second excited state was yet another three orders of magnitude larger, and so the system rapidly entered a finite-voltage state if it was in state |1> before the probe pulse. The team inferred a single-shot measurement fidelity of 85% with this technique. But although they carefully designed a high-impedance circuit to protect their junction from the environment, the NIST researchers observed a coherence time of only tens of nanoseconds in their junction, which they attribute to junction imperfections.

The long coherence times demonstrated in both the Saclay and the single-junction circuit geometries are getting closer to a target benchmark of allowing 10⁴ quantum manipulations (each occurring on the scale of the Rabi oscillation period, typically 1 nanosecond or longer) before decoherence sets in. In addition to further work to identify decoherence sources and reduce their effects, many research groups are already starting to plan their attack on the next step: coupling two or more superconducting qubits together.