Two groups measure the quasiparticle charge of the $\frac{5}{2}$ fractional quantum Hall state

The defining characteristic of the fractional quantum Hall effect is outwardly simple: At low enough temperatures and high enough magnetic fields, and in clean enough samples, the Hall conductance as a function of magnetic field features plateaus at exact rational fractions of e ²/h.

When Daniel Tsui, Horst Stormer, and Arthur Gossard first discovered the effect in 1981, all the fractions they found had odd denominators: $\frac{1}{3}$ , $\frac{2}{5}$ , $\frac{3}{7}$ , … $\frac{2}{3}$ , $\frac{3}{5}$ , $\frac{4}{7}$ , …, and so on. Within a year Robert Laughlin had devised his famous wavefunction that encapsulates the many-body interactions responsible for the effect.

Then in 1986 Stormer’s graduate student Robert Willett discovered an even-denominator plateau at $\frac{5}{2}$ . The need to go beyond Laughlin’s wavefunction was immediately clear. Because electrons obey Fermi–Dirac statistics, any wavefunction that describes them must be antisymmetric under particle exchange. To meet that condition, Laughlin’s wavefunction, which features the Hall state denominator as an exponent, requires the denominator to be odd.

Two years before Willett’s discovery, Bertrand Halperin had explored the possibility of even-denominator states. They’d be possible, he theorized, if the electrons paired up and changed their statistics to Bose–Einstein and their wavefunction to symmetric.

Even the odd-denominator states, which lack pairing, are complex. Long-range entanglement among the strongly interacting electrons yields a liquidlike state whose excitations behave like quasiparticles of fractional charge. Pairing increases the complexity further. A full and general description of the fractional quantum Hall state remains elusive.

As if to evince the gap in understanding, there are currently six candidate wavefunctions for the $\frac{5}{2}$ state. Their names—Pfaffian, 331, U(1) × SU (2), to give three examples—reflect their characteristic mathematical features. But despite their diversity, all six candidates require the quasiparticles to have a charge of e/4.

Reassuringly for the candidates’ proponents, that value has now been confirmed by two groups of experimenters: one led by Mordechai Heiblum of the Weizmann Institute of Science in Rehovot, Israel; ¹ the other led by Charles Marcus of Harvard University and Marc Kastner of MIT. ²

Both teams made use of tunneling between the edges of a Hall bar, but their experiments are different and complementary. The Weizmann researchers derived the quasiparticle charge e ^* directly by measuring shot noise. The method used by the Harvard–MIT researchers was somewhat less direct in that it relied on a model developed by MIT’s Xiao-Gang Wen. But in addition to e ^*, the Harvard–MIT method also yielded g, an exponent that embodies the quasiparticles’ statistics and can discriminate among candidate wavefunctions.

The value of g obtained by the Harvard–MIT team is somewhat imprecise, but the two wavefunctions most compatible with the result have an exotic and interesting property: They are nonabelian. Operations that exchange particles within a nonabelian state don’t commute.

Finding a nonabelian state of matter would be a coup in its own right. The rich and subtle physics of such states would provide an arena where theoretical ideas from particle physics and condensed matter could be combined, extended, and tested.

There’s another reason for anticipated excitement. Swapping nonabelian particles doesn’t merely add a phase, as is the case for electrons, photons, or other abelian particles. Rather, a swap would transform one collective ground state into another via a unitary operation akin to flipping qubits. Because the operation involves the entire collective, it’s immune to the local perturbations that bedevil many other proposals for manipulating qubits. A nonabelian $\frac{5}{2}$ state could serve as a platform for so-called topological quantum computation (see Physics Today, October 2005, page 21 , and July 2006, page 32 ).

Verifying the nonabelian nature of the $\frac{5}{2}$ state is a necessary step toward exploiting the state for topological quantum computation. Other, formidable steps remain. But in measuring the quasiparticle charge, the Weizmann and Harvard–MIT teams have already built some of the device structures needed to reach that goal.

The fractions that characterize the conductance plateaus correspond to and have the same value as the filling factor v (the number of electrons divided by the number of magnetic flux quanta). How electrons behave when v = $\frac{5}{2}$ or any other rational fraction depends on where they are in the Hall bar.

In the bar’s central bulk, the strong magnetic field traps conduction-band electrons in tight cyclotron orbits. Unable to move except in circles, the electrons can’t transport charge. The bulk is an insulator. At the bar’s edges, the electrons can’t complete their cyclotron orbits; they transport charge in counter-propagating edge states. And they do so as if split into fractionally charged quasiparticles.

Thanks to the Pauli exclusion principle, the quasiparticles flowing in the edge states keep apart like disciplined soldiers on a march. The resulting current is free of statistical, or shot, noise. If you could route the quasiparticles through a turnstile as they passed along the edges, the clicks would be rhythmic and regular.

Shot-noise measurements rely on simultaneously measuring fluctuations, which depend on the number of charged particles, and the current, which depends on the number of charged particles and their charge. At fixed current, the higher the particle charge becomes the lower the particle number needed and the higher the noise. In the hypothetical turnstile, the higher the charge, the sparser and more irregular the clicks would be.

But if edge currents are noiseless, how can one use shot noise to determine the quasiparticle charge? The answer is to pinch the edge currents together so that tunneling can take place between them. When a quasiparticle hops randomly across from one edge to the other, the gap it leaves behind in the orderly train of charge behaves like a source of shot noise.

Conceivably, one could bring the edge currents together by fashioning a Hall bar into an hourglass shape, but it’s more effective to do so electrostatically with a quantum point contact. The QPC consists of two sharp, closely spaced electrodes deposited on top of the Hall bar. Applying a strong negative voltage to the electrodes effectively clears away electrons from the region beneath the electrodes, effectively cutting the bar in two. Easing the voltage a bit creates a narrow isthmus, as shown in figure 1.

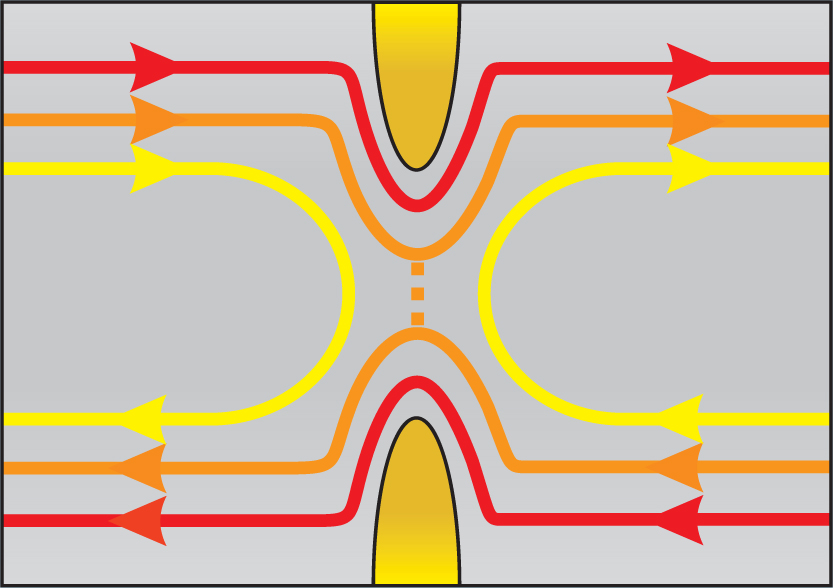
One consequence of using a QPC is that depleting the electrons at the isthmus changes the local density of electrons. If the applied magnetic field puts the bulk into, say, the v = 3 Hall state, the electrons that flow in edge states at the opening of the QPC could be in the lower $\frac{7}{3}$ state. Indeed, the QPC’s size and voltage are such that several edge states of different values of v can coexist from, say, $\frac{8}{3}$ at the center of the QPC, through $\frac{5}{2}$ , to $\frac{7}{3}$ on the outside. Identifying which edge state participates in the tunneling was crucial to the success of the Weizmann experiment.

In Rehovot

Besides Heiblum, the Weizmann team consists of Heiblum’s graduate student Merav Dolev, who did the experiment; Vladimir Umansky, who made the highly pure heterostructure needed for the experiment; theorist Ady Stern; and Diana Mahalu, who patterned the device. Umansky’s role is noteworthy. Until now, from Willett’s 1986 discovery on, Bell Labs remained the world’s only source of heterostructures clean enough to sustain the fragile $\frac{5}{2}$ state.

For the task of identifying the edge states, Dolev made use of observations of how the transmission through the device varied with the total, longitudinal current. When the QPC is wide open and when the bulk is in, say, the v = 3 state, no tunneling occurs and the conductance is 3e ²/h, regardless of current.

Narrowing the QPC starts to bring the lower-lying edge states, v = $\frac{8}{3}$ , $\frac{5}{2}$ , $\frac{7}{3}$ , and so on, into play and raises the probability for tunneling across. As a result, the transmission starts to drop. At the same time, the transmission acquires a dependence on current.

Crucially, the current dependence disappears whenever the QPC is tuned to exclude tunneling—that is, to accommodate edge states that either pass through intact or are completely reflected. That case would correspond to a figure 1 without the orange, tunneling current. Measuring the Hall conductance at that point would identify the lowest-lying red current and, by implication, the next highest current.

Although the transmission dependence is not fully accounted for by theory, it is experimentally reproducible and qualitatively understood. Dolev used the dependence to tune the device and to make sure that the $\frac{5}{2}$ edge state is the one that tunnels across. The lower-lying $\frac{8}{3}$ state doesn’t contribute to the noise, but its share of the current has to be removed from the formula for calculating the noise of the $\frac{5}{2}$ state.

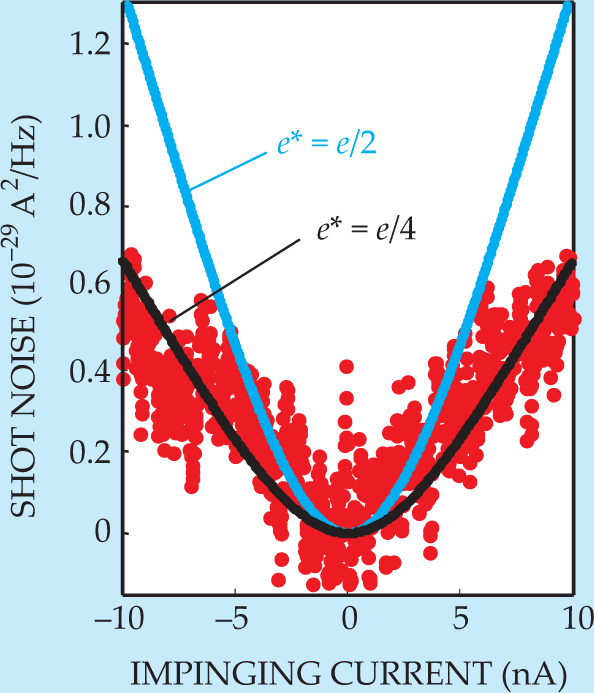
Figure 2 shows the results of one run. The plot of noise versus current is consistent with a quasiparticle charge of e/4. Although all the present candidates for the true $\frac{5}{2}$ wavefunction feature e/4 quasiparticles, the quasiparticles in some yet-to-be conceived alternative could be so tightly paired that they behave like e/2 particles. That possibility is clearly ruled out.

In Cambridge

The Harvard–MIT team consists of Marcus and Kastner, plus Marcus’s postdoc Jeffrey Miller and Kastner’s graduate student Iuliana Radu. Miller and Radu made the device and did the experiment. Loren Pfeiffer and Kenneth West of Bell Labs provided the heterostructure.

Like their Weizmann counterparts, Miller and Radu worried about which states were present in the QPC. By luck, they happened on a way of annealing their device to ensure that the edge states in the bulk and in the QPC were the same.

Miller and Radu would usually turn on the QPC gates after cooling the Hall bar to its few-millikelvin operating temperature. That sequence causes the electron density and therefore v, to be lower in the QPC than in the bulk. But one day for some now-forgotten reason, they reversed the sequence. That gave dopants in the heterostructure the chance to equilibrate before the lower temperature froze them in place. The upshot was to preserve the same electron density in the bulk as in the QPC.

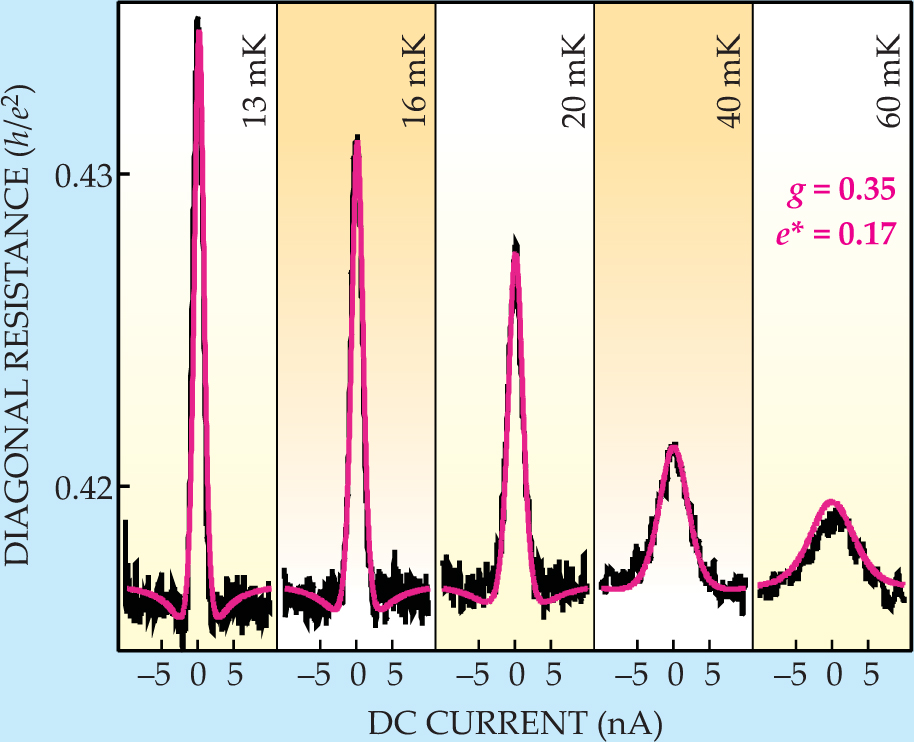
To derive the quasiparticle charge and the exponent g, Miller and Radu measured the resistance as a function of temperature. According to Wen’s theory, the resistance reaches a peak at zero bias and falls off with increasing current. The peak’s width is proportional to the temperature divided by the charge of the tunneling quasiparticles, whereas the peak’s height is proportional to the temperature raised to the power of 2g – 2. No other adjustable parameters appear in Wen’s formula. Fitting all the traces at five different temperatures yielded a quasiparticle charge e ^* of 0.17 and a g of 0.35. Figure 3 shows the fit.

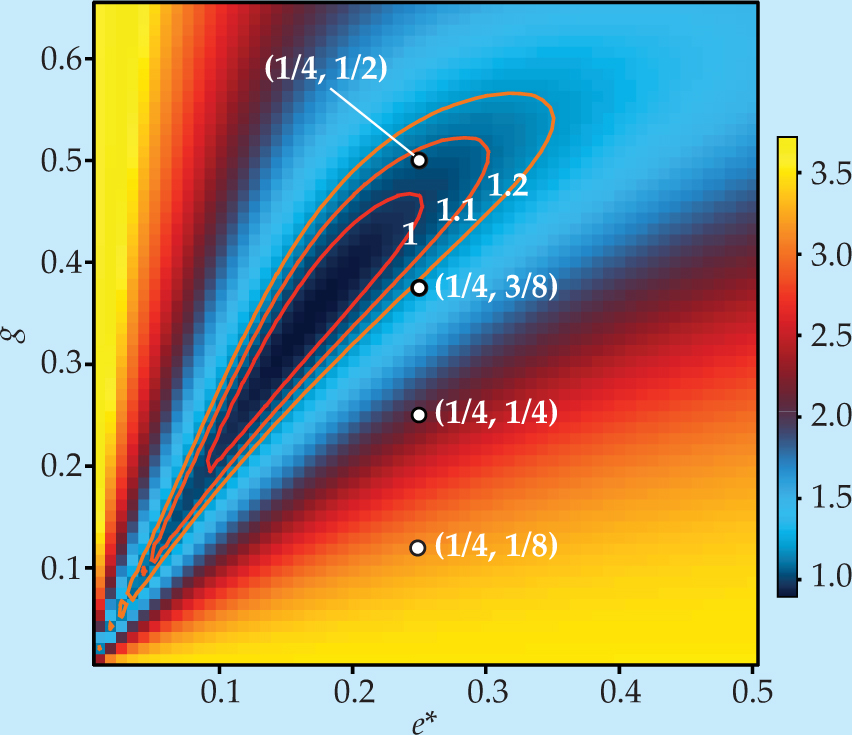
Each of the candidate wavefunctions predicts a not necessarily unique pair of e ^* and g. How close those predictions come to experiment is shown in figure 4. The best-fitting pair is ( $\frac{1}{4}$ , $\frac{1}{2}$ ), which is shared by two nonabelian wavefunctions, anti-Pfaffian and U(1) × SU (2). But the next best, and still acceptable, pair, ( $\frac{1}{4}$ , $\frac{3}{8}$ ), belongs to the abelian 331 state.

Verifying the nonabelian nature of the $\frac{5}{2}$ state requires a multi-QPC device that creates interference between quasiparticles. Building such a device constitutes the next step. It will not be easy, but both Heiblum and Marcus are reassured that the $\frac{5}{2}$ state is not so fragile that it falls apart when squeezed by gate voltages.

“We all have the information,” says Marcus. “It would be perverse delayed gratification to do anything right now other than interference experiments.”