The early universe in a quantum gas
DOI: 10.1063/PT.3.5152
To look back in time, astronomers and cosmologists need only look to the skies: When they view an object a million light-years away, they’re seeing it as it existed a million years ago. That approach, however, hits a wall at the cosmic microwave background (CMB), which dates to 380 000 years after the Big Bang. Before that, the universe was filled with dense plasma, which was electromagnetically opaque.
Theorists have proposed that the very early universe experienced a so-called inflationary epoch, in which it doubled in size some 100 times in less than 10−30 of a second before the expansion abruptly slowed. (The universe is still expanding, and the expansion is accelerating, but nowhere near as speedily as it was then.) Confirming or refuting inflation theory, however, is challenging, because the only universe we can observe is the one we live in. Cosmologists can’t run experiments to compare what did happen with all the other things that might have happened.
But it may be possible to mimic at least some of the physics of the early universe in another system that does lend itself to experiments. Heidelberg University’s Markus Oberthaler, his PhD student Celia Viermann, and their colleagues are doing just that with their experiments on a pancake-shaped Bose–Einstein condensate (BEC) of potassium atoms. 1 Their goal is to study how quantum fields may have behaved in a rapidly expanding spacetime—and what imprints inflation may have left on the observable universe for eons to come. And they do it all without changing the physical size of their BEC.
Microwave fluctuations
Even though the CMB didn’t originate until hundreds of thousands of years after the inflationary epoch, it offers some of the most suggestive evidence that inflation happened at all. Figure
Figure 1.

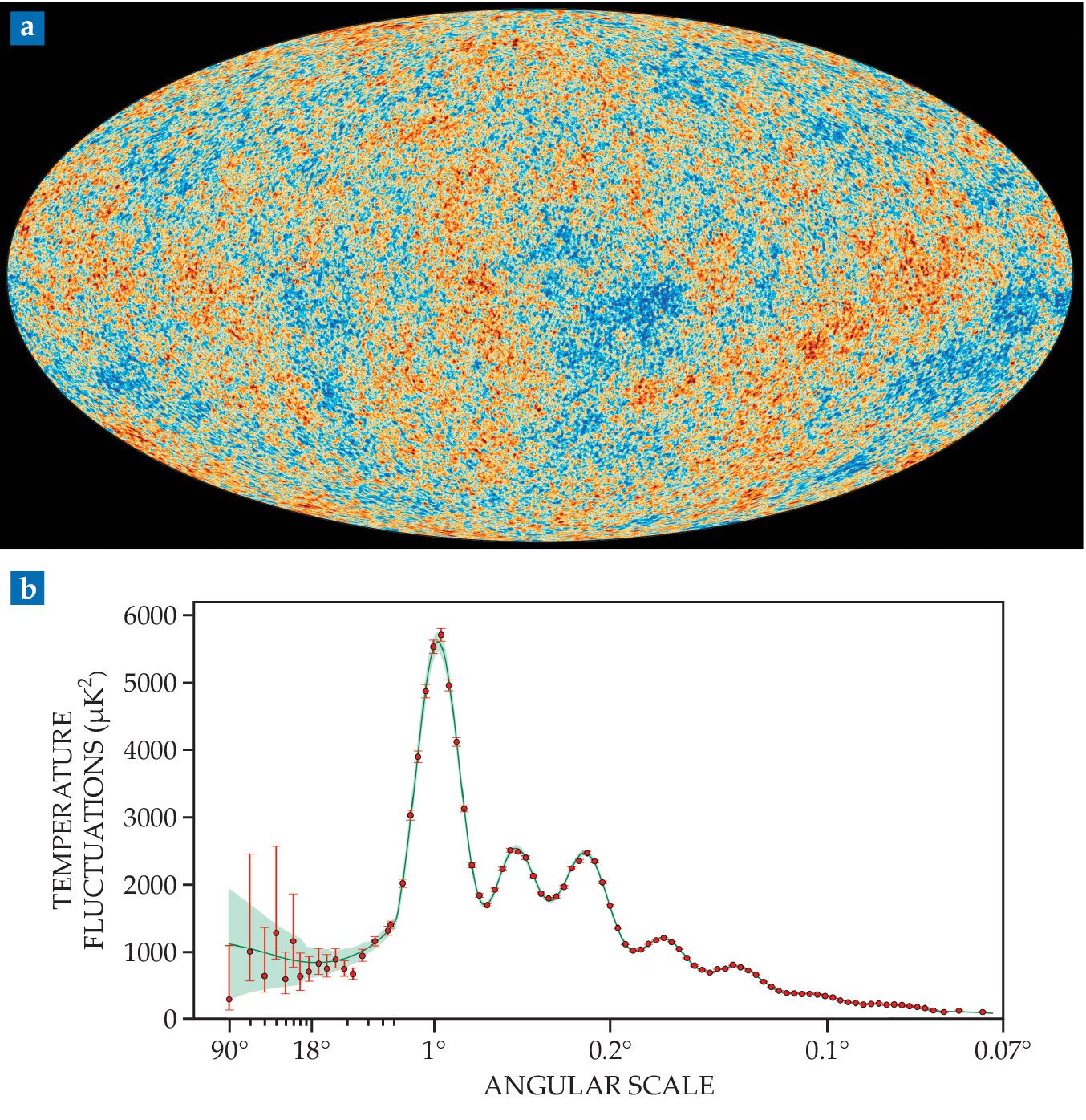
The cosmic microwave background (a), as observed by the Planck spacecraft, looks almost the same in every direction. Its minuscule temperature fluctuations, shown in red and blue here, are evidence of cosmic sound waves that propagated through the early universe. (b) When broken down by angular size on the sky, the fluctuation data (red) generally agree well with the predictions of cosmological theory (green). At large angular scales, however, the comparison is hindered by irreducible cosmic variance—that is, the limited amount of data that can be extracted from one universe. (Both panels courtesy of the European Space Agency and the Planck Collaboration.)
How can that be? CMB photons arriving at Earth from opposite directions originated at opposite edges of the observable universe. When would those points ever have had time to exchange information with each other, let alone come to thermal equilibrium? Inflation offers a compelling answer: Just before the inflationary epoch, the theory posits, the whole of the observable universe was less than the size of a proton. It could have quickly equilibrated, then expanded so fast that its most distant points were pulled out of causal contact. That’s not the only possible answer (see the article by Robert Brandenberger, Physics Today, March 2008, page 44
A closer look at the CMB strengthens inflation’s predictive success. The temperature fluctuations in figure
For angular sizes of a few degrees and smaller, the model is an excellent fit to the data. But the agreement is shakier at larger scales. At the leftmost end of the plot, most of the red data points are on the low side of the green curve. But it’s hard to tell how much of the discrepancy is real and how much is a statistical anomaly, because the uncertainties are so large—a consequence of the fact that we have only one universe to study and only one sky to look at. Only a few 90° patches can fit on the sky, so any analysis of them is fundamentally limited in precision. In principle, more data could be gathered by observing the CMB from a different vantage point, perhaps a billion light-years away. But practically, that’s not going to happen any time soon.
Experimental simulations
By simulating inflationary-epoch physics in an experiment, Oberthaler and colleagues could help bypass such statistical limitations. Notably, they’re not trying to exactly reproduce the inflationary universe in all its complexity. Instead, they’re building an experimental platform for studying a quantum field in an expanding spacetime—a simplified model of the early universe, but one that’s still difficult to solve theoretically.
Researchers have taken a similar approach in using quantum gases to simulate other mysterious systems, such as high-temperature superconductors. (See Physics Today, August 2017, page 17
Reducing the whole universe to a single field isn’t as gross a simplification as one might think. According to inflation theory, the universe didn’t begin the inflationary epoch with all the matter and energy that exists today packed into a space smaller than a proton. Rather, the inflationary-epoch universe was largely empty, apart from a field, called the inflaton, whose quantum fluctuations eventually gave rise to all the complexity we see today.
The inflaton would have been a scalar field, meaning that its quanta were spin-zero bosons. (In the standard model of particle physics, the only fundamental spin-zero boson is the Higgs particle; it’s possible, but not certain, that the inflaton and Higgs fields were one and the same.) Because of its bosonic character, it’s reasonably well simulated by a BEC.
But how can one study a BEC in expanding spacetime? One way, pursued recently by Gretchen Campbell and colleagues at the Joint Quantum Institute and the University of Maryland, College Park, is to physically expand the BEC. 2 Another way is to tinker with the interatomic interactions to make the BEC behave as if it’s expanding, even though it’s not. That’s the approach that Oberthaler and colleagues used.
As a thought experiment, imagine that your body and all the objects around you were suddenly halved in size. Your arms could reach only half as far as before, and it would take twice as long to walk anywhere. It would seem as though space itself were twice as big.
To manipulate their BEC atoms’ reach, the Heidelberg researchers applied a magnetic field in the vicinity of what’s known as a Feshbach resonance. At the resonance exactly, 561 G for potassium atoms, the atoms’ reach diverges, and they behave as if they’re infinitesimally close together. Away from the resonance, their reach shrinks, and the effective space grows. In practice, if the field is tuned too close to the resonance, the atoms interact so strongly that they knock one another out of the condensate. To be on the safe side, the researchers ramped the field from 557 G to 540 G, which is enough to inflate the BEC universe by about a factor of three.
Postinflation oscillations
A simple prediction of quantum field theory is that in an expanding universe, a scalar field picks up quantum fluctuations that produce particle–antiparticle pairs, whereas in a static universe, it doesn’t. In an expanding BEC, the particles produced would be phonons; the same physics is expected to describe how real particles emerged from quantum fluctuations in the early universe.
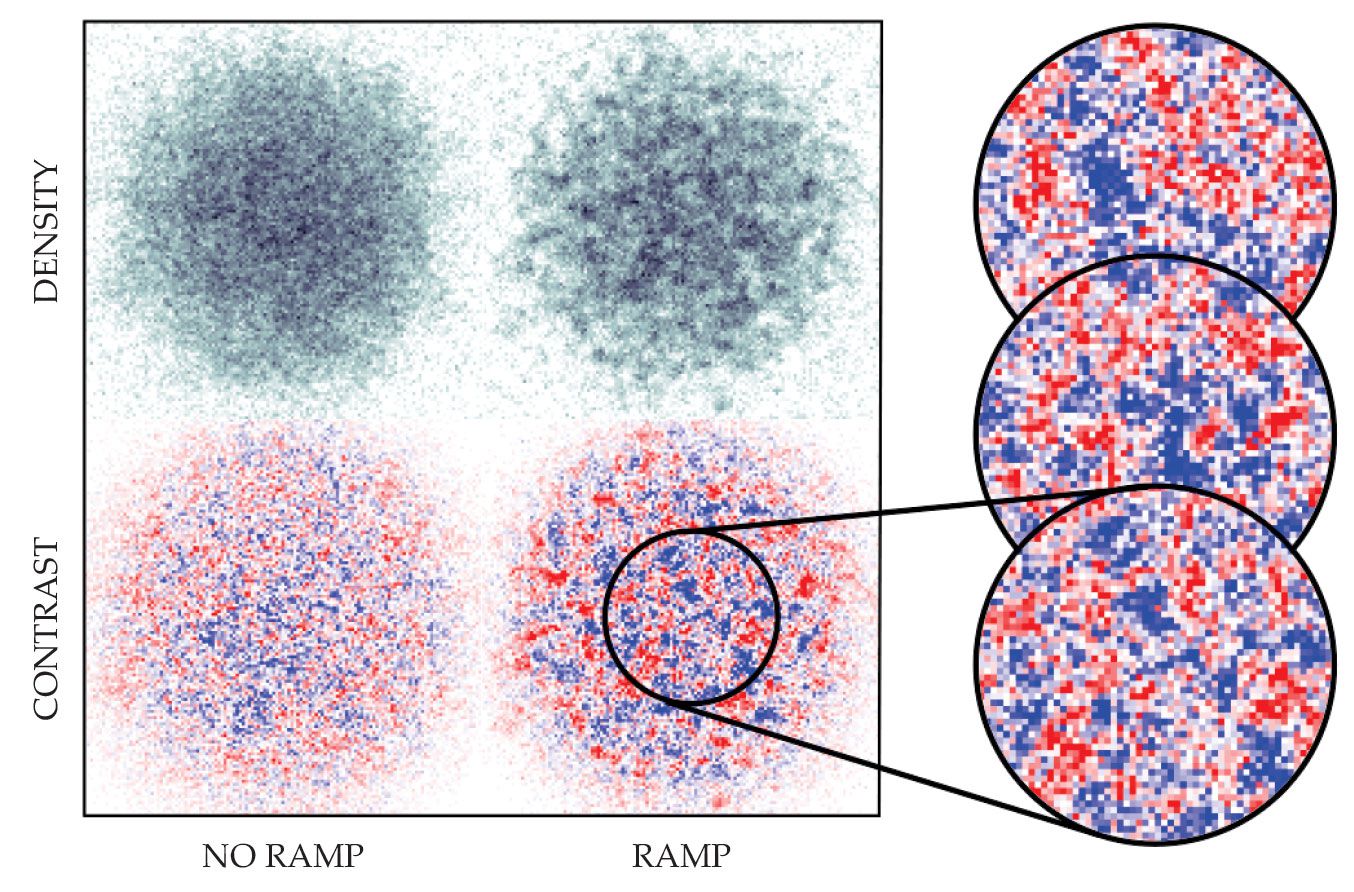
The predicted particle production is borne out by the results shown in figure
Figure 2.

By ramping a magnetic field in the vicinity of a so-called Feshbach resonance, researchers trick a Bose–Einstein condensate into behaving like the expanding early universe—even though the condensate’s physical size remains the same. Under the ramped field, the condensate picks up density fluctuations; in the early universe, such quantum field fluctuations became particle–antiparticle pairs. The cutouts at right show how additional data can be gathered by repeating the experiment. (Adapted from ref.
The qualitative dynamics of a Feshbach-resonance expanding universe were observed a decade ago by the University of Chicago’s Cheng Chin and colleagues. 3 Those researchers looked at the effects of a step change in the magnetic field—an instantaneous, unmeasurably fast expansion. In contrast, Oberthaler and colleagues, in collaboration with the theorist Stefan Floerchinger, wanted to take the investigation a step deeper: What is the effect of inflation’s functional form? Would different inflation profiles leave differing imprints on the simulated universe that could be observable long after the inflationary epoch was over?
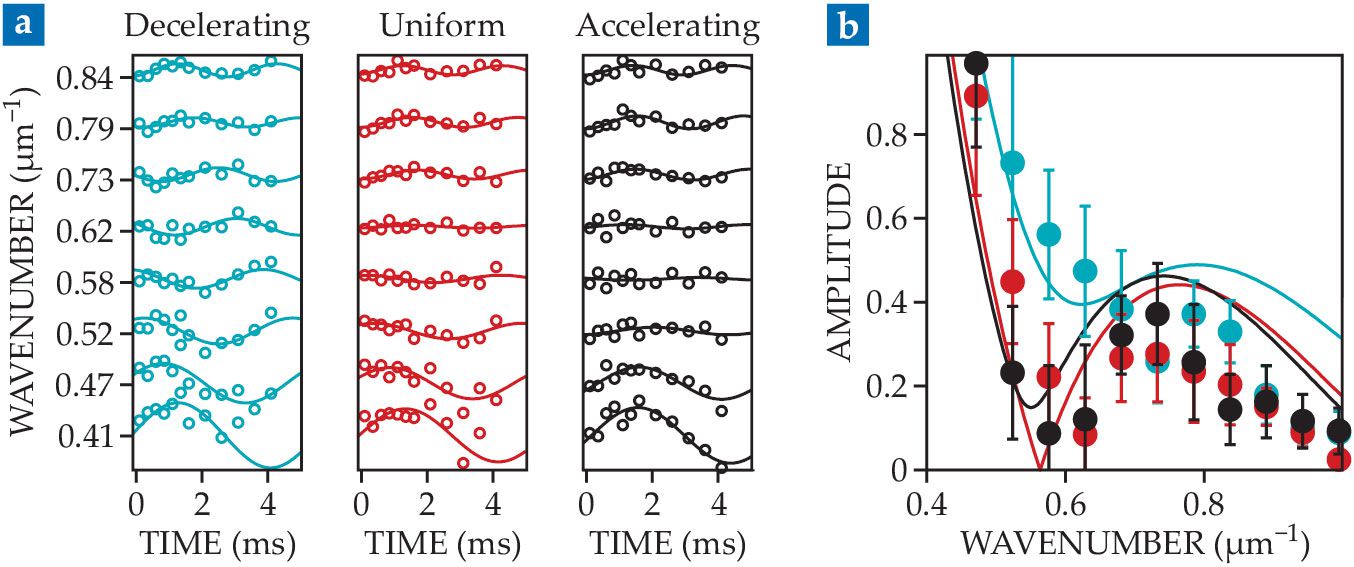
To find out, they experimentally tested three different expansion histories: one that decelerated, one with uniform speed, and one that accelerated. (None of the three mimicked the exponential expansion of cosmic inflation; even the accelerating-expansion experiment followed a power law.) In all three cases, after the expansion was finished, the researchers saw the BEC fill with acoustic waves, similar to the ones that permeated the real universe during the plasma epoch and led to the temperature fluctuations in the CMB.
But whereas the CMB gives only a one-time snapshot of the cosmos, Oberthaler and colleagues can track the BEC waves in real time and break them down by wavenumber, as shown in figure
Figure 3.

Acoustic waves carry an imprint of a simulated universe’s expansion history that’s observable even after the expansion is over. (a) In the wake of three different expansion profiles—decelerating, uniform speed, and accelerating—the waves around a wavenumber of 0.6 µm−1 have different amplitudes. (b) The observations (data points in the same colors as panel a) agree well with theory (solid lines). (Adapted from ref.
Now that the researchers have confirmed that their BEC can reproduce what theory predicts, they hope to be able to use it to investigate questions that theory, until now, has left open. For example, what, if anything, happened before inflation? If the inflationary epoch left an observable mark on the universe today, is it possible that a preinflationary epoch did also? That’s an extremely ambitious question, but with an experiment that can probe the physics of an expanding universe in detail—including quantum fluctuations, correlations, entanglement, and thermalization—the researchers hope to make some headway.
References
1. C. Viermann et al., Nature 611, 260 (2022). https://doi.org/10.1038/s41586-022-05313-9
2. S. Eckel et al., Phys. Rev. X 8, 021021 (2018). https://doi.org/10.1103/PhysRevX.8.021021
3. C.-L. Hung, V. Gurarie, C. Chin, Science 341, 1213 (2013). https://doi.org/10.1126/science.1237557
More about the authors
Johanna L. Miller, jmiller@aip.org




