Statistical mechanics elucidates constraints on the ultimate accuracy of biochemical sensing

In biology textbooks , the way proteins work is often depicted by what looks like a set of puzzle pieces. A small piece, a regulator molecule, say, fits into a large piece, an enzyme, say. The enzyme’s shape then changes to one that fits snugly around a medium-sized piece, the enzyme’s substrate.

Those cartoons are meant to convey the exquisite specificity of biochemical reactions. Of the myriad reactions inside a cell, a given enzyme catalyzes just one. Not surprisingly, the picture doesn’t tell the whole story. What’s missing is the physical setting.

“In the world of a cell as small as a bacterium,” wrote Howard Berg and Edward Purcell in a classic 1977 paper, ¹ “transport of molecules is effected by diffusion, rather than bulk flow; movement is resisted by viscosity, not inertia; the energy of thermal fluctuation, kT, is large enough to perturb the cell’s motion.”

Under those conditions, the turning off of genes by transcription factors or the response to caffeine molecules of a neuron, just two examples, both resemble the sampling of a signal. Although the detector, the protein, responds more or less promptly to its target, fluctuations in its environment limit its accuracy.

Berg and Purcell derived an expression for how accurately a sensor of radius a can determine in time τ the mean concentration c of a target molecule whose diffusion coefficient is D: $$\Delta c/c={1/\left(Dac\tau \right)}^{1/2}.$$

Berg and Purcell’s analysis treated the sensor as a sticky sphere: Every target that hits the sensor sticks to it. But real proteins are like flexible scaffolds that fluctuate between two or more metastable configurations. And real target molecules bind and unbind at different kinetic rates.

In 2005 William Bialek of Princeton University and Sima Setayeshgar of Indiana University incorporated those complications into a reanalysis of limiting sensitivity. Metastability and kinetics, they found, contribute an additional, always positive term to Δc/c. Berg and Purcell’s expression can therefore be thought of as a noise floor: Real systems are less accurate than Berg and Purcell’s model; they can never be more accurate. ²

Now, Bialek and Setayeshgar have taken a further step toward accounting for the complexities of real biomolecular sensors: cooperativity. ³ A cooperative biomolecule consists of two or more identical subunits arranged symmetrically. The binding of one target molecule to one subunit alters the molecule’s configuration and makes binding a second target more favorable. The more subunits a molecule contains, the greater the cooperative boost to binding.

Human hemoglobin, whose job is to scoop up oxygen and ferry it to cells that need it, has four subunits. Cooperative interactions among them result in a steep dependence of the fraction of occupied binding sites on the ambient oxygen concentration. In sensor proteins, cooperative interactions enhance sensitivity. Even a tiny change in concentration will boost the average number of sensors in a particular state. But can cooperative gain, which, in principle, is arbitrarily high, overcome background noise?

To answer that question, Bialek and Setayeshgar applied the fluctuation—dissipation theorem, as they did for their 2005 analysis. According to the theorem, a system in thermodynamic equilibrium will respond in the same way both to a small driving force and to a random thermal fluctuation. From that intuitive proposition, Albert Einstein famously related the dissipative, Brownian motion of a particle to the random, fluctuating knocks the particle receives from the molecules that surround it.

In Bialek and Setayeshgar’s analysis, the fluctuations come from the local concentration of target molecules as they bind and unbind, knocking the cooperative molecule dissipatively in and out of its various states.

Their analysis is somewhat involved, but, to Bialek and Setayeshgar’s surprise, it yielded a compact formula for Δc/c. As in their earlier 2005 analysis, including cooperativity adds a second, always positive term. Moreover, the formula is general: It applies to cooperative and noncooperative sensors alike. Whereas cooperativity increases the gain, it doesn’t lower the noise floor.

Experiments that determine Δc/c have been done only recently. According to Bialek and Setayeshgar’s formula, the 10% accuracy with which Escherichia coli transcribes genes is reached within one minute. That sampling time is consistent with the time, three minutes, that messenger RNA survives in the cell.

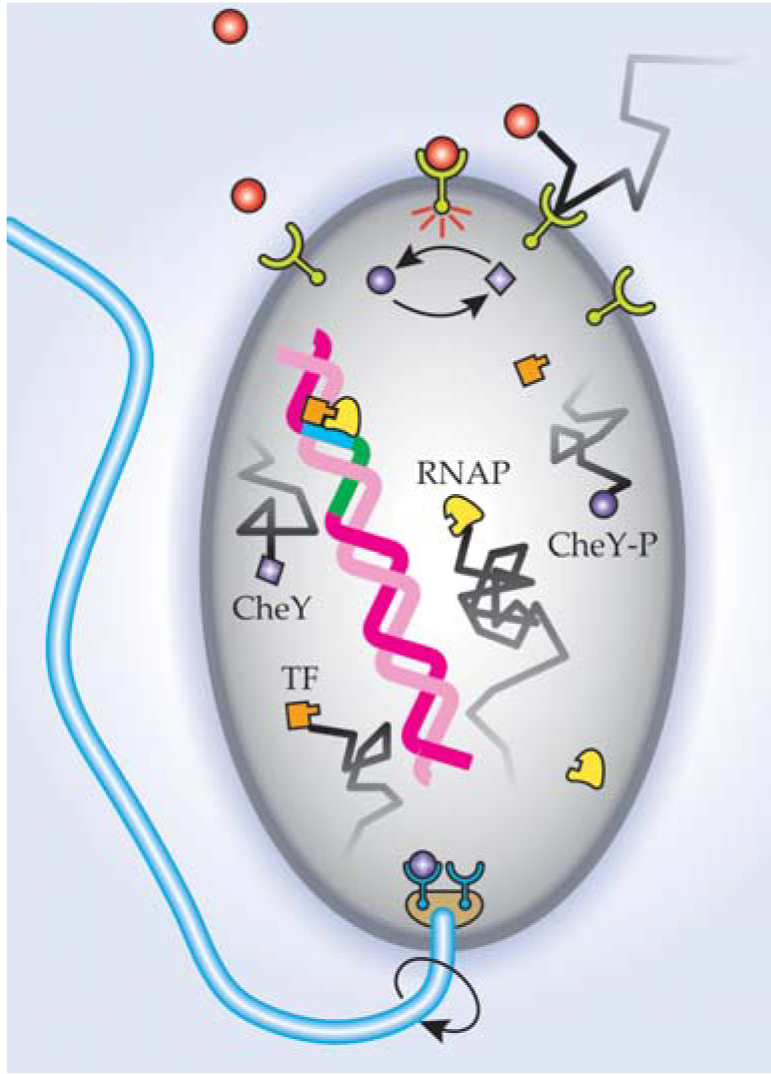
Bialek and Setayeshgar’s formula also predicts, within a factor of three, how often E. coli changes direction in response to concentration gradients (see figure). The agreement is historically apt. Purcell first became interested in biochemical sensing when he saw Berg’s movies of zigzagging bacteria.