Optical-lattice clock sets new standard for timekeeping
DOI: 10.1063/PT.3.2294
The basic protocol for quantum time metrology hasn’t changed much since 1955, the year of the atomic clock’s debut: Isolate an atom from external fields, tune coherent radiation to an atomic transition, and count the radiation’s oscillations to measure the ticking of time. (See the article by James Bergquist, Steven Jefferts, and David Wineland in Physics Today, March 2001, page 37
In practice, however, our abilities to isolate atoms and pinpoint their transition frequencies are imperfect. Even in the most careful experiments, environmental influences—stray radiation, interactions between atoms, and the like—inevitably perturb an atom’s internal state. Likewise, atoms’ thermal motion generates Doppler shifts that broaden spectral lines and make exact transition frequencies difficult to locate. Even our ability to count has limits: Until a couple of decades ago, atomic clocks were based on microwave hyperfine transitions, despite the broad relative linewidths, because electronic counters couldn’t keep up with higher-frequency radiation.
Nowadays, frequency combs can lock electronic counters with optical-frequency radiation, ion traps can isolate single atoms at a time, and laser cooling can slow those atoms to a virtual standstill. In 2001 researchers at NIST in Boulder, Colorado, combined all those elements to build an atomic clock based on a UV transition in a single, laser-cooled mercury ion.
1
Within a few years, single-ion optical clocks had become the world’s most accurate timekeepers. Today’s versions, able to measure time to within 1 part in 1017, are exquisite enough to detect the subtle gravity-induced time dilation due to a change in elevation of a fraction of a meter. (See Physics Today, November 2010, page 16
Over the past decade, several groups have been developing an alternative timekeeping strategy based not on measurements of single atoms but on measurements of ensembles of atoms trapped in optical lattices—arrays of traps formed by counterpropagating laser beams. Now one of those groups, led by Jun Ye (JILA, Boulder, Colorado), has succeeded in building an optical-lattice clock that outperforms the best existing single-ion clock. 2 So accurate is the new timepiece that it could run for nearly 5 billion years, more than the age of Earth, without missing a second.
Wavelength magic
The simplest way to set an atomic clock is to irradiate an atom with light of various frequencies and choose the frequency that most regularly induces the specified transition. To average out the statistical noise associated with detecting changes in the atom’s state, however, one needs to repeat the measurements many times over; the statistical uncertainty will fall roughly with the square root of the total number of measurements.
With single-ion clocks, those measurements are performed one atom at a time. In 2003 Hidetoshi Katori (University of Tokyo) and coworkers formally proposed a way to speed the process. 3 In the new strategy, thousands of neutral atoms would be laser-cooled, loaded into an optical lattice—each atom isolated in a separate potential well—and then probed simultaneously.
Unlike ion traps, optical lattices necessarily perturb the internal states of the atoms they trap; their trapping potential results from AC Stark shifts induced by the lattice light. Katori and other researchers—including Ye and Jeffrey Kimble of Caltech—had come up with a clever workaround for that problem: They showed how one could tune the lattice light to a “magic” wavelength, at which both atomic states involved in the clock transition are shifted by precisely the same energy. At that wavelength, the clock transition mimics one in an unperturbed atom. By 2006 a handful of groups, among them Katori’s and Ye’s, had used the magic-wavelength strategy to build the first generation of optical-lattice clocks.
Stability
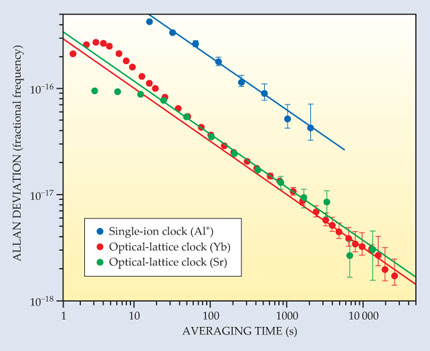
A good clock should be stable—the duration of its ticks shouldn’t vary over time. Quantum metrologists typically measure stability by running two clocks, based on the same transition, side by side. The fractional difference between the clocks’ tick rates is known as the Allan deviation. With single-ion clocks, it takes several minutes of averaging to reach an Allan deviation of 1 part in 1016. Optical-lattice clocks, because they measure thousands of atoms at once, can reach the same level in a matter of seconds.
Last fall a NIST group led by Andrew Ludlow ran two ytterbium optical-lattice clocks in an extended experiment to see how far the Allan deviation would fall. 4 In such an experiment, there’s no guarantee that the deviation will trend steadily downward: Frequency fluctuations of the lasers used to trap and probe the clock atoms can effectively place a ceiling on clock stability, as can subtle environmental changes such as temperature drifts. Using ultrastable lasers and carefully controlled experimental conditions, Ludlow and his team were able to keep those destabilizing factors largely in check. Their data, plotted in red in figure 1, show the Yb clocks reaching an Allan deviation of 1.6 × 10−18—a record low for clocks of any kind—after seven hours of averaging.
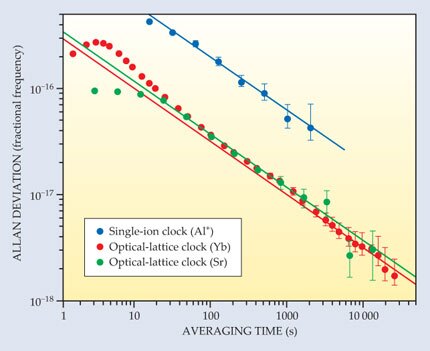
Figure 1. The Allan deviation, the fractional difference between two clocks’ tick rates, is a common measure of clock stability. The lower the deviation, the more stable the clocks. Here the Allan deviations of a pair of aluminum single-ion clocks (blue), a pair of ytterbium optical-lattice clocks (red), and a pair of strontium optical-lattice clocks (green) are plotted as a function of the measurement time used to determine their frequencies. The lines show the asymptotic trends. Optical-lattice clocks’ enhanced stability is due mainly to the noise reduction achieved by measuring many atoms at once. (Adapted from ref.
Accuracy
With their new clock, based on an optical transition in strontium, Ye and company can achieve stabilities comparable to those reached in the NIST experiment. For each measurement, a few thousand ultracold atoms are loaded into a one-dimensional optical lattice generated with a titanium:sapphire laser. Figure 2 shows the clock’s viewport; a cloud of trapped, fluorescing Sr atoms is seen in the center.

Figure 2. The strontium optical-lattice clock shown here is now the world’s most accurate timekeeper. Visible at the center is a cloud of trapped, fluorescing Sr atoms, used to determine the ticking frequency. Key to the clock’s accuracy is a temperature sensor (indicated by the green arrow), which is mounted on a retractable glass tube and used to characterize systematic errors caused by blackbody radiation. (Adapted from ref.

Stability doesn’t guarantee accuracy—even a clock that keeps consistent time may not keep the right time, as measured against the benchmark of a perfectly isolated atom. Stability does, however, play an important role: The ability to evaluate a clock’s systematic error is limited in part by the steadiness of its ticks. In the 1D lattice used by the Ye group, for example, multiple atoms often occupy the same potential well. To account for those atoms’ weak, but nonnegligible, interactions, the researchers must be able to detect subtle responses of the clock frequency to modulations in the number of trapped atoms.
The biggest source of systematic error in optical-lattice clocks is the blackbody radiation (BBR) shift, the energy shift due to the sensitivity of the clock atoms to thermal radiation from the surrounding apparatus. Atoms amenable to optical-lattice trapping tend to be much more susceptible to that shift than are the ions preferred for single-ion clocks.
To account for the BBR shift, one needs to determine the electric polarizability of the atoms and the radiation spectrum they see. To that end, Ye and company outfitted their clock with a retractable temperature sensor, indicated in figure 2 by the green arrow. Between frequency measurements, the sensor, coated with highly absorptive paint, can extend to measure the effective temperature of the radiation field at the position of the atoms and in the near vicinity. From the temperature, the researchers can calculate the corresponding radiation spectrum for an ideal blackbody; from its spatial gradients, they can estimate deviations from that ideal blackbody spectrum.
Combining the temperature information with a precise estimate of Sr’s electric polarizability, recently obtained by researchers at Physikalisch-Technische Bundesanstalt (NIST’s German counterpart), 5 Ye and company estimated the magnitude of the BBR shift with a fractional uncertainty of 4.1 × 10−18. Lesser sources of uncertainty—electrostatic fields due to charge heterogeneities along the viewports, interactions between atoms, and so forth—brought the total systematic uncertainty to 6.4 × 10−18. The previous record, held by an aluminum single-ion clock, was 8.6 × 10−18.
Ye thinks optical-lattice clocks can eventually reach a systematic uncertainty below 1 part in 1018. At that level, the atomic timepieces would provide stringent tests of the variability of physical constants, such as the fine-structure constant α that sets the strength of light–matter interactions. If α is changing over time, as some celestial observations have suggested, it should be evidenced by a drift in the ratios of different atomic transition frequencies. By comparing the ticking of Al+ and Hg+ ion clocks over the course of a year, 6 a NIST group led by James Bergquist has already established an upper bound on α’s annual variation at 1 part in 1017. A comparison between optical-lattice clocks may squeeze the upper limit further.
Ultrastable clocks might also function as quantum altimeters, capable of detecting centimeter changes in altitude based on the time-dilating effects of Earth’s gravitational potential. “Imagine you have a network of these clocks,” comments Ye. “You could measure in real time how a body of water is moving along Earth. Two clocks might allow you to see a gravitational wave coming from the deep universe. They would sort of be the ultimate quantum objects for measuring the spacetime fabric.”
References
1. S. A. Diddams et al., Science 293, 825 (2001). https://doi.org/10.1126/science.1061171
2. B. J. Bloom et al., Nature 506, 71 (2014). https://doi.org/10.1038/nature12941
3. H. Katori et al., Phys. Rev. Lett. 91, 173005 (2003). https://doi.org/10.1103/PhysRevLett.91.173005
4. N. Hinkley et al., Science 341, 1215 (2013). https://doi.org/10.1126/science.1240420
5. T. Middelmann et al., Phys. Rev. Lett. 109, 263004 (2012). https://doi.org/10.1103/PhysRevLett.109.263004
6. T. Rosenband et al., Science 319, 1808 (2008). https://doi.org/10.1126/science.1154622
7. C. W. Chou et al., Phys. Rev. Lett. 104, 070802 (2010). https://doi.org/10.1103/PhysRevLett.104.070802




