Light exhibits a spin hall effect
DOI: 10.1063/1.2911165
Applying an electric field along a frigid strip of near-defect-free semiconductor can drive a lateral imbalance of spin-up and spin-down electrons, a spin Hall effect. The effect, which comes in several varieties, depends at heart on the coupling between the electrons’ spin and orbital angular momentum (see Physics Today, February 2005, page 17
Light can have both spin—in the form of circular polarization—and orbital angular momentum or helixity. Could coupling between the two momenta engender a spin Hall effect for light? As Onur Hosten of the University of Illinois at Urbana-Champaign and his thesis adviser Paul Kwiat demonstrate in a new experiment, the answer is yes. 1
In the Illinois experiment, the role of the electric field was played by a step-wise gradient in refractive index. The role of spin-up and spin-down electrons was played by light’s right-hand and left-hand components of circular polarization. The effect itself appeared as a tiny lateral separation of the two circularly polarized components as they passed at an angle from air into glass.
Kwiat’s lab specializes in quantum information. Although his and Hosten’s experiment can be understood in terms of the equations devised in the 19th century by Augustin-Jean Fresnel and James Clerk Maxwell, the Illinois researchers chose instead to analyze their experiment in the quantum framework of spin–orbit coupling.
A quantum treatment could help identify quantum applications, Kwiat says. Moreover, to amplify the tiny separation enough to see it, he and Hosten exploited an esoteric quantum technique called weak measurement.
Theory first
That light could exhibit a spin Hall effect emerged from theoretical attempts to account for an effect predicted in 1955 by Fedor Fedorov 2 and measured in 1972 by Christian Imbert 3 : When a beam of circularly polarized light undergoes total internal reflection, the beam shifts transverse to the direction of propagation.
In 2004 Masaru Onoda of Japan’s National Institute of Advanced Industrial Science and Technology in Tsukuba and Shuichi Murakami and Naoto Nagaosa of Tokyo University saw in the Imbert–Fedorov effect a resemblance to the spin Hall effect, which Murakami and Nagaosa both study.
To emphasize the resemblance, Onoda, Murakami, and Nagaosa analyzed the case of photon wavepackets propagating in a photonic crystal whose refractive index varies periodically. 4 They predicted that the circularly polarized components of a linearly polarized beam would separate from each other by a distance of about 100 times the crystal’s lattice constant.
In principle, that separation, being several times larger than the wavelength of light, could be measured, but the experiment itself is hard to do.
Later in 2004 Konstantin Bliokh of the Institute of Radio Astronomy in Kharkov, Ukraine, and his father Yuri Bliokh of the Technion–Israel Institute of Technology in Haifa calculated the more easily realized case of a linearly polarized beam impinging on an air-glass interface. 5 Depicted in figure 1, that was the case Hosten and Kwiat investigated.
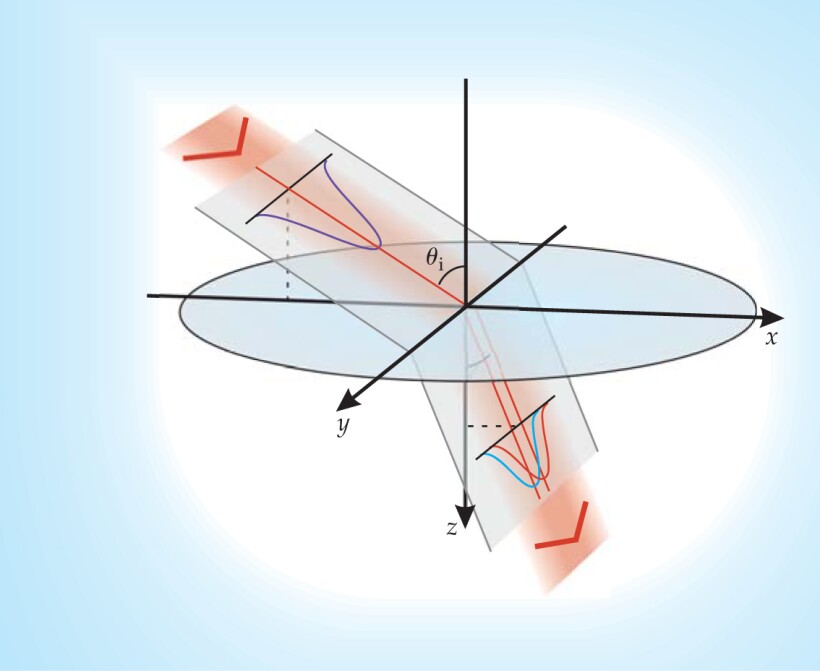
Figure 1. Spin Hall effect in light arises when a linearly polarized beam (purple) refracts at a boundary. Interaction between its polarization or spin degree of freedom and its geometric or orbital degree of freedom causes its right-hand (red) and left-hand (blue) circularly polarized components to separate.
(Adapted from ref. 1.)
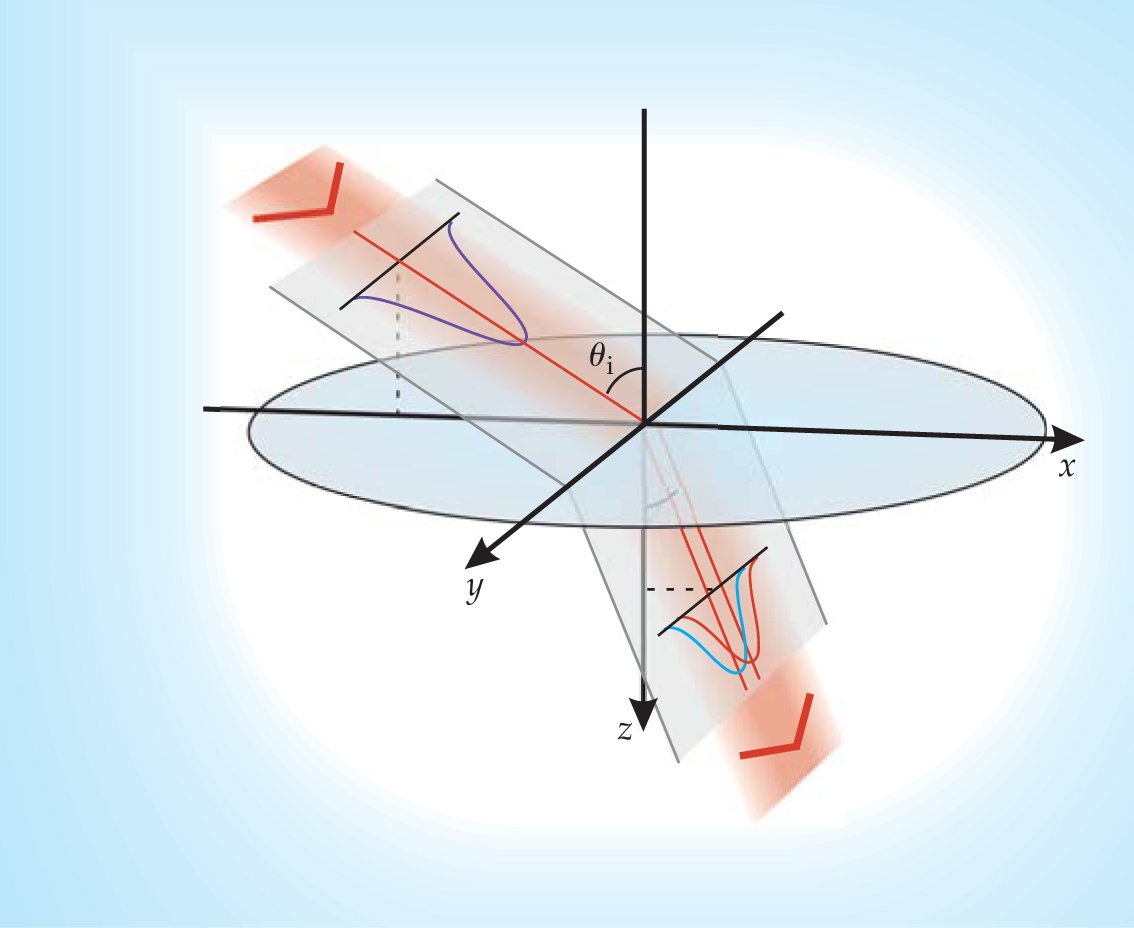
Although not strictly accurate, the easiest way to grasp how light exhibits a spin Hall effect is to look at figure 1 and consider one of the circularly polarized components—the right-hand one, say. In units of ℏ, the RH component has a spin angular momentum of +1 along the propagation direction. Before it strikes the glass, the linearly polarized beam comprises equal RH and LH components. Because of symmetry, the RH component’s total angular momentum about the normal, J z , must be conserved. After entering the glass, the RH component’s direction moves closer to the normal, increasing its spin angular momentum about that axis. To conserve J z , the RH component acquires an offsetting amount of orbital angular momentum by moving away from the normal in a direction perpendicular to the propagation direction (+y in the figure). The LH component, whose spin angular momentum is −1, also moves away from normal, but in the opposite direction. (For more on light’s orbital angular momentum, see the article by Miles Padgett, Johannes Courtial, and Les Allen, Physics Today, May 2004, page 35
Described in such terms, light’s spin Hall effect may seem far removed from its electronic cousins. The relationship becomes clearer when you look at the two equivalent ways of analyzing Hosten and Kwiat’s experiment.
A beam of light comprises an infinity of plane waves, each with a slightly different wave vector. When a beam meets an inhomogeneous medium, it refracts and changes direction. To keep the beam’s transverse nature, each of the constituent plane waves acquires different, circular polarization-dependent phases. Interference between the infinite set of plane waves yields a circular polarization-dependent lateral shift of the refracted beam.
Mathematically, the interference of the polarization and geometric phases looks just like the spin–orbit coupling that underlies the electronic spin Hall effect. Onoda, Murakami, and Nagaosa used that quantum approach in their 2004 paper. Hosten and Kwiat adapted it to account for their experiment and found it exactly equivalent to the classical approach taken by the Bliokhs.
Weak measurements
In Hosten and Kwiat’s experiment, the RH and LH components move apart by a tiny amount: no more than 70 nm at near-grazing incidence. Measuring such a small value is a formidable challenge. Jitter in the laser’s pointing direction, wobbles in the optical table, and currents in the intervening air all introduce micron-scale blur. Even if they didn’t, position-sensitive detectors have a precision of the same micron-scale order.
To meet the measurement challenge, the Illinois researchers adapted a technique called weak measurement, which was proposed 20 years ago by Yakir Aharonov, David Albert, and Lev Vaidman. 6 The three theorists considered the case of a Stern–Gerlach experiment whose beams and magnets are too weak to segregate up and down spins. Ordinarily, such a setup would yield not the two well-separated spots of Otto Stern and Walther Gerlach’s famous experiment but a peanut-shaped blob.
That unhappy situation would change, the three theorists argued, if you used two polarizing filters placed before and after the magnets. Orienting the filters’ axes at 90° would cut off all transmission, of course. But setting them just off perpendicular would have a surprising effect: The wavefunctions of those few atoms that made it through would interfere and boost the spin-dependent displacement by orders of magnitude.
Weak measurement does not provide a free lunch, however. In graphical terms, it pushes a peaked signal further away from the origin, making its displacement easier to determine. But the technique also reduces the peak’s amplitude, making it harder to see anything at all. If an experiment’s resolution is limited only by the statistics of photon counting, the two effects cancel. That was far from the case for Hosten and Kwiat’s experiment, in which systematic errors, not a paucity of photons, limited resolution.
Figure 2 shows the setup. To compare theory with experiment, Hosten and Kwiat took measurements at a range of incident angle θ i. If they’d used an ordinary, fixed-shape prism, changing θ i would also have changed the angle at which the beam left the prism’s back face. For all but one value of θ i, the light would therefore have refracted a second time and contributed a second, potentially confusing spin Hall separation.
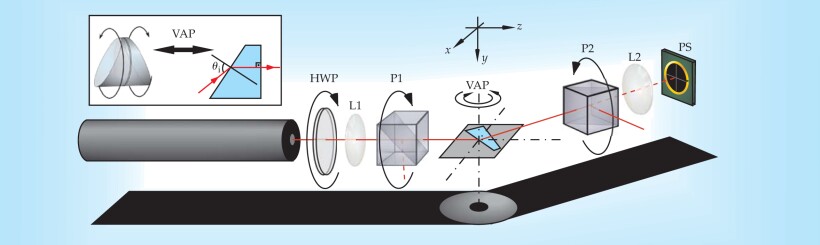
Figure 2. To induce light’s spin Hall effect, Onur Hosten and Paul Kwiat sent laser light through a linear polarizer P1, variable-angle prism VAP, and a second, nearly crossed linear polarizer P2. The VAP (insert) ensured that light left the prism normally regardless of incident angle θ i. The lens L1 caused the beam to diverge and, as a result, boosted the signal. The second lens L2 recollimated the beam, thereby helping to remove stray light. The position-sensitive detector PS measured the spin Hall effect by recording the shift of the beam in the y direction. Rotating the halfwave plate HWP offset the dependence on θ i of the refracted intensity, thereby ensuring that the detector received constant and optimal illumination.
(Adapted from ref. 1.)
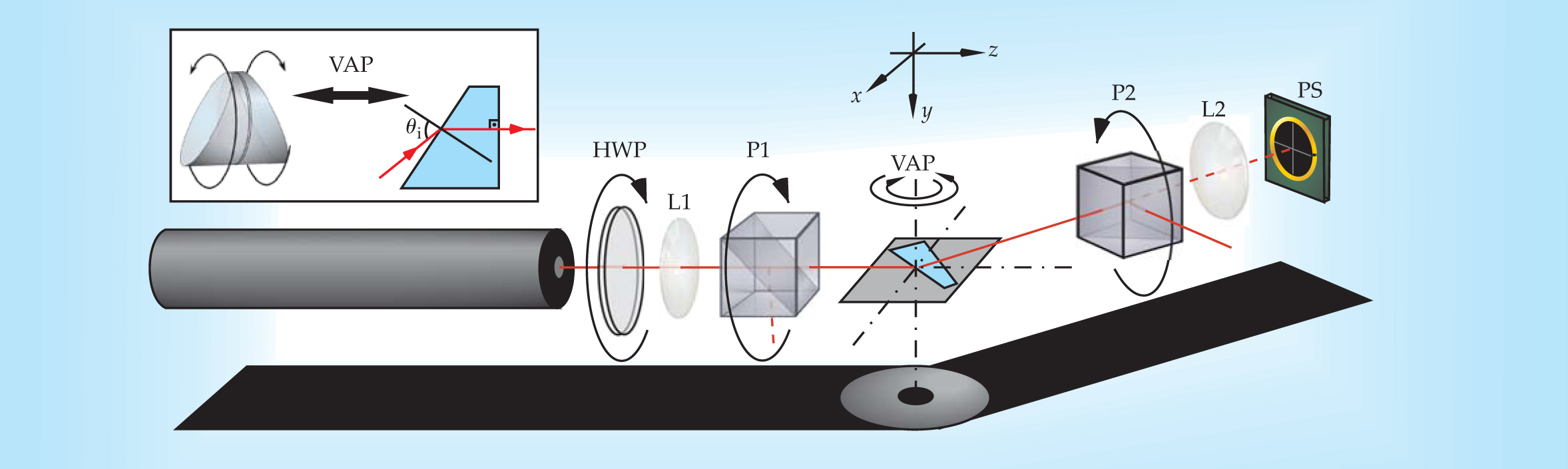
Hosten and Kwiat avoided that complication by using a variable-angle prism. By rotating the VAP’s two halves, they could ensure that the beam always left the prism’s back face normally—that is, without refracting and without causing a spin Hall effect.
The linear polarizer P1 set the angle γi, which the light’s polarization axis made with prism’s normal. Whatever the value of γi, the second polarizer P2 was oriented just off perpendicular to set up the condition for weak measurement.
By themselves, the three central components—P1, VAP, and P2—could amplify the spin Hall separation, but not by enough to yield a significant measurement. That’s where the lens L1 came in. It focused the beam onto a spot in the prism (the exact location doesn’t matter). When the beam emerged from the prism, the RH and LH components that were split by the spin Hall effect diverged.
In effect, the lens Fourier-transformed position (separation) into momentum (direction). The upshot was a boost in the separation by a factor of 104 and a resolution of 1 Å.
Hosten and Kwiat measured the separation for 21 values of θ i for 10 values of γi. The match to theory was almost perfect.
Past and future
The first to perform a weak measurement were Randall Hulet of Rice University in Houston and his collaborators Nicholas Ritchie and Greg Story. 7 In 1991 they achieved an enhancement factor of 30 when they measured the displacement of a beam’s horizontal and vertical polarized components in a birefringent crystal.
The Rice experiment served as a proof of principle. In 2004 Nicolas Gisin of the University of Geneva in Switzerland and his collaborators demonstrated that weak measurements could be used to determine useful properties of optical fibers, such as group velocity. 8
Gisin and Kwiat are currently investigating how to exploit the coupling that lies at the heart of the spin Hall effect for quantum information. A photon’s polarization and orbital angular momentum could each form an entangleable qubit. Meanwhile, as if to underline the generality of the spin Hall effect, condensed-matter physicists are also trying to exploit spin Hall systems for quantum information.
References
1. O. Hosten, P. Kwiat, Science 319, 787 (2008). https://doi.org/10.1126/science.1152697
2. F. I. Fedorov, Dokl. Akad. Nauk SSSR 105, 465 (1955).
3. C. Imbert, Phys. Rev. D 5, 787 (1972). https://doi.org/10.1103/PhysRevD.5.787
4. M. Onoda, S. Murakami, N. Nagaosa, Phys. Rev. Lett. 93, 083901 (2004). https://doi.org/10.1103/PhysRevLett.93.083901
5. K. Y. Bliokh, Y. P. Bliokh, Phys. Rev. Lett. 96, 073903 (2006). https://doi.org/10.1103/PhysRevLett.96.073903
6. Y. Aharonov, D. Z. Albert, L. Vaidman, Phys. Rev. Lett. 60, 1351 (1988). https://doi.org/10.1103/PhysRevLett.60.1351
7. N. W. M. Ritchie, J. G. Story, R. G. Hulet, Phys. Rev. Lett. 66, 1107 (1991). https://doi.org/10.1103/PhysRevLett.66.1107
8. N. Brunner, V. Scarani, M. Wegmüller, M. Legre´, N. Gisin, Phys. Rev. Lett. 93, 203902 (2004). https://doi.org/10.1103/PhysRevLett.93.203902




