Fermionic Atoms Appear to Pair Up Much as Electrons Do in a Superconductor

Researchers demonstrated quite dramatically nearly 10 years ago that bosonic atoms (those with integer spin) can collapse into a common ground state, known as a Bose–Einstein condensate (BEC), in which all the atoms march in lock step. This strange state is reached when the gas is so cold that the separate atomic wavefunctions overlap. It was natural, then, to look for the equivalent of BEC in a gas of fermionic atoms (with half-integer spin). Of course, the Pauli exclusion principle prevents even two fermions from occupying the same ground state, but there are ways around this quantum restriction.

One way is to combine fermionic atoms into bosonic molecules and then cool such molecules into a condensate. In fact, it has proved easier to create a BEC from molecules made of fermions than from molecules made of bosons, because the former have longer lifetimes. (See Physics Today, October 2003, page 18 .) Three groups reported last fall that they had formed fermionic condensates from such molecules at temperatures of a few hundreds of nanokelvins or less. One experimental team was from JILA, the University of Colorado at Boulder, and NIST in Boulder; ¹ a second was from the University of Innsbruck; ² and a third from MIT. ³

A second way to make a condensate starting with fermionic atoms is to form weakly interacting pairs of fermions, rather than tightly bound atoms in a molecule. The weakly interacting pairs, acting collectively, can collapse into a coherent many-body state. Witness the condensation of electron pairs in a Bardeen-Cooper-Schrieffer (BCS) superconductor or of pairs of liquid helium-3 atoms in a superfluid. Several groups are now racing to form such superfluids in ultracold atomic gases. Cindy Regal, Markus Greiner, and Deborah Jin of JILA, NIST, and the University of Colorado, have just reported evidence for this type of pairing—in a regime where the interatomic interactions are very strong, not weak. ⁴

Although BCS-type superfluids have long been studied in condensed matter systems, the atomic versions might offer new ways to control experimental conditions and could lend new insights in regions where fermions are strongly interacting. As the interactions grow in strength, many-body physics comes into play.

Dancing partners

The two types of pairing can be compared to the dancing styles illustrated in figure 1. Dimer molecules are like waltzing couples, while BCS pairs are akin to rock-and-rollers, who jive far apart. These two types of condensate behavior represent two extremes along a continuum. Molecules lie at one end, where a certain parameter a, which determines the sign and strength of the interaction, is small and positive; BCS-type pairs exist at the other end, where a is small and negative.

Experimenters can change the value of a by varying the magnetic field. For certain values of the field, a is small and positive; for others, it is small and negative. Between the two extremes lies the Feshbach resonance, at which the energy of pairs of scattering atoms approaches the energy of bound-state molecules. Near resonance, |a| goes to infinity, and the interactions grow very strong. Sweeping the magnetic field can take a gas through the crossover region, from the side where one expects a molecular BEC far from resonance, to the other side, where a BCS-type superfluid should exist, also far from resonance.

In the crossover region, theorists expect the only length scale to be the interparticle spacing. Thus, as one approaches the resonance from the BEC side, one expects the molecules to grow larger relative to the interatomic spacing. By the same token, approaching the resonance from the BCS side should cause the pairs to grow smaller. That’s why it’s so challenging to understand what’s going on in this intriguing but still mysterious region of strong interactions.

In search of pairs

A number of experimental groups have been looking near the Feshbach resonance for signs of coherent pairs and their superfluid behavior. One problem is how to detect the pairs. In most experiments on gases of ultracold atoms or molecules, researchers determine the outcome by expanding the gas and measuring the final momenta of the constituent particles. This tactic is not expected to work for pairs of atoms because the pairs are not likely to remain bound during the expansion.

The Colorado team solved this problem by devising a procedure that essentially “projected” atoms pairwise onto molecules: That meant sweeping the magnetic field in a certain way, as sketched in the inset of figure 2. Regal, Greiner, and Jin started with their gas on the BCS side of resonance, lowered the magnetic field and held it at a particular value, B _h, to allow pairs to form. Then they rapidly swept the field to a point B _f far from resonance on the BEC side. By this procedure, the researchers maintain, atoms that formed pairs at B _h will find themselves bound into molecules at B _f.

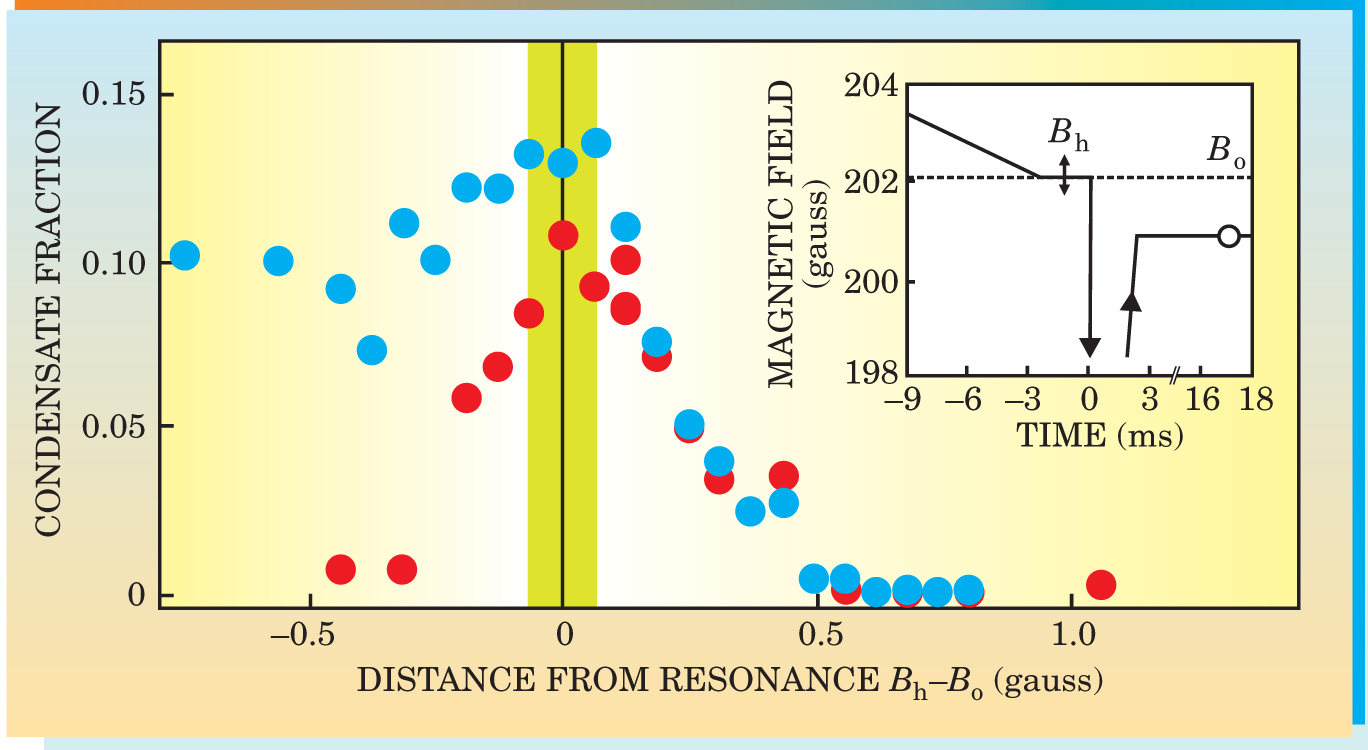
To determine the number of pairs in the original condensate, the Colorado team measured the fraction of molecules having zero momentum; that’s because the condensed pairs are expected to move about a fixed center of mass. The condensate fraction, measured as a function of position for three values of B _h, is shown in figure 3. Notice that the condensate fraction is sharply peaked when the field is close to the Feshbach resonance.

Regal, Markus, and Jin were not surprised to see a condensate peak develop when the magnetic field was held on the BEC side of the resonance because the three had already produced a molecular condensate there. ¹ But, as seen in figure 2, a condensate peak also grew at resonance and on the other side of it, where molecules cannot form. The researchers concluded that the condensate could not come from molecules but must stem from strongly interacting fermionic atoms, so they called it a fermionic condensate.

Jin is careful to point out that she and her colleagues do not see a condensate of weakly interacting pairs, such as the Cooper pairs of electrons in a superconductor. Such pairs can exist only far from resonance, a region that cannot be accessed by their technique.

In a comment submitted to Physical Review Letters, theorist Tin-Lun Ho of Ohio State University voiced his concerns about the experimental claims. Ho expects the size of the pairs formed at B _h to be much larger than the size of the molecules at B _f, and that difference would preclude any overlap. Furthermore, he points out, the collision rate in the strongly interacting regime should allow enough collisions during the magnetic-field sweep across this region that the momentum distribution in the molecular condensate will not be a faithful representation of that of the Fermi system. He remarks that the observed molecular condensate might, indeed, result from pairing condensation, but that other possibilities have not been adequately ruled out.

Jin answers that the sweep is adiabatic with respect to two-body physics, so that, for example, a large molecule can become a small molecule as the magnetic field is changed. The sweep is too fast, however, for changes in the many-body interactions, so such processes, she asserts, should not affect what she and her colleagues see.

Exploring new territory

Because the Colorado group formed a condensate in rather unexplored territory—the strongly interacting regime—other researchers are still digesting the results. Rudi Grimm of Innsbruck calls Jin’s paper a “very big step in the exploration of ultracold Fermi gases. It demonstrates the condensation of atom pairs in the strongly interacting crossover regime.” He cautions, however, that “this is a complicated many-body regime, where a distinction between molecules and atoms is not possible and no complete theoretical description is available.”

MIT’s Wolfgang Ketterle agrees that the Colorado group has produced an impressive paper and “gives us the first evidence for pair formation in the resonance region.” The experiment, he says, raises interesting questions about the distinction between preformed pairs of fermion atoms and molecules, especially in the crossover region.

Jin is excited about exploring fermion pairs in the strongly interacting region, which she feels is more interesting than the weakly interacting regime of low-temperature superconductors. A study of strongly interacting atom pairs might offer useful clues to the high-temperature superconductors: The interaction strength of atom pairs reported by the Colorado group translates to the coupling one would expect between electron pairs in a room-temperature superconductor.