Experiment and Theory Combine to Probe the Quantum Chemistry of Molecular Beams
DOI: 10.1063/1.1457251
Collisions make chemical reactions possible. Scattering collisions kick reactants into excited states; reactive collisions finish the job. Understanding these collisions—being able to predict and control them—is one of physical chemistry’s ultimate prizes. With it would come not just the satisfaction of explaining chemical reactions from quantum fundamentals, but also the ability to steer such industrially important reactions as combustion.
The quest is daunting. Molecules, even simple ones, possess a plethora of quantum states, whose interactions with each other and with those of approaching reactants can create a mixture of thousands of initial and final states. Faced with this quantum stew, physical chemists who study collisions reduce the number of complicating ingredients by working with molecular beams. In this approach, the number of states is pared down to a handful, offering the theorist the hope of predicting what’s going on.
Two recent papers have applied molecular beams to probe a simple system with unprecedented detail. Using crossed beams of nitric oxide molecules and argon atoms, a team led jointly by David Chandler of Sandia National Laboratory’s campus in Livermore, California, and Joseph Cline of the University of Nevada, Reno, has directly measured how NO molecules rotate after collisions. 1
Also using crossed NO and Ar beams, Hiroshi Kohguchi and Toshinori Suzuki of the Institute for Molecular Science in Okazaki, Japan, have explored collisions that either change or conserve NO’s electronic angular momentum. 2
By exploiting the latest experimental techniques and equipment, both teams stringently tested the latest theoretical calculations of the University of Maryland’s Millard Alexander, who joined Kohguchi and Suzuki on their paper. “Here we have the whole nine yards,” says Fleming Crim of the University of Wisconsin-Madison. “Elegant experiments along with high-caliber theory.”
Unpaired electron
The NO–Ar system is a popular choice for crossed-beam experiments for several reasons. Argon atoms, thanks to their symmetry and filled shells, lack internal modes of vibration or rotation and are chemically unreactive. The atoms’ ability to transfer and absorb only one form of energy—translational—simplifies the analysis of NO–Ar collisions.
Unlike its diatomic kin O2 and N2, NO has a single unpaired electron. Consequently, the transitions used to monitor the molecule fall conveniently in the spectral realm accessible with tabletop lasers.
The unpaired electron marks NO as a radical. Highly reactive, radicals act as go-betweens in thermal and photochemical reactions. They also trigger and propagate polymerization and combustion reactions. Chemists want to know more about how NO and other radicals behave.
But NO’s unpaired electron also makes the system difficult to model theoretically. One of the key ingredients in theoretical models is the potential energy surface (PES), a multidimensional entity that embodies the potential between the reactants at each configuration of their nuclei. In the case of NO-Ar, two slightly different, coexisting potential surfaces, dubbed A′ and A″, arise depending on whether the π orbital that harbors NO’s unpaired electron lies in the collision plane or points perpendicular to it. At large separations, the orientation of the electron doesn’t matter. But collisions take place on A′ and A″ simultaneously, with inevitable quantum complications.
Experiments don’t yield the PES directly. Rather, they measure various post-encounter properties, such as the reactants’ velocities, that can be related to the PES. One of the most fruitful diagnostics is the differential cross section (DCS), which gives the probability that a molecule will emerge from an encounter with a particular velocity, angular momentum, and quantum state.
Measuring the DCS, though, is a considerable challenge. Each differential in the DCS is a slice from the total scattering cross section. As with pizza, the more you slice, the smaller the portions. That’s good if you want to probe as many features of the PES as possible, but bad if you want each portion to contain a statistically significant amount of experimental data.
Imaging ions
To carry out their investigations, the Sandia–Nevada and Okazaki–Maryland teams used refined versions of the ion imager that was invented in 1987 by Chandler and Cornell University’s Paul Houston.
As in other molecular-beam experiments, the beams are created by first releasing pressurized gas into high vacuum. At the sudden drop of pressure, some of the molecules lose almost all their thermal energy and end up in their ground state. Collimating these cold molecules creates a narrow beam, whose speed is determined by the molecules’ mass.
Figure 1 shows the Okazaki lab’s apparatus and illustrates the basic geometry of both experiments. The two large silver-colored cylinders house the beams: one of pure Ar; the other, a beam of 5% NO and 95% Ar (a beam of pure NO would flow too slowly to get excited by an Ar beam). Both beams move at the characteristic Ar flow speed, which yields a collision energy of about 65 meV. That energy, if it’s completely converted into NO rotation, excites an NO molecule into the j = 16.5 total angular momentum state.

Figure 1. Crossed-beam ion imager at the Institute for Molecular Science in Okazaki, Japan. The large cylinders house the beams. The imaging equipment sits on top of the apparatus.
(Courtesy of Toshinori Suzuki.)

Because the NO molecules are randomly oriented, the Ar atoms hit them with a range of impact parameters, causing the NO molecules to fly off in a variety of directions with a variety of speeds and rotational states. The imaging equipment doesn’t detect these states simultaneously. Distinguishing them would be impossible. Instead, NO molecules in a particular quantum state are selectively ionized in a scheme known as REMPI (resonance-enhanced multiphoton ionization).
Illuminating the collision zone is a laser whose wavelength is selected to excite a particular postcollision quantum state. A second laser with a different frequency then ionizes the excited molecules, which, as ions, are accelerated by an electrode up toward a microchannel plate (MCP) above the collision zone. Because the ions each retain whatever transverse velocity they picked up from their collisions, they make their way to the MCP as an expanding cloud whose shape and size bear the imprint of the DCS. When an ion hits the detector, it creates a pulse of electrons that excites a sensitizer screen to make a spot of light. A charge-coupled device camera, located behind the MCP, records the location of the light spots until enough have accumulated to form an image.
The resulting ion image captures a two-dimensional projection of the expanding cloud of reactants. Mathematically transforming the image yields the DCS for a particular final quantum state. Other states are imaged by retuning the lasers’ frequencies.
The ion imager’s ability to capture all deflection angles continuously and simultaneously for a given state is what makes the device so powerful. Before its advent, a DCS had to be measured piecemeal by moving a nonimaging detector from position to position and combining the data.
State of the art
To see features in the state-resolved DCS requires a velocity resolution of a few percent. Achieving that resolution has depended on a series of improvements to Chandler and Houston’s original scheme.
In 1997, André Eppink and David Parker of the University of Nijmegen in the Netherlands replaced the simple mesh grid electrode in their ion imager with a set of electrostatic lenses. The lenses’ curved field focuses ions of the same velocity onto the same spot on the image, regardless of where in the interaction volume they lost their electrons. One of the largest sources of blurring is thereby mitigated.
To use as much of the camera’s field of view as possible, the ion imager in Okazaki incorporates a hexapole lens that makes sure that the expanding cloud of ions hits the camera dead center. Accurately modeling the beams and their interaction with the two lasers also helps to optimize the resolution.
With these improvements, the resolution of the images is mostly limited by the velocity spread of the beams. Reducing the spread—a tough problem—is under active investigation at Sandia, Okazaki, and other labs.
Sense of rotation
The Sandia–Nevada team sought to determine how NO molecules rotate after colliding with Ar atoms. By circularly polarizing their ionizing laser, the researchers could selectively image molecules rotating clockwise or counterclockwise.
What they found was fairly surprising. As figure 2 shows, the DCS has regions where the scattered molecules prefer to rotate either clockwise or counterclockwise. Furthermore, the regions’ features depend on how much total angular momentum j the NO molecules acquire after their collisions: the smaller the gain, the more complicated the pattern.

Figure 2. Collisions scatter nitric oxide molecules in different directions, depending on their sense of rotation and final angular momentum j. In these images, the collisions are viewed in their center of mass frame from above. The NO beam comes from the right; the Ar beam from the left. Because NO originated from the right, the left side of the images captures forward-scattered NO; the right side, back-scattered NO. The four images were produced by subtracting images of clockwise rotating molecules from those of counterclockwise rotating molecules. The color bar extends from purple (all clockwise) to red (all counterclockwise).
(Adapted from ref. 1.)
Accounting for this behavior proves how carefully even this apparently simple system has to be modeled. By combining Alexander’s PES model with classical dynamics, the Sandia–Nevada team could successfully reproduce its experimental results for high-j collisions, the main complication being the possibility that the rapidly rotating NO molecule could hit the Ar atom a second time before escaping.
But for low-j collisions, the classical approach fails. An NO molecule gains the most angular momentum when an Ar atom smacks it almost dead center. Lower-j collisions are subtler. Two different initial trajectories, feeling different areas of the PES, could converge with each other after a collision. Quantum interference ensues, and modeling the interactions requires treating the molecules and atoms as waves—which is what Alexander’s HIBRIDON suite of computer programs does.
The combination of HIBRIDON and the PES model could capture the overall features of the low-j collisions, but not all of them. Significantly, Alexander’s latest and best PES model, which takes a supercomputer one month to compute, did a better job of fitting the data than his previous version. Correctly predicting the rotational features in the DCS is clearly a sensitive test of PES models.
Change or conserve
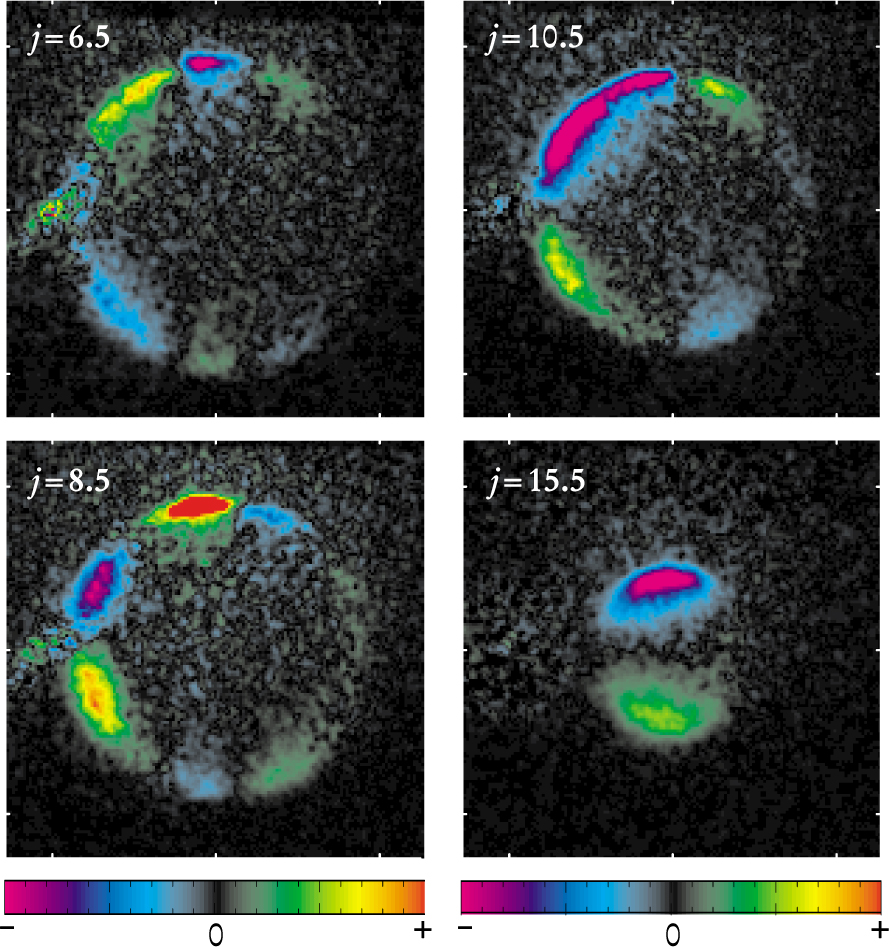
In their experiments, Kohguchi and Suzuki looked at two different types of inelastic collision: ones that either change or conserve NO’s total electronic angular momentum Ω.
In the ground state, the spin and orbital angular momentum of the unpaired electron point in opposite directions, so Ω =
Kohguchi and Suzuki measured the DCS for ΔΩ = 0 collisions at 11 different values of j and ΔΩ = 1 collisions at 9 different values of j.
The measured DCS varies considerably with final angular momentum state. But the experiments also show various features. At j = 7.5, for instance, the DCS has three peaks—at deflection angles of about 40°, 70°, and 110°.
As with the rotation data, predicting these and other features of the experimental data requires rigorous quantum mechanical treatment of the scattering. Alexander’s latest PES, coupled with HIBRIDON, can match Kohguchi and Suzuki’s data in most cases. But the combination doesn’t succeed completely. Discernable discrepancies occur for ΔΩ = 1 and the medium-sized j values of 5.5 to 8.5. The extreme sensitivity of the model to the difference between the A’ and A” surfaces could be the culprit.
Alexander sees evidence that varying the NO bond separation in his models might account for discrepancies. That suggestion is puzzling because exciting NO’s lowest vibrational state requires 233 meV—far more than the 64 meV available in the collisions Kohguchi and Suzuki measured.
Whether they play a role in low-energy scattering collisions or not, vibrations, and the complications they bring with them, must be incorporated into the next step in this enterprise: predicting the outcomes of collisions that transform their participants chemically.
References
1. K. T. Lorenz et al., Science 293, 2063 (2001).https://doi.org/10.1126/science.1062754
2. H. Kohguchi, T. Suzuki, M. H. Alexander, Science 294, 832 (2001).https://doi.org/10.1126/science.1063774




