Exotic spin textures show up in diverse materials
DOI: 10.1063/1.3120883
In its rest frame, an electron orbiting a nucleus feels a magnetic field proportional to its speed. The faster the electron orbits, the stronger the magnetic field, and the greater the coupling between the electron’s spin and orbital momenta.
Spin–orbit coupling is a hot topic because it offers a path to sort electrons by their spin, a necessary feature of spin-based electronics. But the path is not easy to find or follow. Despite its ubiquity, Spin–orbit coupling rarely shows up in an exploitable way. In many crystals, two symmetries, time-reversal and inversion, ensure that spin-up and spin-down electrons are degenerate.
Even when an applied field or a crystal’s structure breaks one of the symmetries, another obstacle blocks the path. Spin is not conserved inside a crystal. Although the net spin polarization averages to zero, it fluctuates randomly and locally as electrons make their way through the crystal.
There are ways around that obstacle. The trick is to find the right material and the right experimental conditions. Then, as three new papers demonstrate, Spin–orbit coupling begets remarkable phenomena.
Joseph Orenstein of the University of California, Berkeley, and his team have created a long-lived spin helix in a gallium arsenide quantum well. 1 Zahid Hasan of Princeton University and his team have observed a new form of matter, a topological insulator, in an alloy of bismuth and antimony. 2 Christian Pfleiderer of the Technical University of Munich in Germany and his team have discovered a structure akin to a vortex lattice in manganese silicide, a bulk ferromagnet. 3 All three phenomena manifest deep concepts also found in theoretical particle physics.
Persistent spin helix
Orenstein, who also works at Lawrence Berkeley National Laboratory, was interested at first in how long spin polarization survives before diffusing away. To that end, he and his team illuminated a semiconductor surface with an alternating pattern of left- and right-circularly polarized light. The light excited spin-polarized electrons to the conduction band, forming stripes of up and down spins.
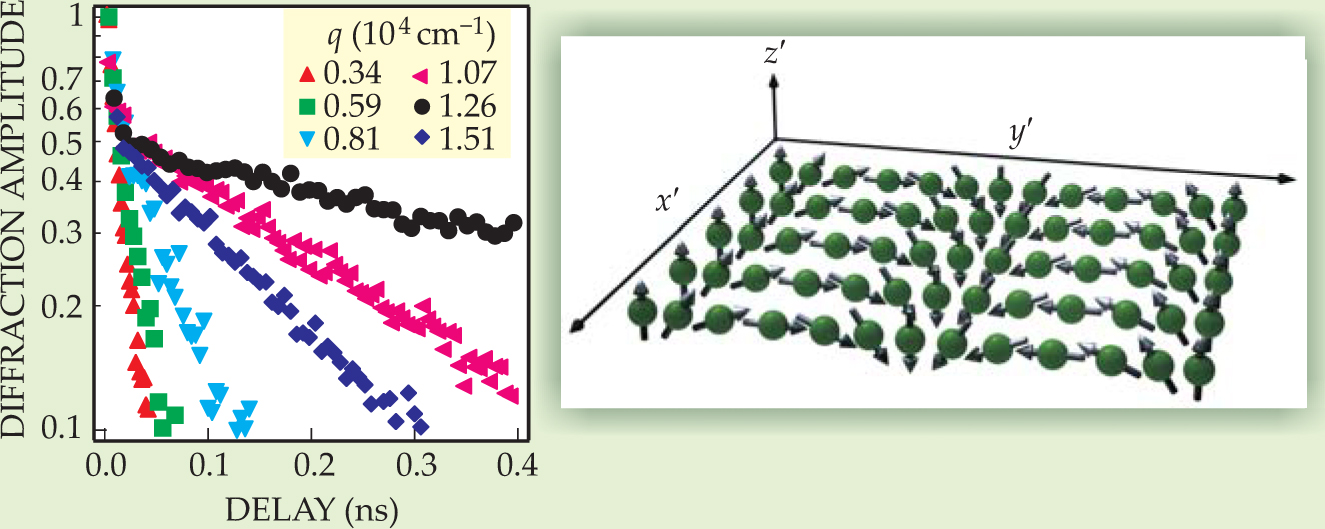
The stripey pattern served as a grating. When a linearly polarized probe beam was aimed at the surface, the resulting diffraction pattern embodied the spins’ polarization. Pulsing the excitation and probe beams and varying the delay between them yielded the polarization’s lifetime τ. The Berkeley researchers expected to determine how Spin–orbit coupling modifies τ. What they ended up discovering were two conditions that maximize τ.
The first condition is to use a quantum well in which two types of Spin–orbit coupling, Dresselhaus and Rashba, are contrived through doping to be equal. The second condition, worked out by Stanford University theorists Andrei Bernevig and Shoucheng Zhang, is to create a particular kind of coherent signal, a spin helix, and to send it through the quantum well with a particular wave vector.
Thanks to its shape and q dependence, the spin helix regains what Spin–orbit coupling usually removes: the SU (2) symmetry that conserves the polarization of isolated spins. In effect, Orenstein and his collaborators created an artificial instance of what Emmy Noether found in 1918: the fundamental association between symmetries and conservation laws.
Figure 1 shows one set of results. At 1 ns, the maximum lifetime is an order of magnitude longer than its unenhanced value, but it’s hardly infinite. A theoretical analysis by Victor Galitski and Tudor Stanescu of the University of Maryland accounts for the discrepancy, which arises from a cubic term in Dresselhaus coupling. Because the Maryland model fits the data so well, it implies, as Bernevig and Zhang predicted, that the spin helix is robust in the face of disorder.

Figure 1. A spin helix, depicted on the right, diffuses away when the pump pulse that generates it is turned off. The helix’s lifetime depends on its wave vector q and is determined by adjusting the delay between the pump pulse and a subsequent probe pulse that diffracts off the helix.
(Adapted from
Topological insulators
Six years ago, Hasan was trying to identify the origin of the unusually large thermoelectric effect in Bi-based alloys. His tool of choice, angle-resolved photo emission spectroscopy (ARPES), maps the band structure of electrons ejected from a sample’s surface.
Bismuth alloys, as Hasan found, have surface states quite different from those of the bulk. At first, he regarded the surface states as an annoyance. But after improving his setup to resolve surface states from bulk states, he came across predictions that the surface of Bi-based materials harbors a new state of matter, a topological insulator.
In a topological insulator, Spin–orbit coupling opens a gap in the otherwise gapless band structure, turning the bulk into an insulator and the surface into a metal whose two spin-dependent channels are topologically distinct. Remarkably, the surface states share the same Hamiltonian as the axion, an elementary particle invented in 1978 to resolve the puzzling absence of CP symmetry violation in quantum chromodynamics.
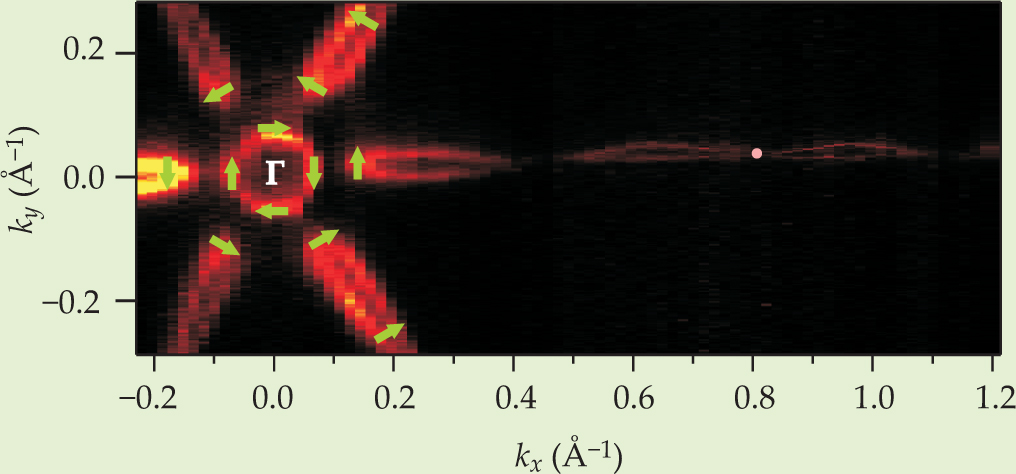
Adding Sb to Bi changes the shape and position of the two spin channels. When the proportion of Sb reaches 10%, one spin channel breaks into two pieces while the other remains intact. The corresponding Fermi surface develops pockets of paired spin channels—except at Γ, the origin of a crystal’s Brillouin zone.
The Γ point is where the topological insulator’s unusual nature becomes manifest and unambiguous. To search there, Hasan’s team added a component to its ARPES setup. Before reaching the detector, momentum-filtered electrons were accelerated through a gold foil, whose strong Spin–orbit coupling scatters electrons in a spin-dependent way. The electrons’ positions on the detector embodied not only the spin channel (up or down), but also the rotation the spins acquired as they moved in the channels.
Figure 2 shows one set of results. The spin structure around Γ clinched the case. Only one spin species, up, was present. If one of those electrons were to lap the circular region once, the direction of its spin would also make one complete rotation, not the two required to restore its original phase. Only a topological state has that nontrivial phase change, a Berry phase of π.
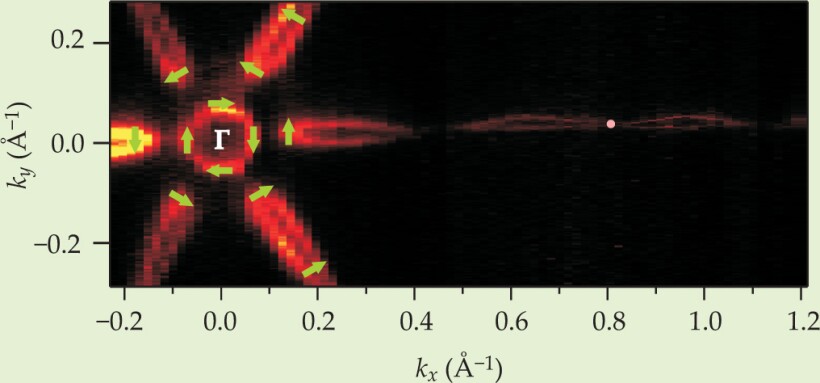
Figure 2. A topological insulator has metallic surface states whose band structure manifests a pocketed Fermi surface. Each pocket consists of nested pairs of spin-dependent channels, except at the Γ point, where only one channel is present. Princeton University’s Zahid Hasan and his collaborators not only mapped the Fermi surface, as shown here, but also determined the distribution of spin directions. The distribution around the Γ point (green arrows) verified the surface states’ topological nature.
(Adapted from
Skyrmion lattices
Unlike a GaAs quantum well or a BiSb surface, manganese silicide, the material in which Pfleiderer found his spin texture, is a bulk material. Its cubic structure breaks inversion symmetry and supports a kind of Spin–orbit coupling known as Dzyaloshinskii-Moriya.
The ferromagnetism of Mn atoms favors parallel spins, whereas DM coupling favors perpendicular spins. Together, the two tendencies yield a helical magnetic state that appears below 30 K at ambient pressure. Pfleiderer wasn’t interested in the helical state at first, but he thought studying it might help him understand another of MnSi’s states: a strongly interacting electron gas that appears under pressure.
During his investigation, Pfleiderer encountered an intriguing prediction made in 1989 by Alex Bogdanov and D. A. Yablonskii: Anisotropic magnetic materials might, with the application of an external magnetic field, be coaxed into forming a lattice of vortex-like structures. Mathematically, the vortices resemble skyrmions, the elementary particles that Tony Skyrme postulated in 1962 to account for the diversity of baryons. Unfortunately, in MnSi the skyrmion lattice was predicted to be unstable and hard to observe.
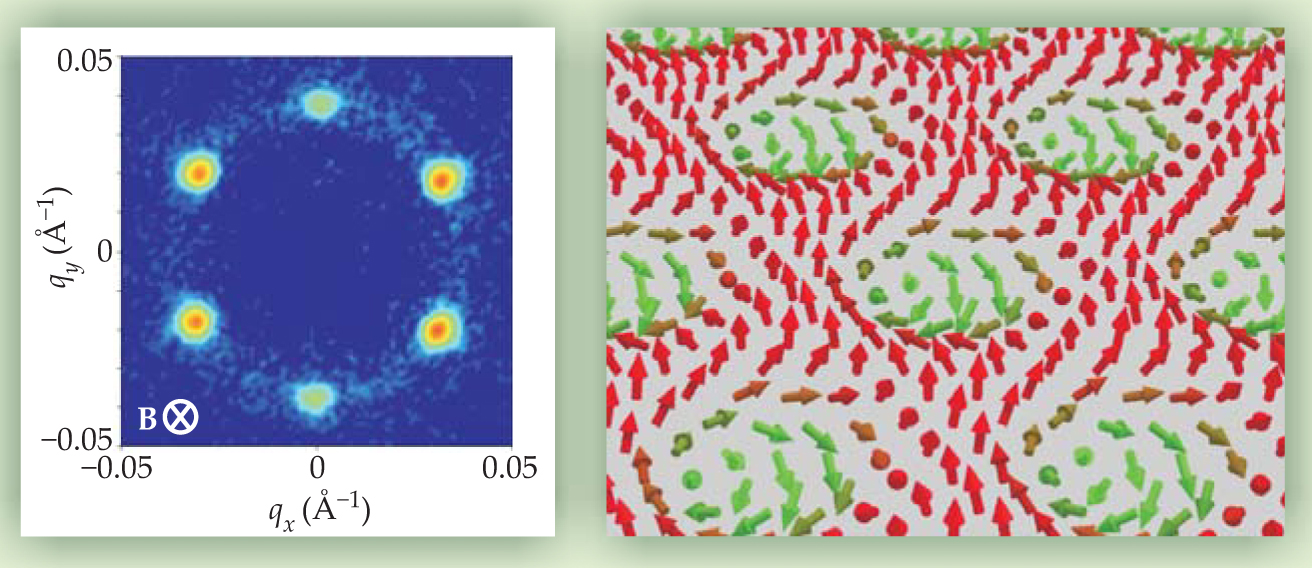
Meanwhile, Pfleiderer and his team began to investigate the potential of MnSi’s helical phase for processing information. Neutron diffraction was their tool, and a serendipitous mistake in orienting the sample in the beam and magnetic field led to a startling discovery. Instead of the four- or twofold symmetry they expected, they saw a hexagonal pattern of diffraction spots, implying threefold symmetry. Figure 3 shows one set of data. Remarkably, the pattern persisted when the sample’s orientation was changed with respect to the magnetic field and neutron beam. Whatever structure was causing the pattern was tied to the field, not to the crystal lattice.
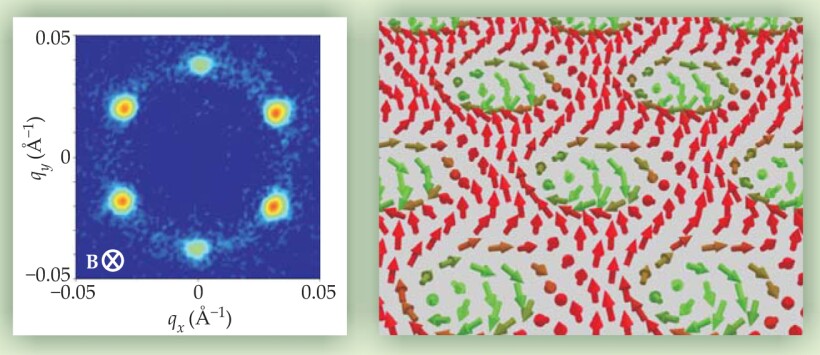
Figure 3. A skyrmion lattice reveals itself in a neutron diffraction pattern as a set of six hexagonally distributed spots, as shown on the left. The underlying crystal lattice, being cubic, can’t yield such a pattern. The configuration of spins in the skyrmion lattice is shown on the right. Each skyrmion’s axis extends into the sample and follows the direction of the applied magnetic field, even when the sample’s orientation in the field is changed.
(Adapted from
Pfleiderer’s theory colleagues, Achim Rosch and Benedikt Binz at the University of Cologne, came up with an explanation. Thermal fluctuations stabilize the skyrmion lattice, turning it into a proper ground state and making it far easier to form and observe than expected. Pfleiderer’s original goals of understanding MnSi’s strongly correlated state and exploiting its helical states for data storage now seem closer.
References
1. J. D. Koralek et al., Nature (in press).
2. D. Hsieh et al., Science 323, 919 (2009). https://doi.org/10.1126/science.1167733
3. S. Mühlbauer et al., Science 323, 915 (2009).




