Cooling molecules the optoelectric way

The electrons within an atom are the quintessential example of quantum mechanical objects. But the atoms themselves, being three or more orders of magnitude heavier, can usually be treated classically. However, when a gas of atoms is made cold enough, it enters a new regime in which quantum effects become important. Collisions, for example, must be described as the interaction of waves, not as the ricocheting of billiard balls. At colder temperatures still, the atoms’ Fermi or Bose statistics come into play. (See Physics Today, December 2001, page 14 .)

In an ultracold molecular gas, a richer array of quantum phenomena emerges. Molecules lack spherical symmetry, so in their collision dynamics, angles and orientations matter. And molecules can undergo a nearly limitless range of chemical reactions.

Bringing molecules into the ultracold regime has proved a challenge. The techniques researchers use to cool atoms don’t generally work on molecules, and so far, the only way to create an ultracold (roughly, submillikelvin) molecular gas is to assemble the molecules out of atoms that have already been cooled. (See the article by Debbie Jin and Jun Ye in Physics Today, May 2011, page 27 .) But the only molecules that have been created that way are weakly bound pairs of alkali metal atoms, potassium–rubidium, for example, that would be unstable at higher temperatures.

Gerhard Rempe and colleagues (Max Planck Institute of Quantum Optics, Garching, Germany) have now demonstrated a method with the potential to cool almost any molecule. ¹ They used it to cool a trapped gas of fluoromethane (CH₃F) from 390 mK to 29 mK, with the promise of still lower temperatures to come.

Cooling atoms

One of the main workhorses of ultracold atomic physics is laser Doppler cooling, in which a gas of atoms is bombarded with laser light slightly detuned from an atomic resonance so that the atoms preferentially absorb photons that oppose their momentum. By repeatedly absorbing and spontaneously emitting photons, the atoms gradually lose kinetic energy—that is, they are cooled. (See Physics Today, December 1997, page 17 .)

Each absorbed photon saps only a tiny amount of an atom’s kinetic energy, so the absorption–emission cycle must be repeated tens of thousands of times to cool a sample from 1 K to 1 mK. Each cycle must return the atom to the same quantum state (or one of a few, if multiple cooling lasers are used). That’s feasible for atoms, which have discrete electronic energy levels. But molecules have rotational and vibrational degrees of freedom that endow them with a multitude of long-lived, low-lying states into which they can decay, and thus hinder Doppler cooling.

David DeMille and colleagues at Yale University have achieved some success in Doppler cooling molecules. ² (See also Physics Today, January 2010, page 9 .) They’ve shown that they can cycle molecules through the same few quantum states without losing too many of them to the “wrong” states. But they have yet to cool molecules in a 3D trap, and their technique is limited to certain simple molecules.

Up and down the hill

Rempe and colleagues’ optoelectric technique capitalizes on the availability of many molecular quantum states. The basic scheme is shown in figure 1. In a gas of molecules confined to an electrostatic trap, the researchers focus on a few pairs of rotational states with very different electric dipole moments. Almost any molecule that lacks inversion symmetry has a permanent dipole moment, and each of its rotational states has a different average value of that dipole moment, so there are many possibilities to choose from.

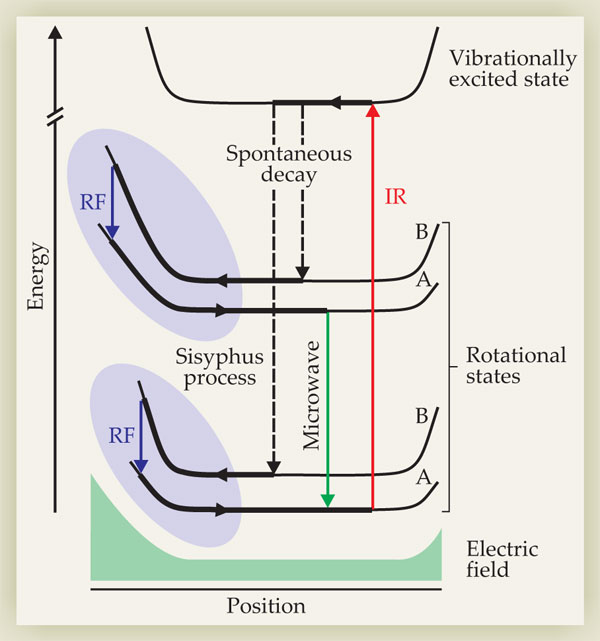
A molecule in one of the states marked “B” in figure 1 has a large dipole moment, so it interacts strongly with the inhomogeneous trapping field. As its thermal energy carries it toward the edge of the trap, it climbs a steep potential hill and loses kinetic energy. When it reaches the point where states A and B differ by an energy equal to an applied RF field, that field stimulates a transition between the two states, and the molecule, now in state A, rolls down a shallower hill back to the center of the trap. Molecules are pumped from the A states back into the B states via a series of transitions that include a vibrational spontaneous emission, which ensures that the cycle cannot go in reverse.

Because the kinetic energy lost in state B is greater than the kinetic energy gained in state A, the net result is cooling. The amount of cooling per cycle depends on how far the molecules are allowed to travel up the potential gradient before they come into resonance with the RF field. By starting with a high-frequency RF field and incrementally decreasing the frequency, one can in principle reach ultralow temperatures after only a few cycles.

That protocol—a type of Sisyphus cooling, so named because the molecules are forever climbing hills—was proposed in 1983 by David Pritchard for cooling atoms, using magnetic fields and magnetic dipole moments instead of electric ones. ³ But because other atom-cooling methods work so well, it never caught on.

Slow progress

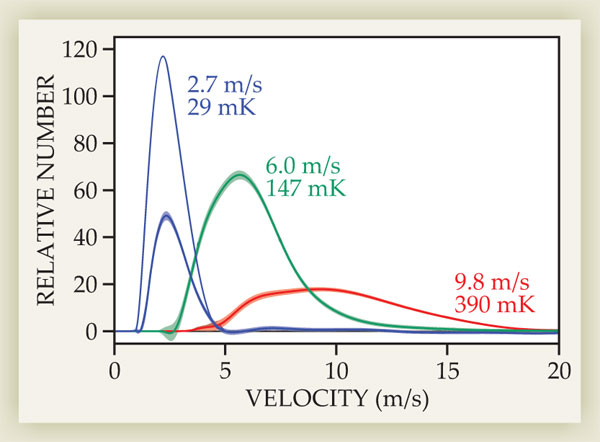
Rempe and company used several methods to check that they had actually cooled their sample. The most straightforward was to release the atoms from the trap and infer their velocity distribution from their time of flight to a detector. As seen in figure 2, that measurement shows that with a 1.22-GHz RF field, they cooled the sample from 390 mK to 147 mK. But when they incrementally decreased the RF field to 390 MHz, they achieved a final temperature of 29 mK.

Progress toward the quantum regime is marked not only by temperature but by phase-space density, the number of molecules per available quantum state. A quantum gas—a Fermi gas or Bose–Einstein condensate—is characterized by a phase-space density of order one. The gases of KRb molecules ⁴ created from ultracold K and Rb atoms have phase-space densities of about 0.1; the best directly cooled molecular gases until now, about 10⁻¹¹. Rempe and colleagues don’t report an absolute phase-space density, but they found that they increased their sample’s phase-space density by a factor of 29 (it could have been a factor of 70 if it weren’t for the atoms lost from the trap), so they’re still many orders of magnitude away from a molecular quantum gas.

What’s holding them back from achieving lower temperatures and higher phase-space densities is a limitation not of the cooling technique but of their experimental design. Optimizing the experiment is a slow process, because their detector—a quadrupole mass spectrometer—is four orders of magnitude less efficient than simple spectroscopic detection of atoms. That inefficiency could be mitigated by populating the trap with more molecules to begin with, but in the meantime, each measurement must be repeated many times to accumulate enough signal. (Because the detection efficiency is both low and unknown, the researchers don’t know exactly how many molecules are in their trap, a necessary ingredient for calculating the absolute phase-space density.)

For several reasons, the researchers chose CH₃F as their first molecule to cool. It has a large electric dipole moment, which makes it easy to trap. Its spontaneous decay from the vibrationally excited state is relatively fast. And it’s relatively easy to detect with the quadrupole mass spectrometer. But the cooling method should be applicable to almost any molecule with a permanent electric dipole moment. Formaldehyde (CH₂O) has a similarly large dipole moment and is of particular chemical interest. And on the horizon? “I’m dreaming of a Bose–Einstein condensate of water,” Rempe says.

Fast evaporation

Meanwhile, researchers at JILA, led by Ye, have demonstrated a molecular application of another cold-atom technique, evaporative cooling. ⁵ In principle, the technique is simple: From a collection of particles with a thermal distribution of energies, removing the most energetic particles decreases the average energy per remaining particle. As long as the particles can be rethermalized, the process can be repeated and the temperature lowered further.

The problem is, the elastic collisions that rethermalize the particles must compete with inelastic collsions—chemical reactions or conversions of rotational, vibrational, or electronic energy into translational energy—that remove particles from the sample. Molecules have generally been found to have poor elastic-to-inelastic ratios at the temperatures that have been achieved so far.

But Ye and colleagues made a fortuitous discovery while studying hydroxyl radicals at the relatively modest temperature of 50 mK. They never expected OH, a highly reactive species, to be a candidate for evaporative cooling. But as Ye recalls, once they had observed inelastic collisions, “We asked our theory collaborators to calculate the collision cross section, and they came back and told us that we should also look for elastic collisions because they predicted the elastic cross section to be larger than the inelastic one.”

Armed with that prediction, Ye and colleagues loaded their 50-mK OH radicals into a magnetic quadrupole trap. They found that, in just 70 ms, forced evaporation could cool the gas by at least an order of magnitude in temperature and three orders of magnitude in phase-space density. Although the result so far is limited to OH, the researchers raise the questions of whether other similarly promising candidates have been overlooked, or whether a cold gas of OH could be used to cool a gas of another molecule.