Carefully timed radio pulses sustain quantum phase

To build a quantum computer, you need to pull off a delicate balancing act. Whatever objects embody the qubits must preserve their quantum coherence—which requires isolation. But the qubits must also be stored, initialized, entangled, manipulated, and read out—which requires violating their isolation and spawns errors.

Schemes have been devised to correct those errors (see the article by John Preskill, Physics Today, June 1999, page 24 ), but they entail deploying additional qubits beyond the ones needed for computation. Given the difficulty in scaling up from one qubit to many (the record is currently eight entangled qubits), the fewer qubits devoted to error correction, the better.

It would be even better if errors could be suppressed in the first place. Michael Biercuk, Hermann Uys, and John Bollinger of NIST in Boulder, Colorado, and their collaborators have just demonstrated a method for preserving qubit coherence. ¹ The NIST method is based on spin echo, a venerable technique borrowed from nuclear magnetic resonance (NMR), and is implemented on trapped ions, one of the leading qubit contenders.

A key feature of the method is its generality. Trapped ions, quantum dots, Josephson junctions, and other embryonic technologies for quantum computation have different sources of decoherence; the spectra of their respective environmental noise are different. In principle, the NIST method works for any noise spectrum—even an unknown one.

Dynamical decoupling

The idea of using radio pulses to forestall decoherence originated in the 1950s with Erwin Hahn. The resonant signal from a collection of nuclear spins will weaken as the spins, each in a slightly different magnetic environment, precess at different rates and fall out of phase with each other. Hahn realized that administering a single short radio pulse of the right frequency and duration—a spin-echo pulse—will send the spins back to their original state and restore coherence.

Two pairs of NMR pioneers—Herman Carr and Edward Purcell, Saul Meiboom and David Gill—devised a way to string together Hahn’s spin-echo pulses to sustain coherence. Their sequence, known now as CPMG, works well in NMR contexts, where noise spectra fall off steeply with frequency. In quantum information contexts, noise spectra may be different and the sensitivity to decoherence is higher. Would CPMG work there too?

Götz Uhrig, a theorist at the University of Dortmund in Germany, tackled the question in 2007 by considering a two-level system in a bath of bosons. ² His model mimics an electron spin qubit in a quantum dot and yields a noise spectrum dominated by high frequencies—the opposite of the NMR case.

The pulses in the CPMG sequence are equally spaced. In his calculations, Uhrig allowed the pulse intervals to vary. To his surprise, small adjustments to the intervals boosted the sequence’s ability to suppress errors by orders of magnitude. Last year, Benjamin Lee, Wayne Witzel, and Sankar Das Sarma of the University of Maryland conjectured that Uhrig’s dynamical decoupling sequence, now dubbed UDD, worked for generic noise spectra. ³ That same year, Wen Yang and Renbao Liu of the Chinese University of Hong Kong proved the conjecture. ⁴

Penning-trapped beryllium

Applying UDD to sustain qubit coherence requires precise control of pulse timing. It also requires qubits that respond reliably and predictably to the pulses. When Biercuk and Uys joined NIST’s ion storage group last year, they found a suitable testbed for UDD: beryllium ions held in a Penning trap.

Penning traps are cylindrical. Axial confinement comes from a static electric field; radial confinement, in circular orbits, comes from a static magnetic field and the resulting Lorentz force. At millikelvin temperatures, Coulomb repulsion settles a cloud of Penning-trapped ions into a rotating crystalline array. By adjusting additional rotating electric fields, the cloud’s aspect ratio can be controlled. Figure 1 shows the pancake-like cloud the NIST team used.

The rotation makes the ions difficult to address individually, but such access isn’t needed to test dynamical decoupling. Global addressing and read-out suffice. If, as was the case in the NIST experiment, the ions don’t perturb each other, a single measurement of all the ions is effectively the same as a measurement of a single ion, but with a higher signal-to-noise ratio.

The magnetic field needed for radial confinement Zeeman-splits the ions’ valence states into spin-up and spin-down levels; it’s also strong enough to pull the splitting into the microwave band. The NlST experiments used 124 GHz. That frequency is low enough that there’s little likelihood of provoking a spontaneous emission, as would be the case in the IR or optical.

The experiment begins when about 1000 ⁹Be⁺ ions are loaded into the trap and cooled. Optical and microwave pulses initialize the ions in a superposition of spin-up and spin-down states. The spin-up state fluoresces, whereas the spin-down state is dark. Each experimental run ends with a pulse that will put the ions in the spin-down state—provided they’ve retained their coherence. For each pulse sequence, measuring fluorescence at fixed times after the final pulse therefore determines how much decoherence-induced error has accumulated.

Without any coherence-sustaining pulses, quantum information embodied by the relative phase between an ion’s spin-up and spin-down states would decay within a few milliseconds. How well CPMG, UDD, or any other sequence forestalls decoherence depends on the noise spectrum.

If the trapped ⁹Be⁺ ions were part of a real quantum computer, their performance-limiting noise would come primarily from magnetic-field fluctuations, which shift the Zeeman transition. In the NIST experiment, the decoherence-inducing effect of a fluctuating magnetic field, or indeed any environmental source of noise, can be mimicked by modulating the microwave control system. When no modulation is applied, S(ω) ∝ ω^-4, and UDD provides no advantage over CPMG. But as Figure 2 shows, UDD outperforms CPMG when S(ω) ∝ ω, confirming Uhrig’s original idea.

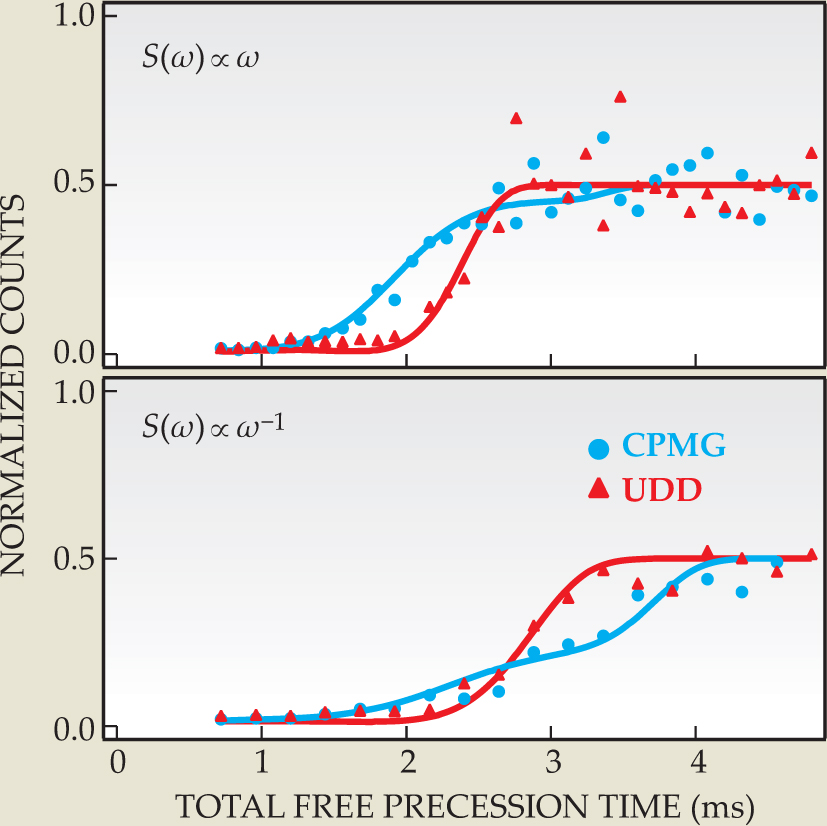
The plots in Figure 2 are for sequences of six pulses. The NIST researchers found they could subject their ions to 1000 pulses, which boosted the coherence time to 200 ms. They also developed a feedback system to accommodate arbitrary and unknown noise spectra. By monitoring decoherence, the feedback system adjusts the timing between the pulses until it finds the set of intervals that minimizes the accumulation of error.

Trapped ions are hardly the only contender for realizing a quantum computation. Proving that dynamical decoupling works for any kind of noise spectrum is not much good if the pulses can’t be applied with the requisite accuracy to, say, Josephson junctions or quantum dots, and if the corresponding qubits don’t respond with the requisite fidelity. Those and other qubit technologies need further experimental advances if they’re to benefit from dynamical decoupling.

Another concern is whether the pulse sequences can be incorporated into more general qubit operations. The ions trapped and manipulated in the NIST experiment behave like a quantum memory. Preserving coherence while performing CNOT and other logical operations is more complicated. Further theoretical and experimental work will determine whether dynamical decoupling is generally applicable to all the tasks of a hoped-for quantum computer.