Anyons abound in 1D quantum gases

Figure 1.

For all the oddities that Edwin Abbott invited his readers to imagine in his classic novella Flatland—that women are straight lines, men are polygons, and rain falls from the north—most aspects of physics and chemistry in the fictitious world of two spatial dimensions are the same as in our universe of three. Flatland contains, among other things, trees, gunpowder, food, water, and solid materials: all things that seemingly require the same atoms and molecules that exist in 3D.

Abbott was writing in the 1880s, so he would have had no way to anticipate how dimensionality could affect the nature of matter. It wasn’t until the 1920s, with the development of quantum theory, that it started to become clear how much of our everyday world depends on the fact that electrons are spin-½ fermions, no two of which can occupy the same quantum state. That restriction gives rise to atomic shell structure, the periodic table, all of chemistry as we know it, and the fact that matter takes up space.

And only in the 1970s did theorists start to realize that the situation might be different in different numbers of dimensions. ¹ In 3D, particles must be either integer-spin bosons or half-integer-spin fermions, but 2D and 1D worlds have no such requirement. Their particles can be anyons—a term coined by Frank Wilczek ² in 1982—with any spin. If subatomic particles in Flatland (or in its 1D counterpart Lineland) had anything other than exactly half-integer spin, there’d be no Pauli exclusion principle, and atoms would look completely different.

Flatland analogies often come up in discussions of the physics of reduced-dimensional systems such as graphene, the one-atom-thick form of carbon (see the article by Andrey Geim and Allan MacDonald, Physics Today, August 2007, page 35 ). But for the most part, just like in Abbott’s story, the inhabitants of those systems are the same fermions and bosons as in 3D. The full spectrum of 2D and 1D peculiarities has remained largely untapped.

But that situation is changing. Two groups—one led by Hanns-Christoph Nägerl ³ at the University of Innsbruck in Austria, the other by Markus Greiner ⁴ at Harvard University—have now coaxed atoms in 1D quantum gases into behaving like anyons. The experimental implementations differ, but one feature they have in common is that the researchers can tune their particles along the full continuum from fermions to bosons.

Flatland phases

It’s a seemingly simple—but deceptively subtle—argument that underlies the rule that particles in 3D must be either fermions or bosons. When two identical particles are exchanged, as in figure 1, the system’s wavefunction picks up a phase that depends on the particles’ spin: For bosons, the phase is 0, and the wavefunction is unchanged; for fermions, the phase is π, and the wavefunction is multiplied by −1.

Other values of spin would correspond to other phase angles θ that have the effect of multiplying the wavefunction by the complex number e^iθ. But, the argument goes, exchanging two particles twice is the same as not exchanging them at all, so applying the phase twice must return the wavefunction to its original value. Because 1 and −1 are the only square roots of 1, fermions and bosons are seemingly the only options.

And in three or more spatial dimensions, that’s true. In 2D, however, there are two topologically distinct ways to exchange the particles—by rotating them clockwise or counterclockwise—that can’t be smoothly transformed into one another. Two clockwise swaps aren’t the same as no swaps, so they needn’t return the wavefunction to its original value.

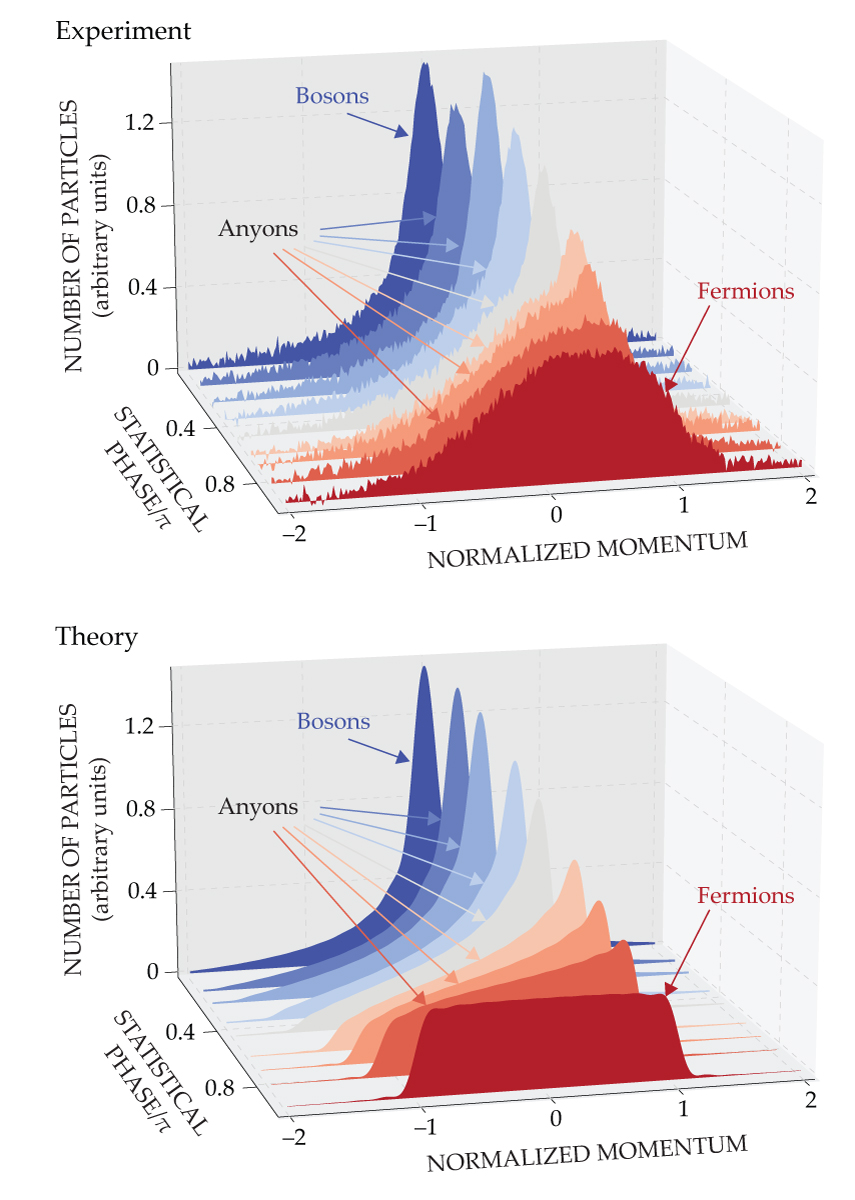
Figure 2.

So anyons can exist in 2D—and, in fact, they do. In the fractional quantum Hall effect, a phenomenon that emerges at low temperatures and under strong magnetic fields, fractionally charged quasiparticles form out of a 2D layer of electrons. Theory held that the quasiparticles would also have a fractional phase θ, but that prediction was extremely difficult to experimentally confirm. In a solid-state system, there’s no easy way to grab two quasiparticles, manually swap their places, and measure the phase change that results. So although the fractional quantum Hall effect was discovered in the 1980s (see Physics Today, December 1998, page 17 ), it was only in 2020 that experiments showed that the quasiparticles were indeed anyons. ⁵

When the number of spatial dimensions is reduced from two to one, the intuitive picture becomes harder to grasp. The distinction between clockwise and counterclockwise exchanges no longer exists—and neither, for that matter, does the distinction between exchanging the particles and not exchanging them. Particles in 1D can’t change places without passing through each other. And because the particles are identical, as soon as they occupy the same space, there’s no way to tell whether they really swapped places or merely bounced off each other and returned to their original positions.

Nevertheless, 1D anyons can exist, as both Nägerl’s and Greiner’s groups demonstrated through variations on a common theme: Bosons tend to pile up in the same quantum state, whereas fermions spread out into different states. Anyons act in an in-between way—neither bunching nor antibunching—and although the specific nature of that intermediate behavior can be hard to intuit, theorists can predict it.

Quantum gases of ultracold trapped atoms, used by both groups, have proved to be a useful platform for studying many-body phenomena. Atoms in a trap exhibit many of the same behaviors as electrons in a solid, but they can be manipulated and probed in ways that electrons cannot.

Nägerl and colleagues created their anyons by exploiting a phenomenon called spin–charge separation. ⁶ With a few dozen identical bosonic atoms in a 1D trap, a traveling excitation in the system’s spin degrees of freedom creates a phase of −θ in the spin part of the wavefunction. The charge portion of the wavefunction (really the atomic positions, because the atoms play the role of electrons in a solid) therefore needs to compensate with a phase of θ, which defines the statistical behavior of all the atoms.

The more the spin wave is accelerated, the larger the value of θ becomes, so the researchers can tune it to any value from 0 to π or beyond. They probe the anyonic correlations by abruptly turning off the trap and releasing the atoms. The atoms fly apart with the momentum they had at the moment of their release.

The researchers’ momentum measurements are shown in figure 2. As expected from theory, the particles show boson-like bunching into a single momentum state at θ = 0 and fermionic antibunching at θ = π. (In the latter case, the experimental data aren’t as nicely antibunched as theory predicts, because the experiment averages over many implementations of the system, each with a slightly different range of possible momenta.) Other values of θ yield intermediate—anyonic—momentum distributions.

Figure 3.

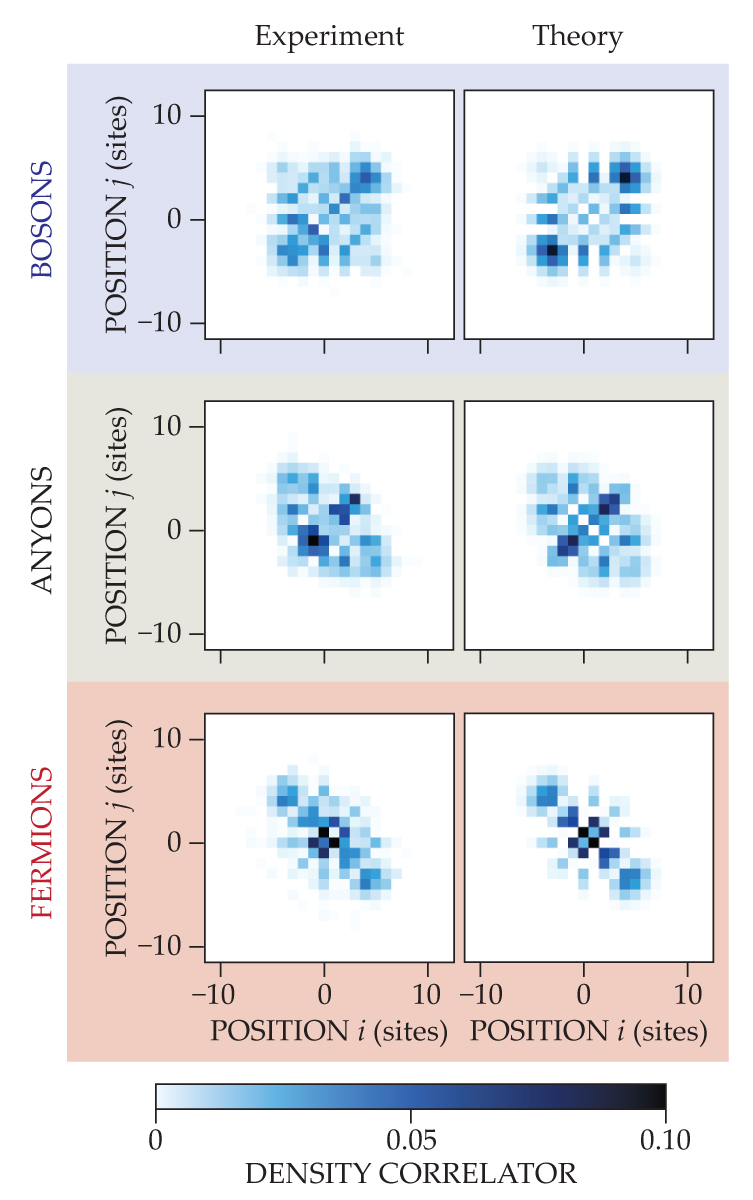
Whereas Nägerl’s group created gases of 30-some anyons, Greiner and colleagues have so far focused on studying just 2. Rather than a continuous 1D trap, they looked at a 1D lattice of discrete sites, into which they loaded two identical bosonic atoms. By driving the system with lasers, they engineered a scenario in which the atoms hopped freely among the sites, and whenever the atoms occupied the same site, the wavefunction picked up a phase: θ if one atom passed the other from left to right, and −θ if from right to left.

Rather than measuring the momenta, Greiner and colleagues observed fractional exchange statistics by tracking the lattice sites i and j that their atoms occupied, as shown in figure 3. For θ = 0, the atoms showed a bosonic preference to occupy the same site, with an enhanced density along the i = j diagonal. For θ = π, they showed a fermionic tendency to be farther apart, with density along the i = −j antidiagonal. Anyons, once again, showed an intermediate behavior.

What for?

The 2D anyons that show up in the fractional quantum Hall effect have tantalizing potential uses in topological quantum computing. Because the system retains information about how many times the anyons have encircled one another, it can be used as a quantum memory. And because the wavefunction phase shifts depend only on the number of particle exchanges, they’re insensitive to small changes in the anyons’ trajectories, and the memory is robust against noise.

The 1D quantum-gas anyons lack that possible application. But from a fundamental physics perspective, they have the considerable advantage of continuous tunability of the phase θ. (Quantum Hall anyons, in contrast, arise from a discrete set of fractional quantum Hall states that must be prepared one at a time.) So, for example, the researchers could explore the possibility that θ might act as an order parameter that drives a phase transition. Such a transition, if it exists, would be an inherently reduced-dimensional phenomenon; it wouldn’t be even conceptually possible in our 3D world, where particles are limited to the binary options of fermions and bosons.

Both groups are also interested in studying interactions between pairs and groups of anyons. Greiner and colleagues have already observed the bizarre and unexpected phenomenon of anyon bound states that travel in only one direction. If they can elucidate the binding mechanism, they could get a step closer toward understanding what atoms and molecules would actually look like in Flatland.

This article was originally published online on 25 July 2025.