Ants know the secret to avoiding traffic jams

Groups of interacting agents in a confined system, whether cars on a highway or insects in a tunnel, often generate clogs that can persist for long durations. For tasks that demand a steady flow of agents, with each performing a repetitive task, those clogs hinder the collective goal. When a traffic jam happens, it’s not just detrimental to each driver; rather, the total number of cars traversing the road at any given time is reduced. Road engineers put a lot of thought into infrastructure design to keep traffic flowing as smoothly as possible. Insects have instinctive strategies for accomplishing the same goal.

With GPS and mobile communications technology, humans can see other cars on the roads and make informed decisions about avoiding congested areas or venturing out in the first place. But for agents operating in other confined systems, like ants working in a nest or micromachines carrying drugs in a patient’s blood, it’s impossible for an individual to know about the other participants and the conditions affecting the overall system.

Fire ants (Solenopsis invicta), like most ants, work together to dig complex tunnel networks. Now Daniel Goldman and colleagues at Georgia Tech have found that workers follow counterintuitive and seemingly counterproductive rules to optimally excavate the collective’s early-stage tunnels. ¹ The team used tools from soft-matter physics ² to analyze how clusters formed and dissolved in a collection of ants.

When the ants go marching in

For his research, Goldman sought an organism that met a behavioral study’s basic requirement of repeating a task over and over again. He settled on fire ants. “If the organism is local and easy to collect with a shovel and bucket, that’s even better,” he said. Fire ants arrived via infested shipping crates in the US 80 years ago and now thrive in the subtropical southeastern states.

To learn about ants’ soil excavation, Goldman built a model environment whose transparent enclosure contained 0.25-mm-diameter glass particles mixed with water to mimic the damp soil that ants typically remove. The model ensured that moisture conditions stayed the same in each experiment. Goldman’s earlier work showed that a fire ant contributed to digging complex nests by entering a tunnel, collecting a load of soil that was always the same size, and climbing back out. In the early stages of nest construction, ants built vertical tunnels one body length in diameter. The narrow tunnels helped the climbing ants as they transported the glass particles: Close proximity to walls allowed the ants to recover from slips. But although the tunnel structure helped individual ants do their jobs, it slowed excavation when high-traffic conditions led to clogging. ³

Goldman, his postdoc Daria Monaenkova, and PhD student Bahnisikha Dutta wanted to understand how each ant learned to mitigate clog formation in the absence of information about others’ activity. That required tracking each ant’s visits to each tunnel. To tell the 30 fire ants apart, the researchers painted the ants’ abdomens with unique color patterns, as shown in figure 1. They filmed the ants digging tunnels in a 25-cm-wide soil-like pack, recorded the total length of the tunnel over time, and cataloged the location of each worker seen on camera.

Figure 1.

Although individual ants entered and exited the tunnels hundreds of times, only three to five ants in a tunnel were found to carry glass particles at any given time. Other ants idled outside. Ants that encountered even a small traffic jam on their way to the tunnel retreated without collecting any particles. The team proposed that the seemingly energy-wasting behavior served as a feedback mechanism that reduced the severity of clogs and sometimes even prevented them from forming.

The researchers’ analysis of the data revealed that 30% of the ants did 70% of the work. To test whether the labor distribution could be attributed to the efforts of a handful of superants, the researchers removed the five best-performing ants. Even in the absence of the hardest workers, the remaining ants achieved the same total work output as before.

Taking time off work

Goldman and coworkers then turned to traffic-flow models as a guide to devising simulations and theories of ants excavating tunnels. Traffic engineers use a model known as a cellular automaton to simulate the movement of vehicles on a highway. ⁴ In such simulations, a collection of cells on a grid evolves through discrete time steps and follows a set of rules based on the states of adjacent cells. For traffic engineers, those cells represent vehicles; for Goldman and company, ants. Too many vehicles create a traffic jam, whereas too few do not generate significant flow. Fewer cars on the road is not a bad outcome for traffic, but having too few ants limits the work that can be done. An intermediate, critical number of vehicles maximizes traffic flow for cars and, similarly, work output for ants.

Ants offered a novel twist to traffic-flow simulations. Not only did each simulated ant have to reach the end of the tunnel, but it also had to return to the entrance. In the simulations, a “tunnel” with a width of two cells was occupied by soil, empty space, or ascending or descending ants. The ants could move, change directions, excavate, deposit a soil particle, or rest. A hard-working ant had a high probability of entering the tunnel, whereas a lazy ant had a low probability. If an ant in the tunnel found its path toward the excavation area blocked, it reversed direction and headed back toward the entrance. As in the live-ant experiments, activity was measured by counting instances when ants visited the tunnel.

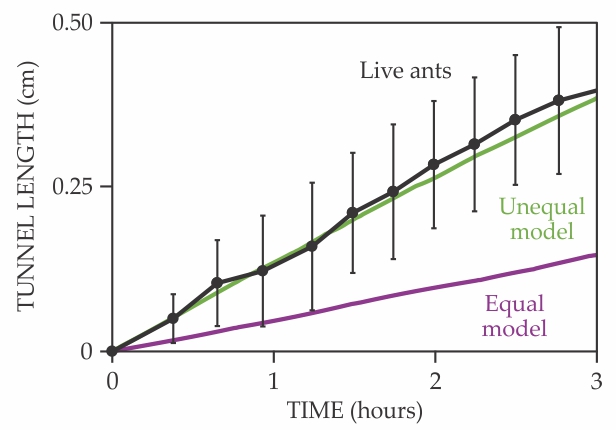
Goldman’s student William Savoie demonstrated that the simulated ants moved at maximum efficiency, without jamming, when following an optimized division of labor similar to that observed in the biological experiments. Simulated ants that used an equal division of labor increased tunnel occupancy with an increasing number of ants, and thus exhibited optimal flow for only a few population sizes. The excavated tunnel lengths over time for experiments and simulations are shown in figure 2. Goldman’s collaborators Meredith Betterton and Hui-Shun Kuan at the University of Colorado Boulder developed a simple theoretical model to rationalize the schemes; it essentially demonstrated that on average the ants maintained a density of one ant in a tunnel at a time during the optimal division of labor.

Figure 2.

Repeating the simulations with different tunnel widths revealed that wider tunnels led to decreased performance. Goldman’s team hypothesized that narrow tunnels not only made it easier for ants to climb and gather particles but also allowed them to expend less energy than they would digging wider tunnels. “Narrow tunnels are a feature of the system, not a bug. There’s only one way to optimize the work flow,” says Goldman.

Serving the collective

The biological studies and computer simulations captured group behavior. To test ant strategies in a confined experimental situation with complex, unpredictable interactions, Goldman’s student Vadim Linevich built robots designed to excavate a three-robot-wide channel filled with magnet-containing plastic spheres, shown in figure 3. Each oval-shaped robot wheeled into the channel, scooped up a ball or cluster of balls, and carried the load back to the entrance.

Figure 3.

The robots followed simple instructions triggered by onboard sensing of the surrounding environment. Push switches attached to their outer shells let the robots detect collisions. The switches triggered strategies such as steering away from a jam and adjusting their course to lessen clog formation.

Linevich and Goldman first examined how excavation performance, defined as the number of plastic balls deposited at the tunnel entrance per minute, changed as the number of robots increased. They found that going up to three robots increased efficiency, but adding a fourth caused a jam and halted productivity. Team member Jeffrey Aguilar applied measurement techniques from soft-matter and glass physics to calculate the robots’ spatial overlap while clogs formed and dissolved. He found that the robotic ants’ orientation determined whether a small cluster had time to dissolve before another ant came along. If not, a fourth ant would create a jam that spanned the tunnel width. That cascading scenario is reminiscent of how particles in soft-particle systems slow to a glassy state as density increases. ⁵

Linevich then programmed the robots with two protocols that revealed different mechanisms for mitigating clogs. In the first, the robots reversed direction if they had not successfully reached the excavation site within a given time. That protocol limited the duration of clogs. In the second, some robots dug eagerly and others dawdled. That protocol reduced the occurrence of clogs. Both protocols reduced the glass-like clog formation associated with four eager robots. Even then, the relatively clumsy robots couldn’t match the ants’ performance. Still, the robots offer an experimental system for testing how individual behavior affects traffic flow in confined situations.

The findings help to explain how individual agents in a confined active system can perform tasks when they lack knowledge about the system’s overall structure and the positions of their fellow agents beyond their nearest neighbors. The results could help scientists develop robot swarms that perform tasks in confined spaces, such as carrying drugs through the bloodstream or searching through disaster rubble.