Acoustics Experiment Shows Why It’s So Hard to Make Out the Heroine’s Words at the Opera

A frustrated listener might well define grand opera as musical theater where you have a hard time making out the words even when they’re being sung in your own language. Conceding the point, many opera houses nowadays always flash surtitles above the proscenium. Comprehension is particularly difficult in the higher reaches of the soprano register. Hector Berlioz long ago warned composers not to put crucial words in the soprano’s mouth at high notes.

A recent study at the University of New South Wales in Sydney, Australia, lays most of the blame on an inescapable tradeoff dictated by the physical acoustics of vowel differentiation and singing very high notes. Acoustical physicists John Smith and Joe Wolfe, working with physics undergraduate Elodie Joliveau, have carried out an experiment that demonstrates why different vowel sounds are almost impossible to distinguish when sopranos are singing in the highest octave of their range. ¹

The experimental subjects were eight professional operatic sopranos. Joliveau is herself a soprano, Wolfe is a composer and woodwind player, and Smith plays the double bass. The experimenters used equipment developed by Smith and Wolfe for the analysis of acoustic resonances in musical instruments and in the vocal tract during ordinary speech. The equipment is, in fact, designed to help adults master the sounds, especially the vowels, of a new language. It’s also being applied to the correction of speech pathologies.

Vocal tract resonances

In ordinary speech or singing, the fundamental pitch frequency f ₀ is determined by the tension applied to the vocal cords. (The alternative term “vocal folds” is more anatomically precise.) The output at f ₀ is accompanied by a harmonic series of overtones nf ₀. If there were no resonant effects in the vocal tract, which extends from the cords to the lips, the amplitudes of successive harmonics would fall off by about 12 decibels per octave. But the vocal tract does present a sequence of resonant frequencies R_i . Consequently, any harmonic nf ₀ from the vocal cords that happens to lie close to one of the R_i is enhanced.

To make the various vowel sounds, a speaker or singer must change these vocal-tract resonances by altering the configuration of tongue, jaw, and lips. The distinction between different vowel sounds in Western languages is determined almost entirely by R ₁ and R ₂, the two lowest resonances. That is, vowels are created by the first few broad peaks on the amplitude envelope imposed on the overtone spectrum by vocal-tract resonances.

For the vowel sound in “hood,” as pronounced by a male speaker of “standard” Australian, R ₁ ≈ 400 Hz and R ₂ ≈ 1000 Hz. By contrast, to produce the vowel in “had,” he must raise R ₁ and R ₂ to about 600 and 1400 Hz, respectively, by opening his mouth wider and pulling the tongue back.

For women, the characteristic resonance frequencies for a given vowel sound are roughly 10% higher. But for both sexes, the pitch frequency f ₀ in speech and singing is generally well below R ₁ for any ordinary vowel sound—except when sopranos are singing really high notes. And that’s when vowel distinctions become problematic.

Striving to be heard in the last row of a large opera house, often in competition with a full orchestra, a soprano needs all the help her vocal-tract resonances can provide. But R ₁ is useless as an amplifier when f ₀ exceeds it. The highest octave of the soprano range typically extends from C5 (523 Hz) to C6 (1047 Hz). That octave also happens to be the beginning of the frequency range in which human hearing is most sensitive.

In the 1970s, Johan Sundberg (Royal Institute of Technology, Stockholm), a pioneer in the analysis of singing acoustics, presented evidence that the tricks sopranos are traditionally taught for maintaining volume at high notes (“open your mouth very wide and smile”) actually serve to raise R ₁ toward f ₀. But, with the technology then at his disposal, Sundberg could not confirm his conjecture directly. ² For any one note, the singer’s frequency spectrum could sample the resonant structure of the vocal tract only at f ₀ and its overtones—that is, at discrete frequencies hundreds of hertz apart.

The Sydney experiment

By contrast, the Sydney group’s new technique probes the vocal tract almost continuously over the frequency range 0.2–4.5 kHz. Adjacent to a microphone touching the subject singer’s lower lip is an acoustical current source—the output horn of an electronic sound synthesizer that is calibrated to present the microphone with a flat broadband frequency spectrum when the singer is silent with her mouth closed.

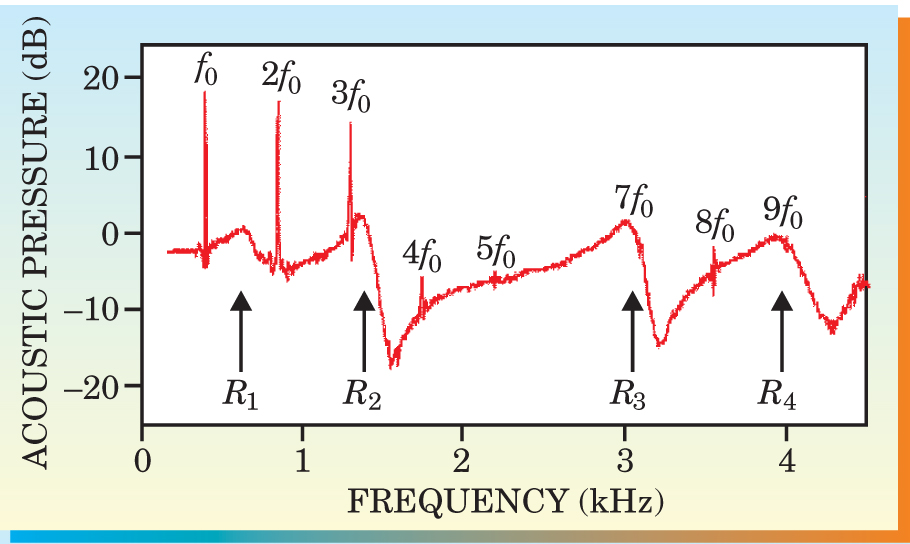
In the Sydney experiment, the subject sang a sustained note with a given vowel sound while the synthesizer was on. Thus the frequency spectrum recorded by the microphone (see figure 1) combined the narrow spikes of the singer’s fundamental pitch frequency and its overtones with the much broader, but still well-defined, peaks that exhibit the modification of the synthesizer output by the resonances in that particular vocal-tract configuration. The spectrum in figure 1 was produced by a soprano sustaining the note A4 (440 Hz) for four seconds with the vowel sound in “hard.” The observed R ₁ in that case, about 650 Hz, was comfortably above the 440-Hz fundamental. And it was essentially the same as the R ₁ for that vowel sound in ordinary speech.

But what happens to the first vocal-tract resonance as the soprano goes up the scale to higher notes? Figure 2 plots the Sydney experiment’s measured change of R ₁ with increasing f ₀ for four different vowel sounds. At low pitch frequency, the R ₁ values are well separated and roughly independent of f ₀. They are about the same as they are in speech.

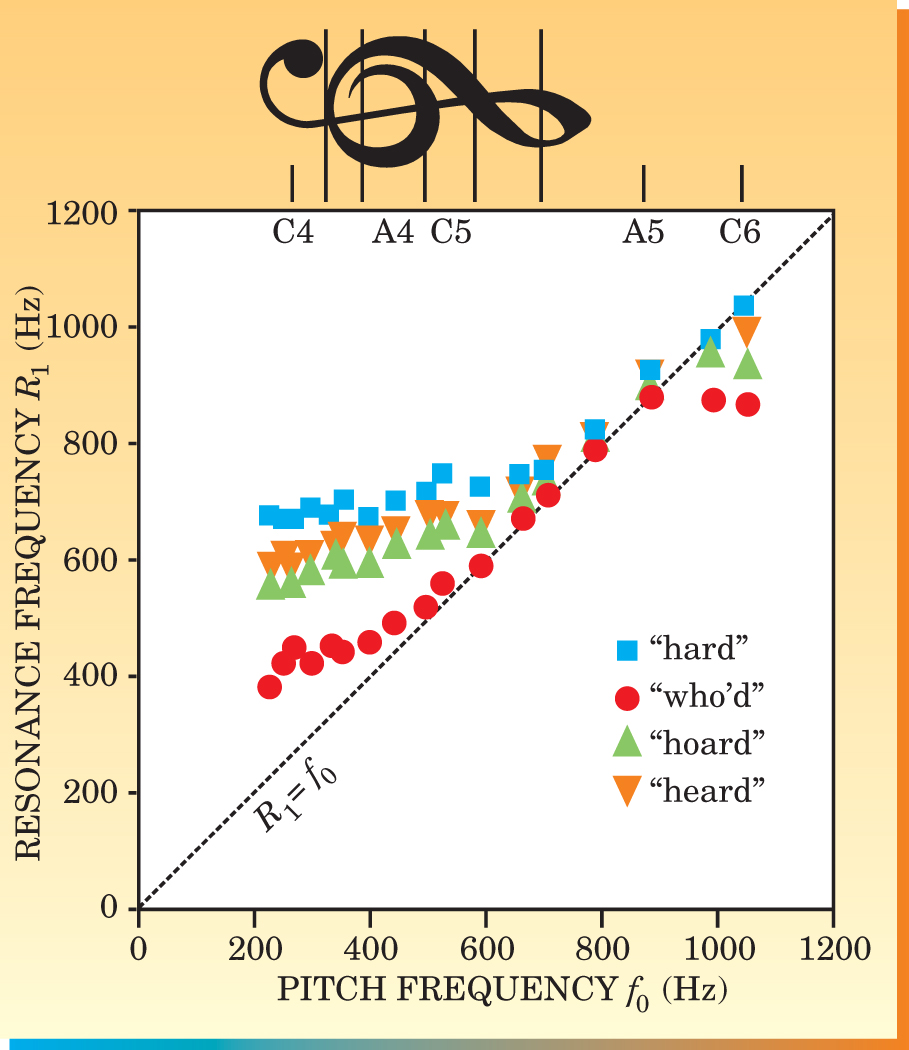
If these plateaus were to continue to higher pitch frequencies, f ₀ would eventually surpass R ₁ and thus render the first, and most important, resonance acoustically useless. But as f ₀ approaches the diagonal that delineates f ₀ = R ₁ we see that R ₁ begins to rise, as Sundberg had argued, eventually becoming equal to f ₀ and thus strongly amplifying the fundamental note produced by the vocal cords. This “tuning” of R ₁ also serves the important function of minimizing unintended variation of loudness and timber with pitch.

Morphologically, what’s happening is that the trained singer is progressively flaring the front end of her vocal tract by lowering her jaw and pulling back the corners of her mouth in an exaggerated smile (see figure 3). The first resonance of an unflared cylinder is at the frequency for which the cylinder’s length is $\frac{1}{4}$ of the wavelength of a standing acoustic wave. The effective length of an adult’s vocal tract is typically 15–20 cm. But just as in brass instruments, the greater the flaring for a given total length, the higher is R ₁.

Understanding the words

The asymptotic convergence of f ₀ and R ₁ in figure 2 continues all the way up to C6, except for the vowel sounds in “hoard” and especially in “who’d.” Wolfe explains: “For those vowels you round your lips, and in that facial mode it’s uncomfortable, if not anatomically impossible, to raise R ₁ above a kilohertz.” Composers tend to avoid such vowel sounds at the highest notes. A notable exception was Beethoven, who became notoriously indifferent to singers’ limitations after he went deaf. In the choral movement of his ninth symphony, the soprano soloist has to sing her highest note (B5 = 989 Hz) on the umlauted U in flügel (wing), an even more daunting vowel sound than that in “who’d.”

As the first vocal-tract resonances converge with increasing f ₀, it becomes more and more difficult to distinguish words. If the plot depends crucially on whether the heroine is singing “bird,” “barred,” or “bored” at A5 (880 Hz), you’d better keep your eyes on the surtitles rather than the dagger.

What if a soprano were willing to forgo the benefits of raising R ₁ for high notes? That would only partially solve the comprehensibility problem. Even for constant, well-separated R ₁ frequencies, vowel distinction becomes increasingly harder with rising pitch. That’s because f ₀ is the spacing between overtones. The higher the note, therefore, the more sparsely does the sound produced by the vocal cords sample the resonant spectrum of the larynx and mouth.

On the Sydney music-acoustics group’s Web site, ³ one can listen to the gradual disappearance of all vowel distinction as a soprano ascends the scale from C4 to C6. The site also poses a “soprano challenge.” Any classically trained soprano who believes she can maintain clear vowel distinctions at the top of the scale is invited to contact the group. “If we find someone who can indeed defy what we think is a fundamental physical limitation,” says Wolfe, “that would be the basis for a very interesting study.”