Features

Article

The rubidium atomic clock and basic research

NOV 01, 2007

The vapor-cell atomic clock finds application today in the global positioning system and telecommunications. To improve and miniaturize the humble device for future applications will require a deeper understanding of atomic and chemical physics.

DOI: 10.1063/1.2812121

James Camparo

You’re returning home from a conference, in a rental car on a dark, rainy road 50 miles from the airport; you’re running out of time to catch your flight, and you’re lost. As little as 10 years ago, this would have been the stuff of travel nightmares, to be shared with colleagues during a coffee break between conference sessions. Today it is less of a nightmare and more of an inconvenience. You pull your car to the side of the road, program your desired destination into the rental car’s navigation system, and let it calculate a direct route to the airport from your present location using signals from orbiting GPS (global positioning system) satellites. Thankfully, you make it home without an exciting but harrowing story to tell family and friends.

Unseen and forgotten in this now-routine use of GPS are the atomic clocks. The propagation times of signals traveling 20 000 km from space to Earth are measured at the nanosecond level, and from those measurements, positions are calculated to within, in some cases, a few centimeters. More generally, modern systems ranging from cell-phone communications to satellite navigation take advantage of atomic clocks, in particular the capabilities of small, low-power, rubidium vapor-cell clocks. How the vapor-cell clock came to play such an important role in modern timekeeping is a story that goes back half a century, and one that highlights the close interplay between basic science and technological innovation.

The vapor-cell atomic clock

The vapor-cell atomic clock is an unpretentious device. Light from a small discharge lamp passes through a vapor of rubidium atoms housed in a glass cell and is detected by a photodiode. The light intensity transmitted by the vapor is used to lock the frequency of an RF signal to an atomic transition. The RF signal can then be down-converted to generate a train of one-second pulses for timekeeping. Given its conceptual simplicity, the extent to which the vapor-cell clock’s realization relies on basic atomic and chemical physics is quite striking.

Since time intervals are defined as the elapsed phase of some stable oscillation, all clocks are, at heart, frequency standards. Just like in your wristwatch, the timekeeping signal in an atomic clock is derived from a quartz crystal oscillator. However, a crystal oscillator’s RF frequency ν _xtal depends on a number of environmental factors, such as humidity, vibration, and radiation, that can cause the clock to either speed up or slow down. In the vapor-cell atomic clock, ν _xtal is electronically tied to an atomic resonance, thereby transferring the stability of atomic structure to the clock’s tick rate.

The atomic resonance that forms the basis of the Rb clock’s operation is the transition between two hyperfine states of ⁸⁷Rb. As in hydrogen, the ground state of Rb is split into two hyperfine levels by the magnetic-dipole interaction between the single valence electron and the nucleus. Those states are labeled by the total-angular-momentum quantum number F, as shown in figure 1a. Each hyperfine state is further split into Zeeman sublevels, characterized by the quantum number m_F. The m_F = 0 sublevels are unaffected to first order by stray magnetic fields, which can arise in devices from a host of internal and environmental sources. The so-called 0–0 transition between the F = 2, m_F = 0 and F = 1, m_F = 0 states, with frequency ν _hfs = 6.8347 GHz, is unaffected by such fields and is ideal for stabilizing ν _xtal.

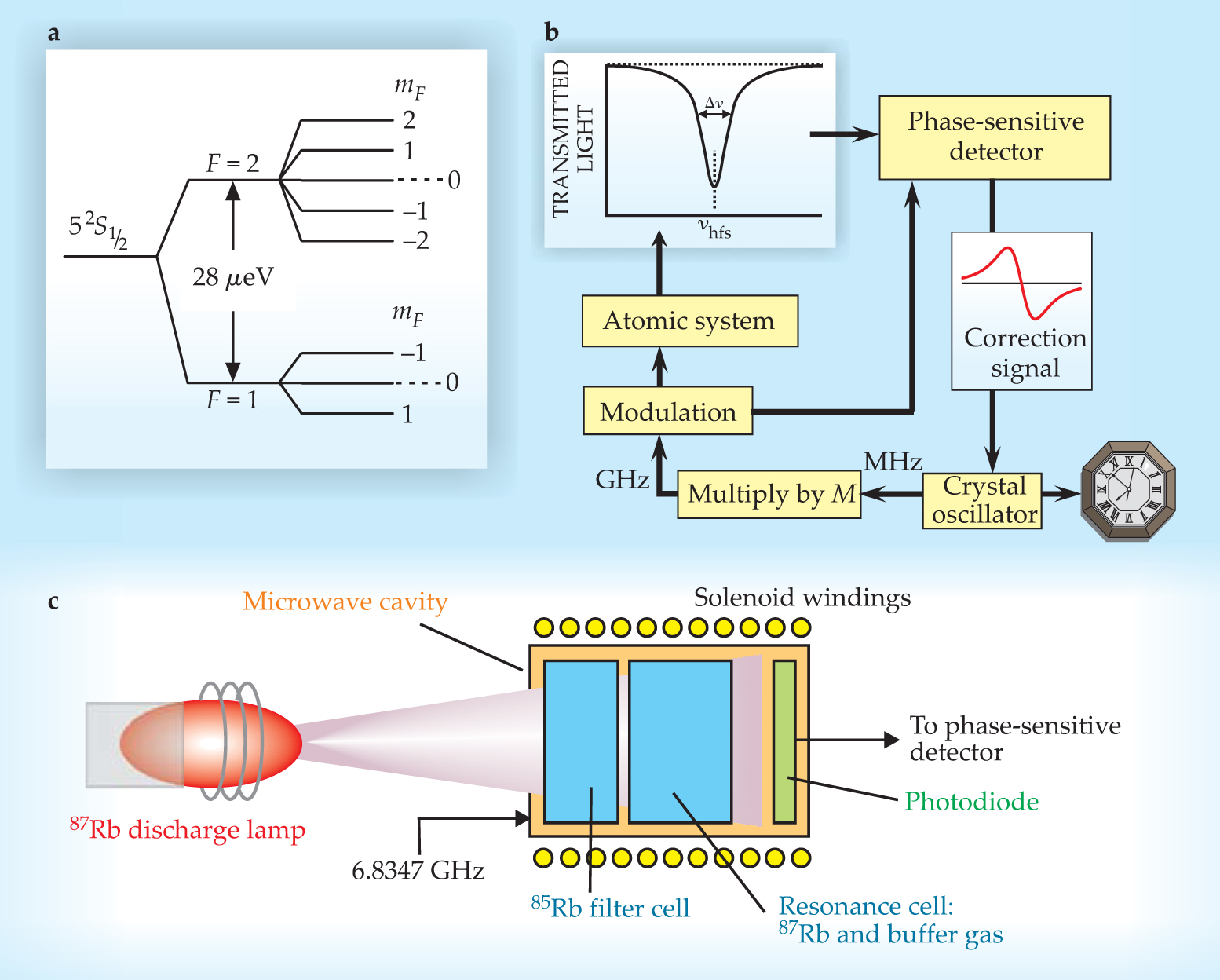
PTO.v60.i11.33_1.f1.jpg — **Figure 1. A generic rubidium** vapor-cell atomic clock. **(a)** The ground state of ⁸⁷Rb is split into two hyperfine levels, characterized by the quantum number F. The transition between the two m_F = 0 sublevels, unchanged to first order by stray magnetic fields, is used to stabilize a crystal oscillator’s frequency. **(b)** The frequency of a voltage-controlled crystal oscillator, scaled up by a factor M, is locked to the hyperfine-splitting frequency ν _hfs = 6.8347 GHz using phase-sensitive detection. The control voltage corrects the crystal oscillator’s frequency. **(c)** The clock’s atomic system consists of a few simple elements. ¹⁵ Optical pumping by lamplight creates a population imbalance between the hyperfine states of the ⁸⁷Rb atoms in the resonance cell, so that in steady state few atoms are in the F = 1 state and the transmitted light intensity is relatively high. When microwaves at ν _hfs are applied to the resonance cell, there is a net transfer of atoms from F = 1 back into F = 2 and a decrease in transmitted light intensity. The correction signal of the clock is proportional to the derivative of that microwave-induced resonant decrease in transmitted light intensity.
View larger

**Figure 1. A generic rubidium** vapor-cell atomic clock. **(a)** The ground state of ⁸⁷Rb is split into two hyperfine levels, characterized by the quantum number F. The transition between the two m_F = 0 sublevels, unchanged to first order by stray magnetic fields, is used to stabilize a crystal oscillator’s frequency. **(b)** The frequency of a voltage-controlled crystal oscillator, scaled up by a factor M, is locked to the hyperfine-splitting frequency ν _hfs = 6.8347 GHz using phase-sensitive detection. The control voltage corrects the crystal oscillator’s frequency. **(c)** The clock’s atomic system consists of a few simple elements. ¹⁵ Optical pumping by lamplight creates a population imbalance between the hyperfine states of the ⁸⁷Rb atoms in the resonance cell, so that in steady state few atoms are in the F = 1 state and the transmitted light intensity is relatively high. When microwaves at ν _hfs are applied to the resonance cell, there is a net transfer of atoms from F = 1 back into F = 2 and a decrease in transmitted light intensity. The correction signal of the clock is proportional to the derivative of that microwave-induced resonant decrease in transmitted light intensity.

Download

Figure 1b shows the means by which ν _xtal is electronically tied to ν _hfs. The first step is to multiply the output of a voltage-controlled crystal oscillator (VCXO) by a factor M to create a microwave field with a frequency near ν _hfs. The microwave field is frequency modulated, so that the ⁸⁷Rb atoms’ resonant absorption can be monitored by means of phase-sensitive detection. The detector’s output yields a correction voltage, proportional to the derivative of the resonance lineshape, which is used to adjust ν _xtal and lock it to ν _hfs. If ν _xtal is too low, the correction voltage is positive and ν _xtal increases; if ν _xtal is too high, a negative correction voltage is applied. Thus stabilized, the crystal oscillator’s frequency is used to keep time.

As illustrated in figure 1c, the atomic system of the clock consists of a ⁸⁷Rb discharge lamp, a ⁸⁵Rb-vapor filter cell, and a resonance cell containing ⁸⁷Rb vapor along with a buffer gas. Each element plays a role in generating the atoms’ response to the microwaves, and will be discussed further. For now, it suffices to note that the atoms’ resonant absorption of microwave radiation is manifested by a decrease in the transmitted light intensity. The resonance cell is located inside a microwave cavity, which in turn resides inside a solenoid. The solenoid’s magnetic field provides a quantization axis for the atoms, isolating the 0–0 transition. Moreover, since the 0–0 resonance has a second-order dependence on magnetic-field strength, the solenoid provides a convenient means of making slight adjustments to ν _hfs and thereby the clock’s frequency. (Though ν _hfs may be stable, it can be slightly inaccurate due to various atomic perturbations and in need of calibration.)

Optical pumping and the light shift

Without a population imbalance between the ⁸⁷Rb hyperfine states, there can be no net absorption of microwaves by the atoms in the resonance cell: The rate of photons leaving the field through absorption would be counterbalanced by the rate of stimulated emission repopulating the field. For ⁸⁷Rb, the hyperfine-energy-level separation is only 28 μeV, whereas gas-phase kinetic energies are approximately 40 meV. Thus, under normal conditions, the vapor-phase atoms populate both hyperfine manifolds equally. The system for creating the necessary population imbalance is a direct outgrowth of the Nobel Prize–winning work of Alfred Kastler, who showed that light can create a nonthermal population distribution among atomic energy levels in a process known as optical pumping. ¹

As illustrated in figure 2, a ⁸⁷Rb discharge lamp emits light at frequencies that connect Rb’s excited states with each ground-state hyperfine level. Due to a coincidence of nature, spectral lines associated with ⁸⁷Rb’s F = 2 state are nearly degenerate with those of ⁸⁵Rb’s F = 3 state. Thus, as Peter Bender and colleagues explained in a 1958 Physical Review Letter, ² a filter of ⁸⁵Rb vapor can remove the F = 2 spectral component from a ⁸⁷Rb lamp’s emission. When the filtered lamplight reaches the ⁸⁷Rb atoms in the resonance cell, it preferentially excites atoms out of the F = 1 state. Decay from the excited state repopulates both hyperfine levels, but those atoms returning to the F = 1 state are excited again, so that after several absorption–decay cycles a nonthermal population distribution is created. The easy filtering of lamplight is the primary reason present-day vapor-cell clocks use Rb instead of other alkali metals.

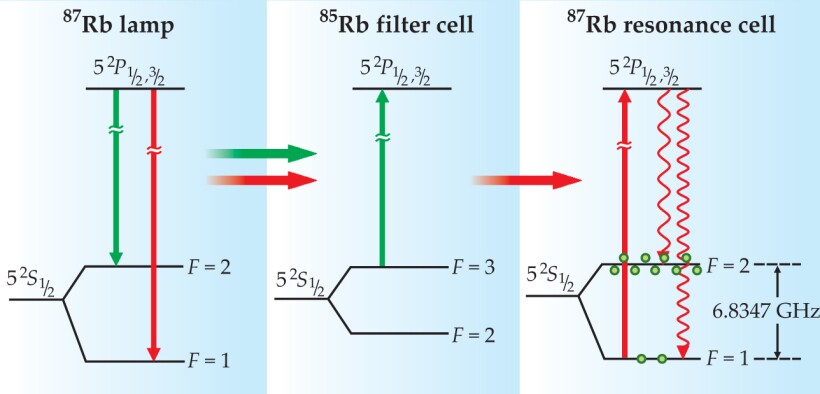
PTO.v60.i11.33_1.f2.jpg — **Figure 2. The rubidium-87 lamp** emits light at frequencies associated with both hyperfine states: There are two fluorescence lines from the 5² P _1/2 state of wavelength 795 nm and two fluorescence lines from the 5² P _3/2 state of wavelength 780 nm. Each pair of lines is separated by approximately 0.014 nm. Due to a coincidence of nature, the spectral lines associated with ⁸⁷Rb’s F = 2 state are absorbed by ⁸⁵Rb atoms; the other lamp lines are unaffected. When the filtered lamplight passes into the resonance cell, several cycles of optical absorption and emission create a population imbalance between the F = 2 and F = 1 states.
View larger

**Figure 2. The rubidium-87 lamp** emits light at frequencies associated with both hyperfine states: There are two fluorescence lines from the 5² P _1/2 state of wavelength 795 nm and two fluorescence lines from the 5² P _3/2 state of wavelength 780 nm. Each pair of lines is separated by approximately 0.014 nm. Due to a coincidence of nature, the spectral lines associated with ⁸⁷Rb’s F = 2 state are absorbed by ⁸⁵Rb atoms; the other lamp lines are unaffected. When the filtered lamplight passes into the resonance cell, several cycles of optical absorption and emission create a population imbalance between the F = 2 and F = 1 states.

Download

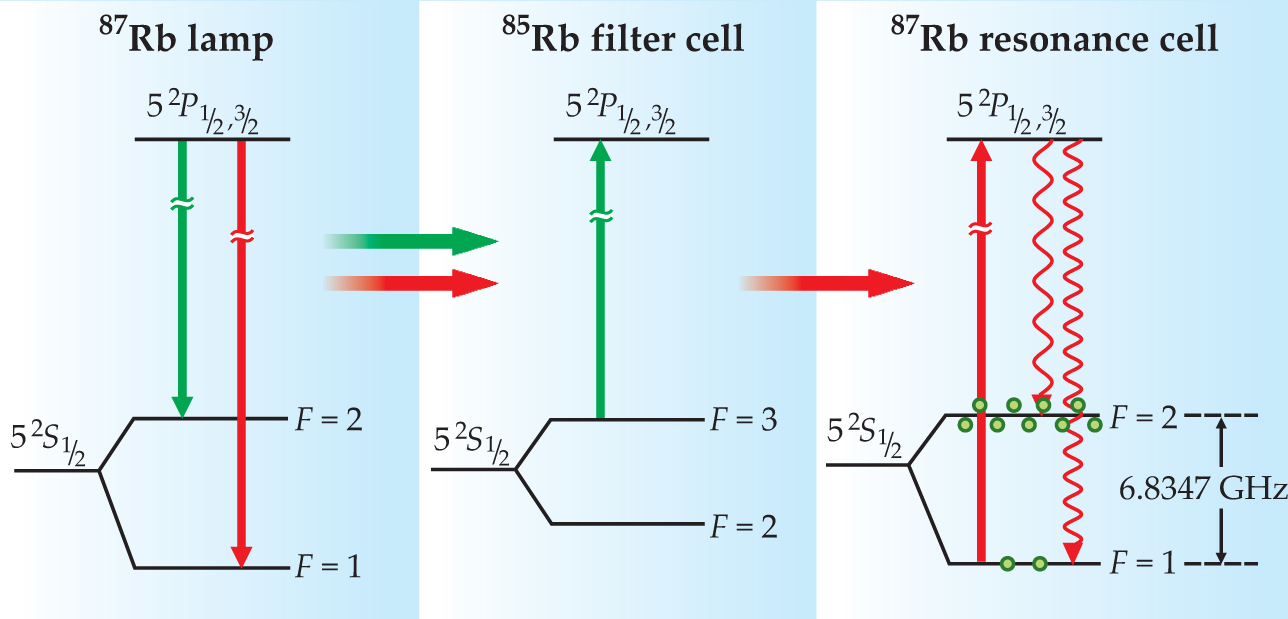
The discharge lamp not only drives the optical-pumping process but also provides a signal that indicates when the microwave field is on resonance with the 0–0 transition. When the field is off resonance, there are few atoms in the F = 1 state, so most of the lamplight passes through the resonance cell unabsorbed. But when the microwave frequency equals ν _hfs, the atoms return to the F = 1 state, and the intensity of transmitted lamplight measured by the photodiode decreases.

Unfortunately, the lamplight in the resonance cell perturbs Rb’s energy-level structure. Due to the so-called light shift, discussed in box 1, ν _hfs depends on both the intensity and the spectral profile of the lamplight. For example, a 1% change in lamp intensity can shift the hyperfine energy level spacing (and thus the clock’s frequency) by one part in 10¹². That shift may seem small, but it can result in positioning errors on the order of tens of meters in satellite navigation systems. Over the years, understanding the mechanism of the light shift and the different ways it affects clock stability has been an active area of basic and applied research. Investigators have developed quantum-field and semiclassical light-shift theories, explored the implications of those theories for the field–atom interaction, ³ studied how the reabsorption of fluorescent photons by atoms in the lamp affects the lamp’s spectral emission, ⁴ and examined the spatial variation of ν _hfs in the resonance cell due to the exponential attenuation of the lamplight. ⁵

The role of the buffer gas

The key to generating a correction signal for the crystal oscillator is to get the ⁸⁷Rb atoms in the resonance cell to absorb microwave radiation in a narrow frequency band around ν _hfs. Since the efficacy of the correction signal is measured by the instability of the crystal oscillator’s frequency, given by (Δν/ν _hfs)/(S/N), an atomic transition with a high signal-to-noise ratio S/N and a narrow linewidth Δν results in the best performance (see the article by James Bergquist, Steven Jefferts, and David Wineland, Physics Today, March 2001, page 37 ).

The resonance cell of a Rb clock contains not only ⁸⁷Rb vapor at a pressure of 10⁻² Pa but also a buffer-gas mixture of nitrogen and a noble gas, with a total pressure of about 10³ Pa. The buffer gas plays several roles, two of which are directly related to the transition linewidth.

In 1953 Robert Dicke wrote a two-page paper in Physical Review that set the stage for vapor-cell clock development. ⁶ As described in box 2, when an atom is confined to a region of space smaller than the field’s wavelength, Doppler broadening is eliminated. Since buffer-gas collisions ensure that mean free paths are much less than the wavelength that corresponds to ν _hfs (4.4 cm for ⁸⁷Rb), Dicke’s criterion is easily satisfied; and rather than 10-kHz Doppler-broadened lines, 0–0 transition linewidths are on the order of 10²Hz.

In modern vapor-cell clocks, however, the buffer-gas pressure is thousands of times larger than what is needed for Dicke narrowing. One reason for the higher pressure is to protect the Rb atoms from collisions with the bare glass walls of the resonance cell. Narrow atomic resonances require not only the elimination of Doppler broadening, but also a long coherence time T ₂, where Δν ~ 1/T ₂. When a ⁸⁷Rb atom absorbs microwaves, its wavefunction becomes a superposition of the F = 1 and F = 2 states, and for narrow resonances, the superposition state’s phase must remain constant for long periods of time. Unfortunately, when an atom collides with a bare glass wall, the superposition state’s phase is randomized, so T ₂ is limited by the atom’s flight time across the resonance cell. A collision with a molecule of N₂ or noble gas, however, only weakly affects the superposition state’s phase. Consequently, the high-pressure buffer gas can slow the diffusion of Rb atoms to the glass walls without appreciably affecting the superposition state’s phase, and thereby lengthen T ₂.

To say that a buffer-gas atom or molecule only weakly affects the superposition state’s phase camouflages a great deal of complicated physics, and interest in the effects of buffer-gas collisions on the 0–0 transition’s linewidth motivated considerable research in the 1960s and 1970s. Today it continues to influence basic research as the need for better clocks motivates a deeper understanding of the interaction between buffer-gas species and alkali-metal atoms. As an example, William Happer and his colleagues have recently studied binary collisions between Rb and noble-gas atoms ⁷ and have discovered that collisional changes in electron density at the alkali nucleus can be important in limiting T ₂.

The other reason for relatively high buffer-gas pressure has to do with the efficiency of optical pumping. An isolated Rb atom, after excitation by the lamplight, returns to the ground state by emitting a fluorescent photon. Alkali metals, however, are notorious for reabsorbing their fluorescent photons in a process known as radiation trapping, which has the effect of undoing the optical-pumping effect of the lamp-light. ⁸ It’s as if there were an extra source of light in the resonance cell that could excite atoms out of the ⁸⁷Rb F = 2 hyperfine level. But radiation trapping can be avoided with the addition of N₂ as a buffer gas. When a Rb atom collides with a molecule of N₂, Rb electronic energy is converted into N₂ vibrational energy, and the Rb atom returns to its ground state without fluorescing. In a very real sense, efficient optical pumping in the vapor-cell clock relies on the chemical physics of intermolecular energy transfer.

The light shift

The light shift is one of the earliest known manifestations of what is today generally known as the AC Stark shift, and it can be understood as a consequence of energy conservation. ¹⁶ Consider a three-level atom interacting with an optical field of frequency ω that drives the |2〉 → |3〉 transition. Suppose that in the absence of the field–atom interaction there are N photons in the field, so that the total energy of the field–atom system is E ₂ + Nℏω. With the interaction turned on and the field off resonance, the atom spends a fraction f of its time in state |3〉, and states |2〉 and |3〉 are shifted in opposite directions by an amount δν _LS. Conservation of energy then requires that

$\begin{matrix} E_{2} + N ħ ω = (1 - f) [E_{2} - ħ δ ν_{LS} + N ħ ω] + \\ f [E_{2} + ħ ω_{0} + ħ δ ν_{LS} + (N - 1) ħ ω], \end{matrix}$ (1)

from which it follows that δν _LS = f(ω ⁰ – ω)/(1 − 2f).

The parameter f can be determined from a rate-equation model of the interaction process involving the Einstein A and B coefficients: f = Bρg(ω)/[A + 2Bρg(ω)], where ρ is the energy density of the field and g(ω) corresponds to the optical transition’s lineshape. Without going into the details, it can be shown that

$δ ν_{LS} ~ \frac{I (ω_{0} - ω)}{{(ω_{0} - ω)}^{2} + Γ^{2}},$ (2)

where I is the intensity of the optical field and Γ is the optical transition linewidth. The shift in the energy of |2〉 causes a change in the |1〉 ↔ |2〉 energy-level spacing, which is detected as a light-induced change in ν _hfs.

The AC Stark shift is fundamentally related to the Lamb shift, which arises from an atom’s interaction with the vacuum. The light shift arises from real photons driving virtual transitions in an atom (that is, ω ≠ ω ₀); the Lamb shift arises from virtual photons driving virtual transitions in an atom. The relationship was not lost on the original investigators, and in a play on words Alfred Kastler suggested renaming the phenomenon the Lamp shift. ¹⁷ In fact, in cavity quantum electrodynamics experiments it may be difficult to disentangle the two phenomena. ¹⁸

PTO.v60.i11.33_1.d1.jpg

Dicke narrowing

Consider the one-dimensional problem of a radiating atom of mass m confined to a square well of infinite depth and width L. In a quantized theory of radiation, the Doppler effect is a consequence of momentum conservation between the radiating atom and the emitted photon observed in the laboratory frame. Energy conservation between the initial and final states gives

$\frac{1}{2} m v_{i}^{2} + (E_{e} - E_{g}) = \frac{1}{2} m v_{f}^{2} + \frac{h c}{λ_{emit}},$ (1)

where E _e and E _g are the excited-state and ground-state energies, v _i and v _f are the initial and final velocities, and λ _emit is the wavelength of the emitted photon. Momentum conservation gives

$m v_{i} = m v_{f} \pm \frac{h}{λ_{emit}},$ (2)

where the ± sign refers to the emitted photon’s direction relative to v _i. Combining equations 1 and 2 gives the textbook nonrelativistic expression for the Doppler shift of the emitted photon in terms of the rest-frame transition wavelength λ ⁰ = hc/(E _e – E _g):

$\frac{λ_{emit} - λ_{0}}{λ_{0}} = \mp \frac{v_{i}}{c} .$ (3)

Because the atom is confined to a square well, however, its momentum is quantized and can only change in units of h/2L. If the photon’s momentum is smaller than that (that is, λ _emit/2L > 1), then the atom’s momentum state cannot change following photon emission. In such cases the field–atom interaction must be viewed in the broader context of energy and momentum conservation for the atom–potential-well system. The emitted photon’s momentum is then transferred to the potential well, which presumably has infinite mass, so that the atom’s velocity remains unchanged and the Doppler shift is zero.

PTO.v60.i11.33_1.d2.jpg

State of the art

The best Rb clocks ever built are now flying on GPS satellites. Those clocks are so stable that in three hours they accrue less than half a nanosecond of time error. In the same three hours, general relativistic effects due to the satellite’s elevated location, if left uncorrected, would cause a satellite clock and a terrestrial clock to accrue a little more than 5 microseconds of time offset. In other words, GPS Rb atomic clocks can sense those general relativistic effects at the fourth significant figure. (See the article by Neil Ashby, Physics Today, May 2002, page 41 .)

Rubidium clocks aboard satellites operate under different conditions than do terrestrial clocks, and the need to adapt the clocks to those conditions has led to a range of physical and chemical research. For example, the inner glass surface of a discharge lamp experiences a harsh environment, with energetic ions etching the surface and alkali-metal atoms chemically interacting with the exposed glass. If that chemistry were to lead to lamp failure in a terrestrial clock, one would simply ship the device back to the manufacturer for a replacement lamp. However, no one services a failed clock on a GPS satellite, so the lamps must operate unattended and reliably throughout the satellite’s many-year mission. In the 1980s the question of a lamp’s lifetime motivated Robert Frueholz and his colleagues at The Aerospace Corporation to study alkali–glass physical chemistry. ⁹ Frueholz and colleagues used electron spectroscopy and secondary-ion mass spectrometry to show that Rb forms an oxide on the lamp’s inner glass surface and penetrates into the glass matrix, quite likely taking the form of a rubidium silicate. The complete depletion of Rb through those mechanisms would lead to a lamp’s failure. Using differential scanning calorimetry, the researchers then determined the rates at which various glass types consume Rb. As a result of their work, clock manufacturers can now determine how much liquid Rb needs to be deposited into a lamp to guarantee its operation over any specified mission lifetime.

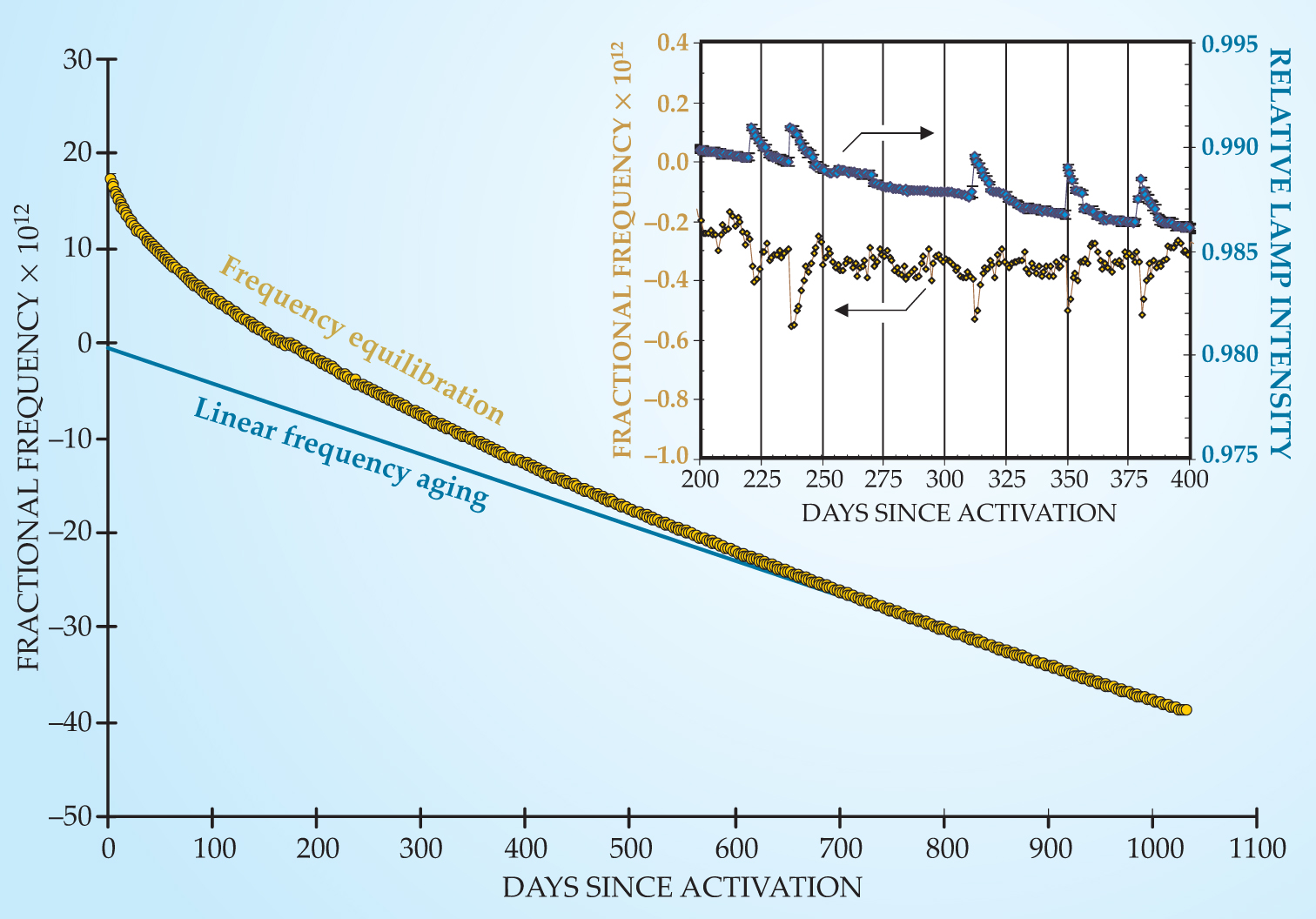
An important area of current research concerns the slow changes in a clock’s frequency over time. Figure 3 shows the frequency variations of a GPS satellite clock after it was turned on; its general characteristics are common to all rubidium clocks. Following activation the clock experienced a very slow exponential equilibration until it settled down to a linear frequency change with time. The mechanisms that drive those two processes are not yet understood. ¹⁰ The figure’s inset shows an expanded view around days 200 to 400, illustrating several slight frequency jumps that are correlated with small changes in the lamp’s output. There, the influence of the light-shift effect is evident—the intensity of lamplight in the resonance cell directly affects the clock frequency—but the cause of those small lamp changes is not yet known. Though not shown in the figure, the frequency of every Rb clock undergoes slight stochastic fluctuations. In the long term, those fluctuations correspond to Brownian-type motion, and again the physical process that drives them is not understood. Clearly, although the Rb clock has been studied for 50 years, much remains to be understood and improved.

PTO.v60.i11.33_1.f3.jpg — **Figure 3. Reconstructed frequency history** of a rubidium atomic clock aboard a GPS satellite. Two phenomena contribute to the long-term frequency variations: slow exponential frequency equilibration, with a time constant of 235 days, and linear frequency aging at a rate of 3.7 × 10⁻¹⁴/day. It is not known whether the phenomena are driven by the same physical mechanism. The inset shows clock frequency jumps arising from the light shift (see box 1).
View larger

**Figure 3. Reconstructed frequency history** of a rubidium atomic clock aboard a GPS satellite. Two phenomena contribute to the long-term frequency variations: slow exponential frequency equilibration, with a time constant of 235 days, and linear frequency aging at a rate of 3.7 × 10⁻¹⁴/day. It is not known whether the phenomena are driven by the same physical mechanism. The inset shows clock frequency jumps arising from the light shift (see box 1).

Download

The laser-pumped vapor-cell clock

It likely seems old-fashioned to use discharge lamps when semiconductor lasers are so readily available. Shouldn’t it be a simple matter to replace the lamp and filter cell with a diode laser and significantly increase the efficiency of optical pumping and hence the clock signal? That was the thinking of researchers in the mid-1980s, who anticipated that the use of diode lasers would lead to great improvements in clock stability and better control of the light shift. Unfortunately, that happy situation was not so easily realized: Optical pumping with diode lasers did produce a 10-fold increase in clock-signal amplitude, but it also produced a 100-fold increase in the noise. Thus, with an overall reduction in signal-to-noise ratio, the first diode-laser-pumped vapor-cell clocks had poorer frequency stability.

That puzzling situation motivated research into what may best be called the stochastic field–atom interaction problem. No real-world electromagnetic field corresponds to the textbook monochromatic field, and random fluctuations in a field’s phase and intensity can alter the nature of the field–atom interaction in qualitative and quantitative ways. In the case of the laser-pumped clock, researchers discovered that the basic light–matter interaction converts a field’s phase noise into absorption cross-section fluctuations, which, in turn, produce noise in the transmitted laser intensity. ¹¹ That problem was particularly severe with the cleaved-facet diode lasers used in the early studies, since, as bad luck would have it, their noise characteristics were optimal for converting phase noise into intensity noise.

Once the noise-enhancement process was understood, efforts turned toward mitigation strategies, which have largely proved effective: Either one can use diode lasers with narrow linewidths, which have low phase noise, or one can increase the buffer-gas pressure in the resonance cell to 10⁴ Pa to make the atoms less sensitive to the field’s phase fluctuations. At high buffer-gas pressures, the frequent ⁸⁷Rb–buffer collisions interrupt the alkali atoms as they attempt to follow the laser’s fluctuating phase, so that the Rb vapor responds to the average laser phase instead of its instantaneous variations.

Although research into the stochastic field–atom interaction and its implications for clock performance continues, ¹² investigators’ attention has also turned to the light shift. Not only does the multilevel nature of real atoms complicate the light shift, but in a laser-pumped clock the laser frequency is typically modulated in order to actively lock the laser to the atom’s absorption. That leads to a modulation of ν _hfs, which can affect the clock’s stability. Understanding and controlling the light shift, and mitigating its deleterious effects on laser-pumped clock performance, is an active area of research.

Interfering pathways of excitation

Consider a three-level atom interacting with a bimodal electric field $E (t) = E_{0} [cos (ω_{a} t) + cos (ω_{b} t + φ)]$ that couples states |1〉 and |2〉, two hyperfine levels split by ν _hfs, to state |3〉. The atomic wavefunction φ can be expanded in terms of the unperturbed eigenstates—that is,

$Φ = Σ_{n = 1}^{3} c_{n} | n 〉 e^{- i ω_{n} t} .$ (1)

Shortly after the field is turned on, $c_{1} = c_{2} = 1 / \sqrt{2,}$ , and it can be shown by time-dependent perturbation theory that

${\dot{c}}_{3} = - \frac{i e E_{0}}{\sqrt{2 ħ}} (r_{31} + r_{32} e^{i φ}),$ (2)

where r_mn = 〈m|r|n〉, the first e is the electron charge, the second e is the natural logarithm base, and φ is the phase difference between the two components of the field. The probability P ₃ of finding the atom in state |3〉 is simply |c ₃|², and can be found by integrating equation 2:

$P_{3} (t) = \frac{t^{2}}{2} {(\frac{e E_{0}}{ħ})}^{2} ({| r_{31} |}^{2} + {| r_{32} |}^{2} + r_{31} r_{32}^{•} e^{- i φ} + r_{31}^{•} r_{32} e^{i φ}) .$ (3)

In the case where r ₃₂ = r ₃₁ e ^iθ, so that those two matrix elements differ only in phase, equation 3 can be simplified:

$P_{3} (t) = t^{2} {(\frac{e E_{0}}{ħ})}^{2} {| r_{31} |}^{2} [1 + cos (φ + θ)] .$ (4)

If the phase of the field’s b mode varies rapidly and randomly with respect to the a mode, then the cosine term of equation 4 averages to zero, and each excitation pathway acts independently. Alternatively, if φ + θ = 0, then the two excitation pathways interfere constructively, and the probability of exciting the atom is enhanced. If, however, φ + θ =π, then the two excitation pathways interfere destructively, and P ₃ = 0 even though both field components resonantly interact with the atom. The latter situation is typical for the coherent-population-trapping clock: The intensity of light transmitted by the vapor shows a resonant increase when the mode spacing equals ν _hfs. The CPT phenomenon is intimately associated with electromagnetically induced transparency. (See the article by Stephen Harris, Physics Today, July 1997, page 36 .)

PTO.v60.i11.33_1.d3.jpg

The chip-scale atomic clock

The coherent-population-trapping atomic clock is a radical departure from the traditional vapor-cell clock, and whether that will prove to be advantageous is an open question of great interest. With the CPT clock, the signal is generated in an all-optical fashion: ¹³ The laser field is modulated at a frequency near ν _hfs/2, derived from a harmonic of ν _xtal, to produce sidebands in the laser spectrum above and below the unperturbed laser frequency. When the separation between the sidebands equals ν _hfs, both hyperfine levels are simultaneously coupled to the same excited state. The two excitation pathways then interfere destructively (see box 3), leading to reduced absorption of laser light, and that signal is used to lock ν _xtal to ν _hfs. The most striking feature of the CPT clock is that the microwave cavity is eliminated, which allows a great reduction in size and, as illustrated in figure 4, a push for truly chip-scale devices. ¹⁴ Though questions regarding the stochastic field–atom interaction are as relevant for the CPT clock as they are for the traditional laser-pumped clock, research to date has focused on the more pressing issue of achieving chip-scale dimensions at low power without sacrificing short-term frequency stability.

PTO.v60.i11.33_1.f4.jpg — **Figure 4. The proverbial black box** (left) is a commercial lamp-pumped rubidium clock. On the right is the physics package of a coherent-population-trapping chip-scale atomic clock developed at NIST, which contains the laser, optics, resonance cell with alkali vapor and buffer gas, and photodetector.

(Chip-scale clock image from ref. 14.)
View larger

**Figure 4. The proverbial black box** (left) is a commercial lamp-pumped rubidium clock. On the right is the physics package of a coherent-population-trapping chip-scale atomic clock developed at NIST, which contains the laser, optics, resonance cell with alkali vapor and buffer gas, and photodetector.
(Chip-scale clock image from ref. 14.)

Download

Independent of size, there is another, less tangible motivation for CPT clock research. As discussed in connection with figure 3, researchers have much to learn about vapor-cell clock physics. Perhaps having two qualitatively different manifestations of a vapor-cell clock will provide a point of comparison that can illuminate the origins of frequency equilibration, frequency aging, and random-walk frequency noise. That such a comparison will prove fruitful is, unfortunately, not guaranteed. The only certain conclusion is that the technological drive to develop vapor-cell clocks for diverse applications will continue to motivate atomic and chemical physics research well into the 21st century. And without that close connection between basic research and technological innovation, it would be much harder to find your way to the airport on a dark rainy night when you’re lost.

I thank The Aerospace Corporation for support under the Mission-Oriented Investigation and Experimentation program, funded by US Air Force Space and Missile Systems Center under contract FA8802-04-C-0001.

References

1. A. Bloom, Sci. Am. 203, 72 (1960); https://doi.org/10.1038/scientificamerican1060-72
W. Happer, W. van Wijngaarden, Hyperfine Interact. 38, 435 (1987). https://doi.org/10.1007/BF02394855
2. P. Bender, E. Beaty, A. Chi, Phys. Rev. Lett. 1, 311 (1958). https://doi.org/10.1103/PhysRevLett.1.311
3. W. Happer, Light Propagation and Light Shifts in Optical Pumping Experiments, Pergamon, New York (1970), p. 51.
4. J. Camparo, R. Mackay, J. Appl. Phys. 101, 053303 (2007). https://doi.org/10.1063/1.2435914
5. J. Camparo, R. Frueholz, C. Volk, Phys. Rev. A 27, 1914 (1983). https://doi.org/10.1103/PhysRevA.27.1914
6. R. Dicke, Phys. Rev. 89, 472 (1953). https://doi.org/10.1103/PhysRev.89.472
7. D. K. Walter, W. M. Griffith, W. Happer, Phys. Rev. Lett. 88, 093004 (2002); https://doi.org/10.1103/PhysRevLett.88.093004
P. Oreto et al., Phys. Rev. A 69, 042716 (2004). https://doi.org/10.1103/PhysRevA.69.042716
8. J. C. Camparo, S. B. Delcamp, Opt. Commun. 120, 257 (1995). https://doi.org/10.1016/0030-4018(95)00426-9
9. R. Frueholz, M. Wun-Fogle, J. Am. Ceram. Soc. 66, 605 (1983); https://doi.org/10.1111/j.1151-2916.1983.tb10606.x
R. Cook, R. Frueholz, Proceedings of the 42nd Annual Frequency Control Symposium, IEEE, Piscataway, NJ (1988), p. 525. https://doi.org/10.1109/FREQ.1988.27651
10. J. Camparo, C. Klimcak, S. Herbulock, IEEE Trans. Instrum. Meas. 54, 1873 (2005); https://doi.org/10.1109/TIM.2005.853217
J. Coffer, B. Sickmiller, J. Camparo, IEEE Trans. Ultrason. Ferroelectr. Freq. Control 51, 139 (2004); https://doi.org/10.1109/TUFFC.2004.1320761
J. Camparo, IEEE Ultrason. Ferroelectr. Freq. Control 52, 1075 (2005). https://doi.org/10.1109/TUFFC.2005.1503993
11. J. Camparo, J. Coffer, Phys. Rev. A 59, 728 (1999); https://doi.org/10.1103/PhysRevA.59.728
J. Coffer, M. Anderson, J. Camparo, Phys. Rev. A 65, 033807 (2002). https://doi.org/10.1103/PhysRevA.65.033807
12. J. J. Townsend, J. G. Coffer, J. C. Camparo, Phys. Rev. A 72, 033807 (2005); https://doi.org/10.1103/PhysRevA.72.033807
M. Huang, J. G. Coffer, J. C. Camparo, Opt. Commun. 265, 187 (2006). https://doi.org/10.1016/j.optcom.2006.03.004
13. J. Vanier, Appl. Phys. B 81, 421 (2005). https://doi.org/10.1007/s00340-005-1905-3
14. S. Knappe et al., Appl. Phys. Lett. 85, 1460 (2004). https://doi.org/10.1063/1.1787942
15. J. Vanier, C. Audoin, The Quantum Physics of Atomic Frequency Standards, Adam Hilger/IOP, Bristol, UK (1989), chap. 3. https://doi.org/10.1887/085274434X
16. J. Bjorkholm, P. Liao, Lecture Notes in Physics: Volume 43, Springer, Berlin (1975), p. 176. https://doi.org/10.1007/3-540-07411-2_272
17. A. Kastler, J. Opt. Soc. Am. 53, 902 (1963). https://doi.org/10.1364/JOSA.53.000902
18. J. Camparo, P. Lambropoulos, J. Opt. Soc. Am. B 19, 1169 (2002). https://doi.org/10.1364/JOSAB.19.001169

More about the Authors

James Camparo is a senior scientist at The Aerospace Corporation in Los Angeles.

James Camparo. Aerospace Corporation, Los Angeles, US .