The Aharonov–Bohm effects: Variations on a subtle theme
DOI: 10.1063/1.3226854
Quantum phenomena that were once thought to limit measurement capabilities are now being harnessed to enhance them and to improve the sensitivity of nanometer-size devices. Persistent questioning and probing of quantum phenomena has yielded many such advances. However, the Aharonov-Bohm effect, a modern cornerstone of quantum mechanics, is not yet a good example of that kind of progress. The AB effect was already implicit in the 1926 Schrödinger equation, but it would be another three decades before theorists Yakir Aharonov and David Bohm pointed it out. 1 And to this day, the investigation and exploitation of the AB effect remain far from finished.
Our discussion of the AB effect begins with a seemingly innocent question: What happens to an electron as it passes by an infinitely long ideal solenoid? One might expect that the electron is unaffected. Outside the solenoid, the magnetic and electric fields B and E, and thus the Lorentz force, are all zero. But in quantum mechanics one describes an interaction not by the forces involved but rather by the Hamiltonian.
The canonical momentum in the electromagnetic Hamiltonian has a term proportional to the magnetic vector potential A, which is defined (with some gauge freedom) by B = ∇ × A. Before the AB paper, the vector potential was generally thought of as a useful mathematical artifice without independent physical reality. Aharonov and Bohm changed all that.
The first interesting fact is that A is not zero outside the solenoid, even though the force fields E and B vanish there (see figure 1). The vector potential is everywhere azimuthal to the solenoid’s axis, and Stokes’s theorem says that its line integral around any loop enclosing the solenoid equals the magnetic flux Φ inside. So outside the solenoid, A falls off like 1/r with distance r from the axis.

Figure 1. Two electrons passing by a long current-carrying solenoid on opposite sides (along the blue trajectories) illustrate the magnetic Aharonov-Bohm effect. Although the solenoid’s magnetic field (purple flux lines) is almost entirely restricted to the coil’s interior, the vector potential A outside (tangential to the green coaxial circles) falls off only as 1/r with distance r from the axis. One of the two trajectories is parallel to A (at the point of closest approach), while the other is antiparallel. Even in the absence of any Lorentz force on the electrons, that difference produces a quantum mechanical phase shift between their wavefunctions.
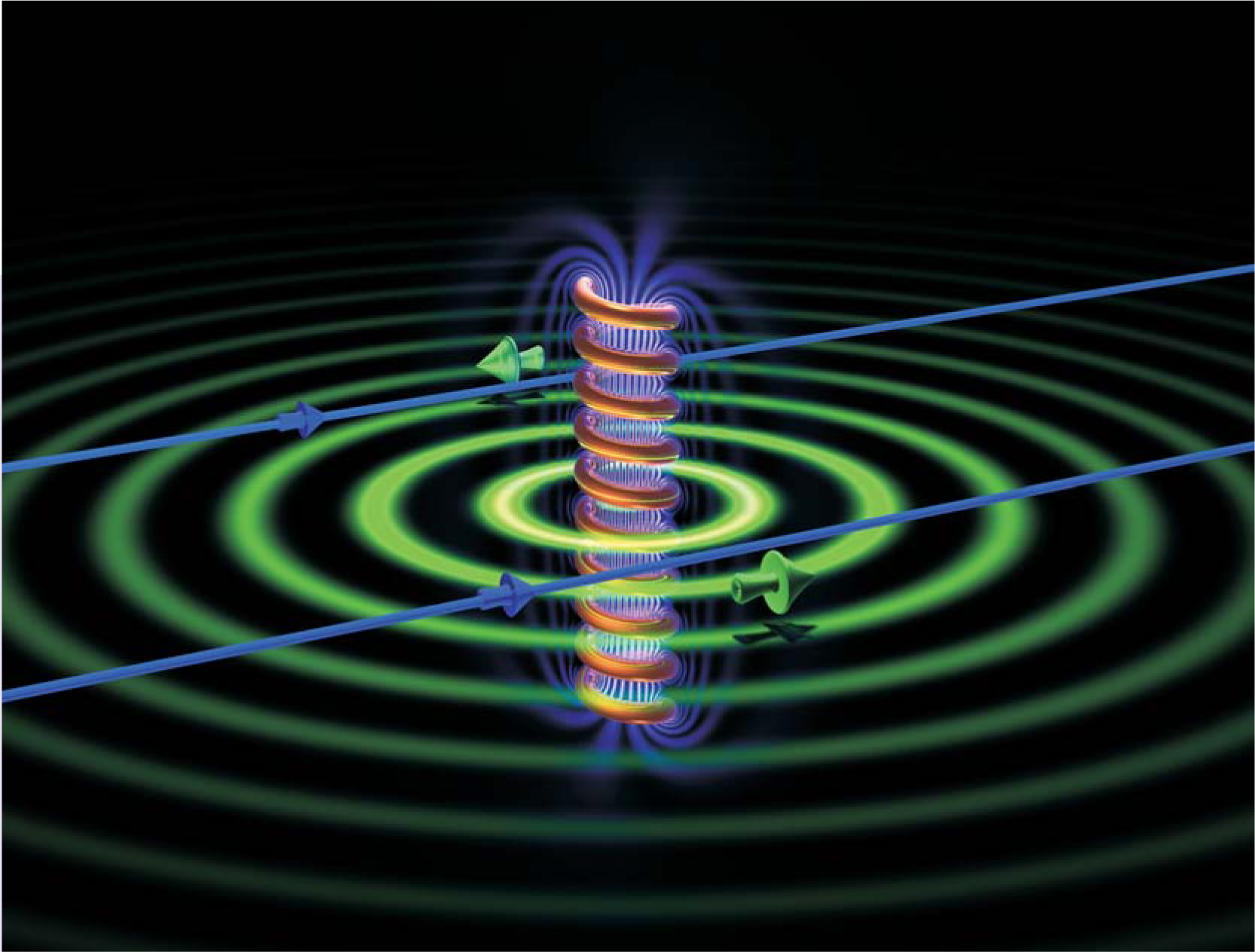
In figure 1, two electrons traveling together pass by the solenoid on opposite sides. At the points of closest approach to the solenoid, one is traveling parallel to A on its side, the other antiparallel. Quantum mechanically, one says that the electrons interact with the solenoid because the wavefunction of each accumulates a phase shift
as it traverses the vector potential.
The dot product in equation
known as the magnetic Aharonov–Bohm phase shift.
In 1959, beyond pointing out that quantum mechanics implied this phase shift in the absence of any classical force, Aharonov and Bohm suggested how it could be measured by having electron waves traversing the two paths interfere with each other. And so, indeed, was the AB phase shift soon confirmed in the laboratory. 2 Achieving interference patterns requires that the initial electron beam be adequately coherent and that its splitting maintain that coherence. The former is accomplished by having a well-collimated beam with narrow spreads in angle and particle energy, and the latter requires something like a diffraction grating or an electromagnetic biprism. 3
A heuristic example makes the existence of the AB phase shift less surprising and elucidates the classical–quantum correspondence. Figure 2 shows the constant-phase wave-front of a coherent electron beam passing through and around a magnetized bar with a homogeneous magnetic field. The electrons actually traversing the bar are deflected by the Lorentz force, and that part of the wavefront is correspondingly tilted. The wavefront for those parts of the beam that pass outside the bar remains untilted. But continuity requires the entire phase-constant wavefront to remain contiguous, so that one of its undeflected segments now lags the other, and a proper cross section of the beam shows a corresponding phase shift between electrons that passed undeflected on opposite sides of the bar.

Figure 2. Semiclassical argument for the magnetic Aharonov–Bohm effect. Consider the plane wavefront of a coherent electron beam passing through and around a uniformly magnetized bar. Electrons going through the bar are deflected by the Lorentz force, tilting their sector of the wavefront. Electrons passing outside the bar see no magnetic field, so their sectors remain untilted. But because continuity requires the three sectors of the constant-phase front to remain contiguous, the two untilted sectors are now displaced along the beam direction, which implies a corresponding phase shift across a cross section of the beam. The phase shift thus calculated in terms of the Lorentz force is the same as that predicted by the AB effect in terms of the vector potential A circling the bar.
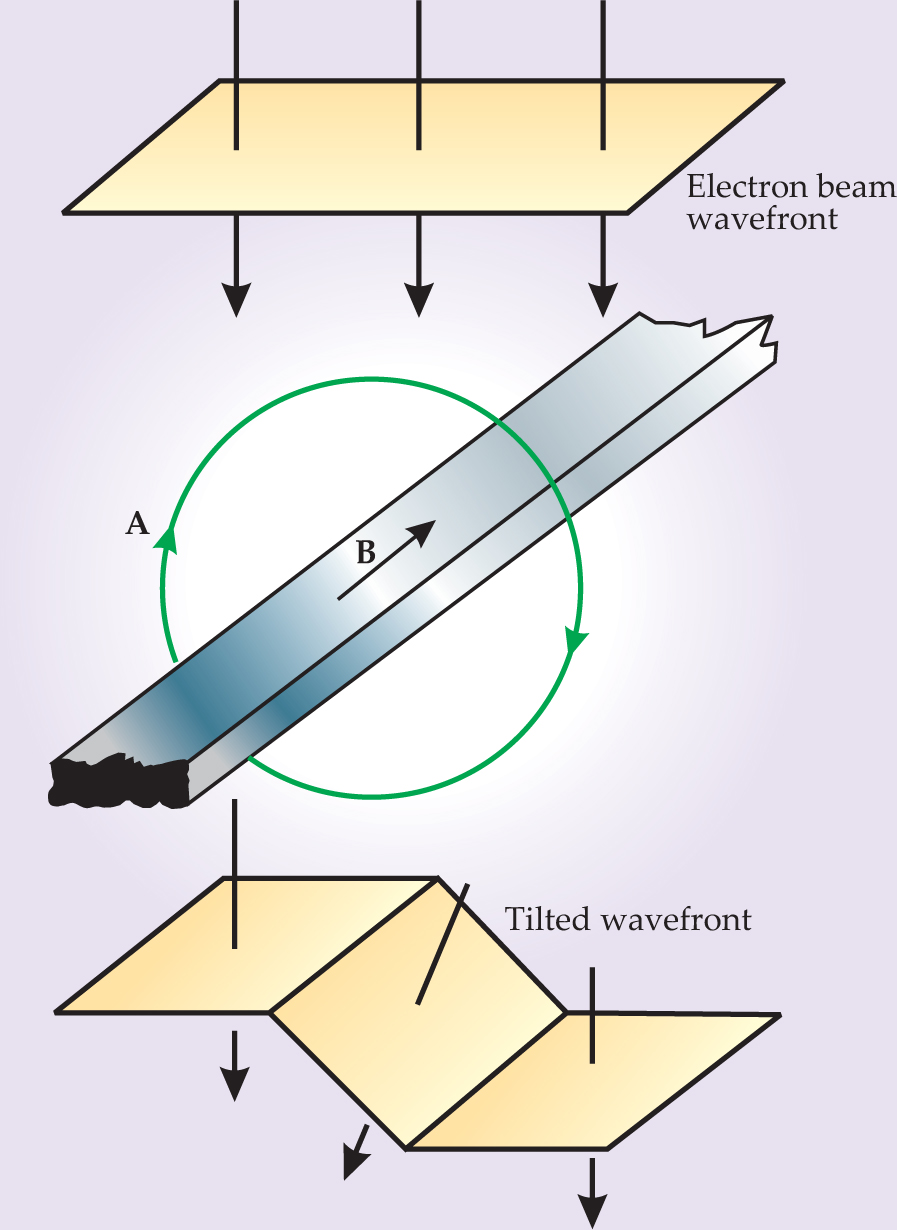
Following through that simple semiclassical picture, one gets the same phase shift predicted for the system by the AB formalism. Note that the magnetized bar is circled, much like a solenoid, by an A field. The correspondence principle demands that in the classical limit, the effect of A on the electron wavefunction be the same as the deflection of a classical electron beam by the Lorentz force. From the correspondence argument, one might expect that AB phase shifts occur only in situations in which a charged-particle trajectory would be deflected. But the remarkable subtlety and curiosity of the effect is precisely that AB phase shifts occur in cases with no deflection.
Scrutiny and skepsis
Because of its nonobvious nature, the AB effect has endured considerable scrutiny. For example, the effect of stray fields emanating from a finite solenoid was a concern in early attempts to test the effect. 3 Could it be that the stray fields provide a force that makes the effect less purely quantum mechanical?
To visualize where such stray fields can be, consider the experimental scheme illustrated in figure 1 (and see the cover of this issue). An electron wavepacket is coherently split into two wavepackets that pass on opposite sides of the solenoid. Having thus acquired AB phase shifts of opposite sign, the two packets are recombined, and the resulting interference signal depends on the total magnetic flux enclosed by the two paths. It turns out that the measured phase shift agrees well with equation
Another issue that arises with respect to stray fields is the unphysical character of the infinitely long solenoid generally invoked in discussions of the AB effect. So the AB effect has sometimes been dismissed as an extreme limiting case based on an unphysical geometry. A 1986 experiment by a group at Hitachi led by one of us (Tonomura), done with a tiny toroidal magnet, is illuminating in that regard. 4 The magnet’s superconducting niobium cladding excluded any stray fields in that experiment. Its excellent agreement with the AB prediction answers all objections about stray fields and un-physical geometries.
The electron interferogram in figure 3 manifests the AB effect demonstrated in the Hitachi experiment. A coherent electron beam is directed at a microfabricated toroidal magnet. Most of the beam passes by the outside of the magnet, but some of it threads through the magnet’s 4-µm-diameter central hole. A gold outer cladding prevents any electrons from penetrating the magnet itself, and the superconducting inner cladding keeps the hole and the entire vicinity of the magnet free of any stray B fields. But within the magnet’s nonsuperconducting core, where no beam electrons venture, the circling Φ can be varied over several multiples of h/e. Equation

Figure 3. Electron interference pattern demonstrating the magnetic Aharonov–Bohm effect in an experiment that strictly excludes all stray fields.

The electric AB effect
Given the many and varied confirmations of the magnetic AB effect, it is no surprise that textbooks often present the AB effect as a beautiful and closed subject. Nevertheless, an increasing citation rate has pushed the total number of citations of the original AB paper beyond 2500, hardly what one expects for a closed subject with no applications in prospect. The continuing interest is generated, in part, by the fact that two versions of the AB effect were already described in the original 1959 paper: the magnetic version discussed above and the electric version.
If an enclosed magnetic flux can cause phase shifts, one might expect that an enclosed electric flux can do the same. And that is indeed what Aharonov and Bohm predicted. The electric analogue of equation
That’s plausible if one considers that A and V make up a relativistic four-vector just like x and t.
The figure in
There are two versions of the electric AB experiment. In the steady-state version, the electrons do experience fringe electric fields as they enter and exit the tubes. But in the pulsed version, rapid charging and discharging of the tubes is done while the electron wavepackets are fully shielded inside them.
The steady-state version of the experiment was performed in 1985 by Giorgio Matteucci and Giulio Pozzi at the University of Bologna.
5
The small size of electron interferometers prevented the use of actual metallic tubes. Instead, the experimenters ran the electrons past a bimetallic wire charged in such a way as to form a linear dipole field. In that configuration, the nonvanishing electric field produced no deflecting forces. The expected electric AB phase shift from passage on one side of the dipole field had the opposite sign of that on the other side. And that’s what Matteucci and Pozzi found. At the time, their experiment was considered to be a demonstration of what is called a type II Aharonov-Bohm effect. The type I designation is reserved for experiments in which—in principle—the beam particles never traverse an E or B field (see
Insidious mimics
It is now understood, however, that something insidious occurs in the nonpulsed version of the electric AB experiment. Although the electrons are not deflected, they are delayed or sped up by Coulomb forces. When the electrons enter and exit the potentials, those Coulomb forces act in such a way as to mimic the expected phase shift. 6 So the steady-state experiments do not really demonstrate the electric AB effect.
But can the pulsed versions entirely avoid those insidious forces? Perhaps there is also a force description that explains away the magnetic AB effect too. Maybe, pace Einstein, God is malicious as well as subtle. We could ask: Might the electron that passes by the solenoid be inducing changes in the solenoid that act back and impose on the electron a force that mimics the AB prediction?
6
(See
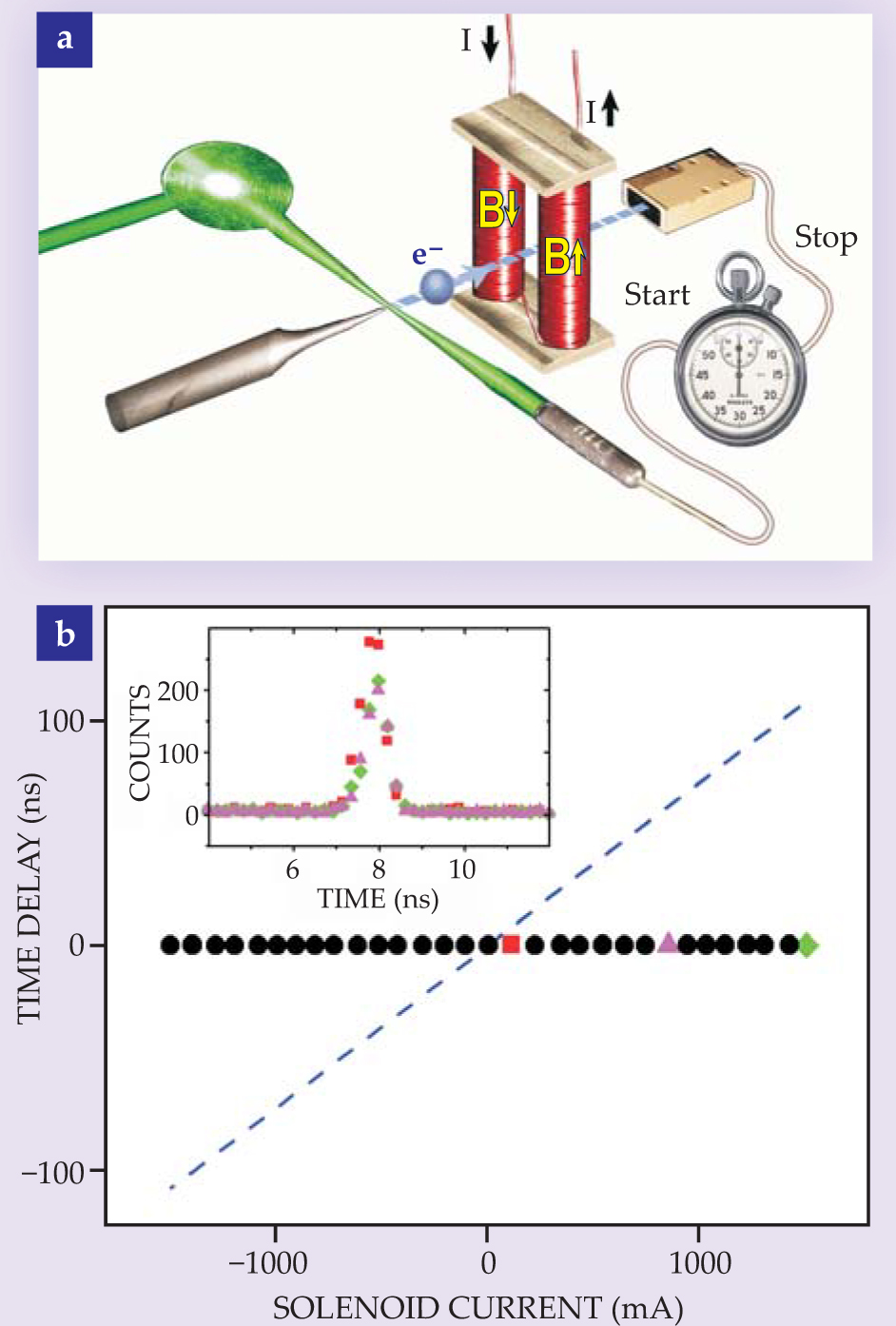
To mimic the magnetic AB phase shift, the solenoid’s reaction force would have to shift the electron wavepacket by a translation Δx = λφAB/2π, where λ is the electron’s de Broglie wavelength. For a wavepacket moving at velocity v, the resulting time delay would be Δx/v. Led by one of us (Batelaan), a group at the University of Nebraska has recently ruled out that reaction-force explanation with an experiment in which electron pulses were shot past solenoids and their arrival times were measured for different solenoid currents (see figure 4). 7 The experiment found no time delays that could mimic the magnetic AB effect.
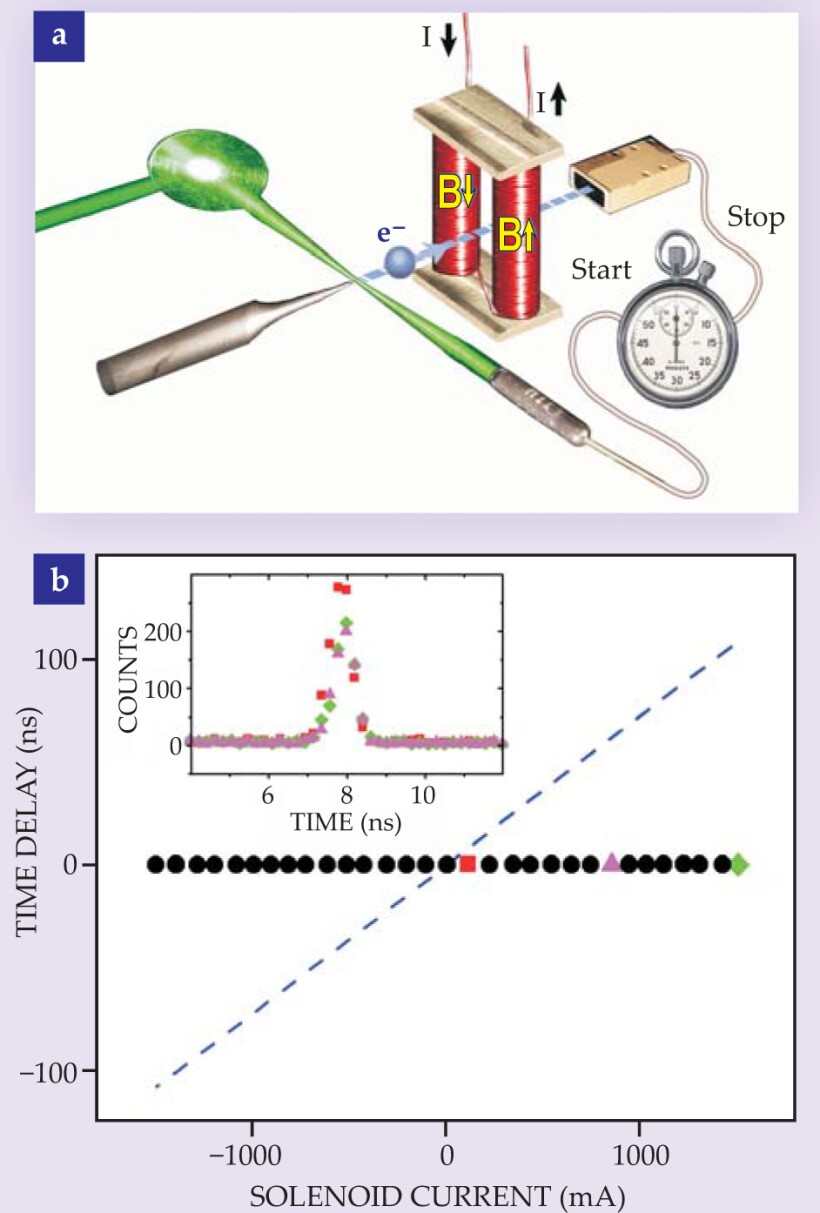
Figure 4. In search of forces that might mimic the magnetic Aharonov-Bohm effect, (a) electrons were sent through a field-free gap between solenoids, and (b) their flight times were measured as a function of the current flowing in opposite senses in the two solenoids. In the absence of current, the flight time between detectors is about 8 ns. If a reaction force from the solenoids is to mimic the AB effect, delays (or advances) relative to 8 ns would have to vary with current like the dashed diagonal line. Instead, the measured time delays are consistent with zero at all currents. The inset shows that the measured spectrum of flight times is essentially the same for low, high, and intermediate currents.
(Adapted from ref. 7.)
A loophole in the interpretation of the Nebraska experiment might be that its solenoids were much bigger than those that demonstrated the magnetic AB effect. 6 Small solenoids might respond differently. It all depends on the interaction time versus the solenoid’s response time. For electron velocities of about 108 m/s and a closest approach of about 10 µm between the electron and a small solenoid, the shortest interaction time would be about 10−13 seconds. For the same beam velocity, a larger solenoid like those in the Nebraska experiment, with diameters on the order of millimeters, has interaction times a hundred times longer.
For comparison, the response time of electrons in a metal is typically 10−14 or 10−13 seconds. Thus the Nebraska delay experiment and the demonstrations of the magnetic AB effect do allow the solenoids enough time to respond, albeit just barely for the small solenoids used in the demonstrations.
Perhaps the ultimate experiment is the one proposed in 1985 by Anton Zeilinger. 8 So far in this discussion, we have only considered what a force does in the classical regime. Zeilinger considered what a force would do in the quantum regime. A large enough solenoid reaction force, he pointed out, would shift wavepackets so much in opposite directions that they would not overlap when recombined. That is to say, if solenoid reaction forces really were mimicking the predicted AB effect, all interference contrast would disappear when the flux in the solenoid was big enough. But if the phase shift really is due to the AB effect, the interference contrast would remain unaffected beyond the length of the wavepacket—or, in a continous electron beam, the beam’s coherence length L c. The coherence length of a continuous beam with a wavelength spread Δλ is given by λ2/Δλ. It’s the separation along the beam beyond which any two points have lost all phase coherence.
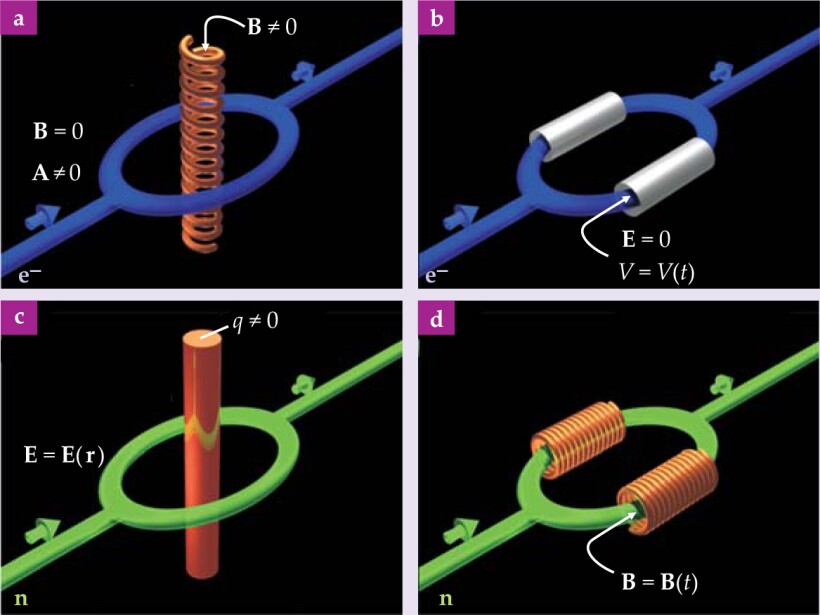
Types and duals
The original magnetic and electric Aharonov-Bohm effects (panels a and b) are type I effects in the sense that in an ideal experiment, the electron sees no B or E fields, though it does traverse different potentials A and V. In their respective dual effects—the Aharonov-Casher effect (panel c) and the so-called neutron-scalar AB effect (panel d)—polarized neutrons (neutral particles with magnetic dipole moments) replace unpolarized electrons, and electrostatic configurations change places with solenoids. 10 In panel c, a neutron interferometer encloses a line of charge, and in panel d, neutrons pass through pulsed solenoids. These duals are classified as type II effects because the neutron must traverse a nonvanishing E or B field.
In either case, to acquire an AB phase shift, the electron or neutron must pass through a region of nonzero electromagnetic potential. That quantum mechanical result seems to elevate the status of the potentials to a physical reality absent from classical electromagnetism. Yakir Aharonov has pointed out that the potentials do overdetermine the experimental outcome; the phase shift need only be known modulo 2π. An alternative view is that the original magnetic AB effect shows electromagnetic fields acting nonlocally. 1
For type II effects, the wavepackets can plow straight through force fields, and forces are allowed in the interaction. But the AB interpretation requires that the emerging wavepackets not be deflected or delayed in any way. Quantum mechanical descriptions generally circumvent the notion of forces. But one can use here an operational definition of forces that might be mimicking an AB effect: If the interaction has produced no deflection or delay, there were no forces.
Dispersion
To visualize the shift of a wavepacket, as distinguished from a quantum phase shift, it is useful to describe what happens to the packet’s frequency components. If each frequency component accumulates the same phase shift after passage by the solenoid—which is what the AB effect predicts—the wavepacket’s envelope function does not shift. That generally accepted view is captured by the concise statement that the AB effect is dispersionless. But if, on the other hand, some back-reaction force were giving different Fourier components different phase shifts that depended linearly on frequency, the wavepacket’s envelope function would indeed shift. (See the interactive Flash movie accompanying the online version of this article.) Experimentally, the observation of electron fringes beyond the beam’s coherence length would verify the AB effect’s dispersionless character.
The extraordinary difficulty of such an experiment becomes clear when one compares the electrons’ de Broglie wavelength to the coherence length, which is also the smallest possible wavepacket length for a given Δλ. In the relevant experimental regime, the typical L c is 105 times λ. A longer λ means unacceptably low electron momentum, and a shorter Lc means an unacceptably large momentum spread. So one would have to observe 105 interference fringes to test for dispersion. Thus far such experiments, crucial as they are to the characterization of the AB effects, have remained out of reach.
Nor has the pulsed version of the original (type I) electric AB effect ever been performed. The development of new pulsed electron sources and detection schemes may change that situation. In 1999 Ahmed Zewail received the Nobel Prize in Chemistry for developing ultrafast sensing techniques (see Physics Today, December 1999, page 19
A paradox
Yakir Aharonov and Daniel Rohrlich have posed a fully classical paradox that they regard as “crucial for clarifying the entirely quantum interactions of fluxons [flux quanta] and charges—the generalized Aharonov–Bohm effect.”
17
The paradox involves the interaction of a charge with a magnetic flux tube, just as in the original magnetic AB effect. The magnetic flux tube is realized with symmetric charge and current distributions (see the
Outside the tubes there is no electric or magnetic field (the latter assuming the tubes are very long). So a charged particle at rest outside the tubes should stay where it is. But if friction between the tubes causes their spins to decelerate, something curious occurs. Faraday’s law dictates that the diminishing magnetic flux inside the tubes induces an electric field outside. The electron experiences a force F and accelerates, but the tubes do not. What happened to momentum conservation?

Aharonov and Rohrlich reply that one must take account of momentum in the electromagnetic field and “hidden” relativistic mechanical momentum in the tubes. Many paradoxes are based on field momentum, and hidden momentum is a difficult concept that has been debated for decades. With regard to the AB effect, identifying all the (relativistic) classical momentum terms and all the forces associated with the interaction between flux quanta and charges is not easy. 18 So experiments have an important role to play.
Duals
Are the original magnetic and electric AB effects isolated phenomena? If they really exist, should they not be mirrored in other physical systems? Aharonov’s answer is affirmative. In a 1984 paper, he and Aaron Casher predicted that both the magnetic and electric AB effects have their so-called duals, in which electric charges and magnetic dipoles exchange roles (see
A series of experiments have confirmed those ideas. 10 For example, in a tour de force 1992 experiment at the University of Melbourne, Brendan Allman and coworkers demonstrated the dual of the electric AB effect by passing longitudinally polarized neutrons through pulsed solenoids. They did find a phase shift that agreed with the prediction. But that dual is intrinsically a type II effect, because the neutrons must pass through a nonvanishing B field. Their polarization parallel to the solenoid field is meant to eliminate Lorentz forces. Nonetheless, the Melbourne group’s interpretation was alternately disputed and supported by dueling theorists. The controversy was eventually resolved by a follow-up experiment that observed the phase shift beyond the neutron beam’s coherence length, yielding a rare demonstration of the dispersionless character of an AB phenomenon. 11
The dual of the magnetic AB effect is also a type II effect, in that the neutrons traverse regions of nonvanishing electric field. It was experimentally realized by enclosing charged, straight electrodes within the two arms of a neutron interfe-rometer. 12 It is interesting to compare that physical scenario with the Mott–Schwinger effect, in which neutron scattering off nuclei is attributed to the force between the nuclear charge and the incident neutron’s magnetic dipole. 13 On the other hand, the interactions of neutrons with line charges is considered to be a true AB effect. As far as we know, there hasn’t been a unified theoretical or experimental treatment of the two effects. With increasingly refined neutron sources becoming available, it may soon be possible to distinguish experimentally between the force-driven scattering of neutrons off a charged sphere and the presumed absence of such a force in their interaction with a charged line.
Still more AB phenomena
Although solid-state manifestations of the AB effect are not the main topic of this article, we would hardly do justice to the breadth of the effect without mentioning them and the experimental breakthroughs that have made them possible. The first step was the 1985 observation, by Richard Webb and coworkers at IBM, of the AB effect for electrons circulating in a mesoscopic ring of nonsuperconducting metal
14
(see Physics Today, January 1986, page 17
Not having to rely on superconductivity in the creation of a solid-state electron interferometer lets the experimenter avoid the complication of flux quantization, and it permits the investigation of new quantum effects in disordered materials. More recently, the observation of electron interference in carbon nanotubes suggests that the microscopic regime is also accessible for AB investigations. 15
In all the solid-state experiments, mesoscopic and microscopic, the AB phase shift was observed even though magnetic fields were present throughout the interferometer. That makes them a bit different from the enclosed-flux experiments with electron beams in vacuum. An important promise that those small solid-state electronic devices offer is their possible application in such areas as quantum computing.
Our discussion thus far has been based on interference between quantum mechanical amplitudes for alternative paths of a single particle. The physics of two-electron interference phenomena has to deal with the additional issue of Fermi–Dirac quantum statistics. A number of two-electron interference experiments in recent years have reported observing the predicted statistical phenomena of antibunching and Hanbury Brown–Twiss interference.
16
(For background on HBT interference, see Physics Today, August 2008, page 8
Nowadays electrons can be used to demonstrate in the laboratory all the elements at the heart of quantum mechanics: wave–particle duality, quantum statistics, nonlocality, and entanglement. Because those elements are important to the prospects for quantum cryptography, quantum teleportation, and quantum computation, a new era of quantum electronics may be at hand.
Aharonov stresses that the arguments that led to the prediction of the various electromagnetic AB effects apply equally well to any other gauge-invariant quantum theory. In the standard model of particle physics, the strong and weak nuclear interactions are also described by gauge-invariant theories. So one may expect that particle-physics experimenters will be looking for new AB effects in new domains.
We thank Adam Caprez for the artwork. This article is based on work supported by the NSF under grant no. 0653182.
References
1. Y. Aharonov D. Bohm, Phys. Rev. 115, 485 (1959). https://doi.org/10.1103/PhysRev.115.485
2. R. G. Chambers, Phys. Rev. Lett. 5, 3 (1960); https://doi.org/10.1103/PhysRevLett.5.3
G. Möllenstedt W. Bayh, Naturwissenschaften 49, 81 (1962).3. A. Tonomura, Electron Holography, 2nd ed., Springer, New York (1999), pp. xi,162;
The Quantum World Unveiled by Electron Waves, World Scientific, Hackensack, NJ (1998).4. A. Tonomura et al., Phys. Rev. Lett. 56, 792 (1986). https://doi.org/10.1103/PhysRevLett.56.792
5. G. Matteucci G. Pozzi, Phys. Rev. Lett. 54, 2469 (1985). https://doi.org/10.1103/PhysRevLett.54.2469
6. T. H. Boyer, Found. Phys. 32, 41 (2002). https://doi.org/10.1023/A:1013896713708
7. A. Caprez, B. Barwick, H. Batelaan, Phys. Rev. Lett. 99, 210401 (2007). https://doi.org/10.1103/PhysRevLett.99.210401
8. A. Zeilinger, in Fundamental Aspects of Quantum Theory, V. Gorini, A. Figerio, eds., Plenum, New York (1985).
9. P. Hommelhoff et al., Phys. Rev. Lett. 96, 077401 (2006). https://doi.org/10.1103/PhysRevLett.96.077401
10. Y. Aharonov A. Casher, Phys. Rev. Lett. 53, 319 (1984); https://doi.org/10.1103/PhysRevLett.53.319
B. E. Allman et al., Phys. Rev. Lett. 68, 2409 (1992); https://doi.org/10.1103/PhysRevLett.68.2409
G. Badurek et al., Phys. Rev. Lett. 71, 307 (1993); https://doi.org/10.1103/PhysRevLett.71.307
W.-T. Lee et al., Phys. Rev. Lett. 80, 3165 (1998). https://doi.org/10.1103/PhysRevLett.80.316511. G. Badurek et al., Phys. Rev. Lett. 71, 307 (1993). https://doi.org/10.1103/PhysRevLett.71.307
12. A. Cimmino et al., Phys. Rev. Lett. 63, 380 (1989). https://doi.org/10.1103/PhysRevLett.63.380
13. J. Schwinger, Phys. Rev. 73, 407 (1948). https://doi.org/10.1103/PhysRev.73.407
14. R. A. Webb et al., Phys. Rev. Lett. 54, 2696 (1985). https://doi.org/10.1103/PhysRevLett.54.2696
15. A. Bachtold et al., Nature 397, 673 (1999); https://doi.org/10.1038/17755
J. Cao et al., Phys. Rev. Lett. 93, 216803 (2004). https://doi.org/10.1103/PhysRevLett.93.21680316. M. Henny et al., Science 284, 296 (1999); https://doi.org/10.1126/science.284.5412.296
W. D. Oliver et al., Science 284, 299 (1999); https://doi.org/10.1126/science.284.5412.299
H. Kiesel, A. Renz, F. Hasselbach, Nature 418, 392 (2002); https://doi.org/10.1038/nature00911
I. Neder et al., Nature 448, 333 (2007). https://doi.org/10.1038/nature0595517. Y. Aharonov, D. Rohrlich, Quantum Paradoxes: Quantum Theory for the Perplexed, Wiley–VCH, Weinheim, Germany (2005), p. 177.
18. W. Shockley R. P. James, Phys. Rev. Lett. 18, 876 (1967); https://doi.org/10.1103/PhysRevLett.18.876
H. A. Haus P. Penfield Jr, Phys. Lett. A 26, 412 (1968); https://doi.org/10.1016/0375-9601(68)90249-1
W. H. Furry, Am. J. Phys. 37, 621 (1969); https://doi.org/10.1119/1.1975729
L. Vaidman, Am. J. Phys. 58, 978 (1990); https://doi.org/10.1119/1.16260
T. H. Boyer, J. Phys. A 39, 3455 (2006). https://doi.org/10.1088/0305-4470/39/13/021
More about the authors
Herman Batelaan is a professor of physics at the University of Nebraska-Lincoln. Akira Tonomura is a fellow at Hitachi Ltd and a group director at the RIKEN Frontier Research System in Saitama, Japan. He is also a principal investigator at the Okinawa Institute of Science and Technology.
Herman Batelaan, 1 University of Nebraska–Lincoln .
Akira Tonomura, 2 Okinawa Institute of Science and Technology .




