Crystal growth in ice and snow

Ice shapes our world. The water-to-ice phase transition tempers the climate, fractures rock, and squeezes material caught in interstitial ice grain boundaries. The vapor-to-ice transition produces symmetric snowflakes that are both beautiful and fascinating. These phenomena and more have their roots in the building blocks—made from water molecules—that compose ice and snow.

More than 400 years ago, well before scientists knew about molecules, Johannes Kepler pondered the relationship between building-block packing and the hexagonal shape of snowflakes. ¹ We now know that the core of a snowflake consists of a single crystal of so-called hexagonal ice, I_h, the first elaborated of 17 known phases of ice. The lacy structure of snowflakes builds on that single-crystal core as additional vapor molecules condense on the surface. The growth of single-crystal ice from liquid water also proceeds from sequential condensation events, but in ways significantly different from snowflake growth.

The internal structure of ice has been known since the advent of x rays. But the surface binding that grows ice and snowflakes is different from binding in the bulk. In due course, I’ll present a molecular-level model that elucidates the surface growth process. The laboratory environment in which researchers grow single-crystal ice is quite different from the clouds in which vapor condenses into snowflakes, and I’ll also discuss how the different environments affect the growth process. But first, I invite you to join me on a visual tour of snowflake structure at multiple scales—from the macroscopic hexagonal prism that is the core of all the observed shapes, to the microscopic surface structures revealed by etching single crystals, to the molecular-level surface configuration detected by atomic scattering.

Symmetry within chaos

Snowflake growth starts with a surface on which water vapor can condense. In the environment, seeds are provided by many kinds of particulate matter, including pollen, mineral dust, and salts created when ammonia neutralizes acidic gases in the atmosphere. Exactly how the nascent snowflake forms on the solid seed remains uncertain, as demonstrated by the still not quite successful efforts to seed clouds. ² Nonetheless, if conditions are right, a perfect hexagonal ice crystal nucleates on the seed and the nascent flake grows. ³ Usually the mature flake has six elaborate and nearly identical sides, but as figure 1 shows, nature can display other forms.

Figure 1.

The symmetry and variety of snowflakes have fascinated scientists and nonscientists alike. How can molecular forces that act on the subnanometer-to-nanometer scale operate so that parts of the crystal literally billions of molecules away assemble in the same way, yet any two snowflakes are highly unlikely to be identical? The first steps toward answering the question came in the 1930s, when Ukichiro Nakaya diagrammatically cataloged the importance of temperature and relative humidity on crystal morphology. ⁴ In brief, he found that thin plates form at −2 °C, long needles at −5 °C, thin plates again at −15 °C, and thick plates and columns at −25 °C. He also observed that at low relative humidity, the crystals grow slowly and develop few branches. Conversely, high relative humidity supports more rapid growth and more abundant branches.

Although the relative humidity and temperature vary from location to location in a cloud, on the tiny scale of a snowflake they are constant. As a result, snowflake growth is essentially perfectly symmetric. On the other hand, as tiny snowflakes blow around in the chaos of the cloud, buffeted by the wind and perhaps warmed by the Sun, individual flakes are highly unlikely to experience exactly the same set of varying conditions. As a result, pretty much every snowflake is unique.

Nakaya’s morphology diagram is observational. It does not explain why the structure changes with temperature from plates to needles to columns or why high relative humidity supports dendritic growth. Ultimately, the answers lie in energy and kinetics considerations at the nanoscale. Before arriving at the nanoscale, however, we will take a detour to the microscopic level to see the context in which the nanoscale physics operates.

Etch pits

The heart of every snowflake is a single, hexagonal prism ice crystal. Figure 2a shows the geometry and identifies three distinct types of crystal face: the hexagonal basal faces that cap the prism, the rectangular primary faces on the sides, and the secondary faces formed by cleaving along the line connecting alternate hexagon points. Snowflake cores are micron sized, delicate, and ephemeral, but to get at their microscopic structure, it is not necessary to deal with such fragile systems. Instead, one can explore etch pits created by the sublimation of material from the surface of a larger, single crystal.

Figure 2.

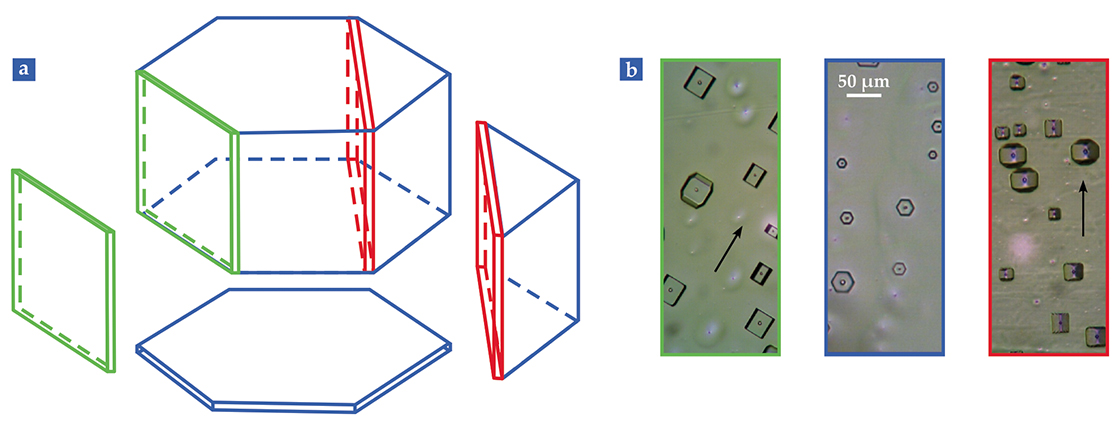
First, cleave a flat surface on the crystal and coat it with a thin polymer film that naturally forms with minute pinholes. Water molecules sublimate through the pinholes. Etching is thus the reverse of the process by which snowflake cores develop by condensing vapor-phase water molecules onto the growing surface. Suppose, for example, that the crystal is cleaved along a basal face. Then the etch pits will be tiny hexagons, just like the cores of snowflakes. The etch pits that arise if the crystal is cleaved along a primary or secondary face are perhaps harder to visualize, but they are shown in figure 2b, along with the basal hexagons. For me, the etch pits illustrate one of the satisfying aspects of ice research: the visual connection between macroscopic and microscopic structure.

The basal, primary, and secondary faces are the major characters in the story of growing ice. Usually, lacy snowflake structures originate at the hexagonal prism points. Thus the advancing ends are secondary prism faces. When single-crystal ice is produced in the lab, the secondary prism face is again most likely to propagate. To understand why requires an exploration of ice at the molecular scale, the next step in our tour.

A hidden hexagon

Consideration of the molecular-level ice structure raises a question, only recently answered, that is directly relevant to face stability and growth out of the hexagonal corners. ^{5 , 6} The question may be stated with the help of figure 3a, which shows two distinct hexagonal structures in the ice basal face. The first hexagon structure (red and white in the figure) is familiar to students of chemistry and molecular physics. The second (blue) is larger, is rotated by 30° with respect to the other hexagons, and consists of six water molecules surrounding a central water molecule. Which hexagon structure coincides with the snowflake core?

Figure 3.

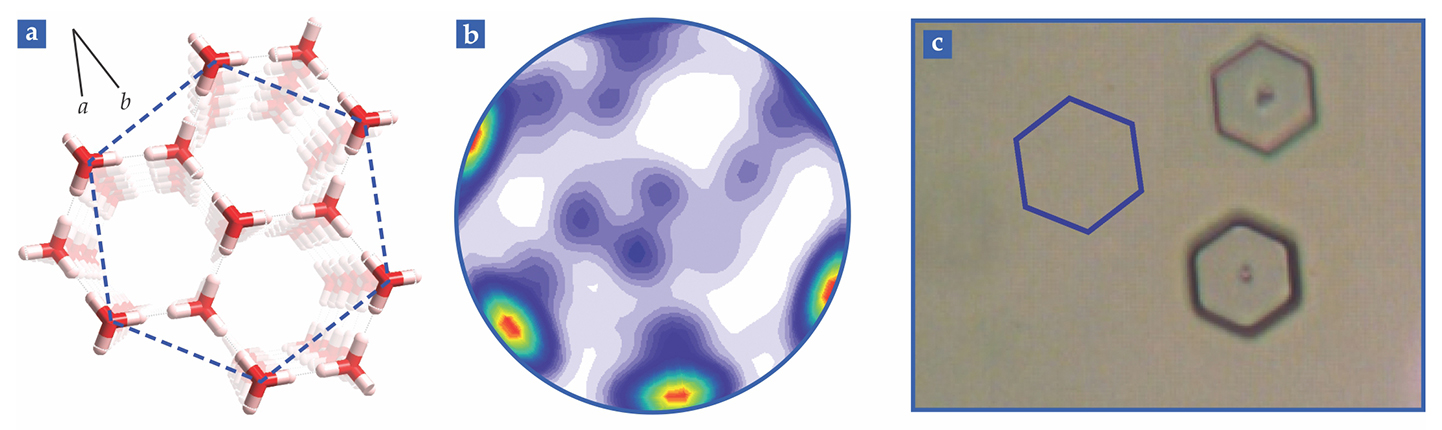
Last year my colleagues and I reported an answer to the question. ⁶ Part of the reason it took so long is that substrate preparation is difficult. Crystal impurities and stresses found in the environmental ice used in previous work muddied the data interpretation, but the advent of laboratory methods for growing large, optically perfect single crystals ⁷ enabled us to clear away the mud. Our approach was to carefully ensure the same sample orientation for etching and for probing with electron backscatter diffraction and then to correlate the resulting etch pits and orientation density functions (see the box). By doing so, we could establish that the hexagonal prism at the core of a snowflake corresponded to the larger of the microscopic hexagons in figure 3a. Figures 3b and 3c show some of our results.

A more detailed look at snowflakes at the molecular level illuminates why dendrites typically grow out of the hexagonal points. Specifically, I will examine the molecular structure of the primary and secondary prism faces. A primary face, we now know, corresponds to a flat side of the blue dashed hexagon in figure 3a. As figure 4 shows, the face’s top layer consists of pairs of water molecules in a row structure. A secondary prism face corresponds to a flat side of the red-and-white hexagon in figure 3a. Its top layer has chains of water molecules. To successfully dock onto the growing surface, the incoming water molecule must orient to complement the existing surface. That is, a covalently bonded hydrogen atom of the incoming molecule must link with an open valence (unshared electron pair) of a surface oxygen atom. Conversely, an open valence on the incoming molecule must link with an O–H group dangling from the surface.

Figure 4.

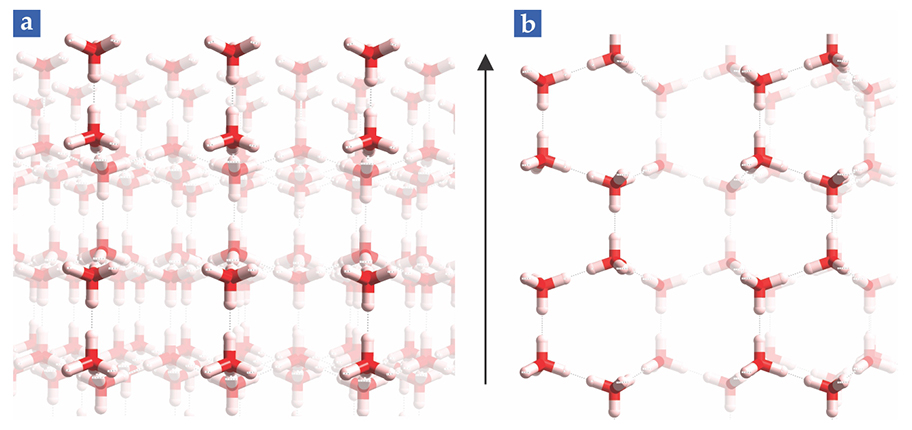
The pair configuration of the primary face affords greater flexibility in forming a successful dock than does the chain configuration of the secondary face. More precisely, the surface entropy is greater for the primary face. But entropy is just one component of a surface’s free energy. The other is enthalpy—the heat of fusion released when vapor condenses to grow the snowflake. Enthalpy favors docking at the secondary prism face, which has a greater valence density. Most of the time, snowflakes grow by advancing the secondary prism face.

However, the free energies of the three major prism faces are nearly the same, and small temperature and humidity variations in a cloud encourage different kinds of growth. Each snowflake experiences a unique history, and thus each snowflake is unique.

Having completed our multiscale tour and looked at some of the thermodynamics of ice, let us review some of the varied snowflake forms shown in figure 1. In the humid conditions that favor highly branched structures, the secondary prism face gathers water molecules rapidly and grows branches. Released heat of fusion maintains the high humidity in a positive feedback loop. The growth is actually so rapid that the branches develop imperfections that send them in a new direction oriented 60° away, in accord with the ice crystal’s hexagonal symmetry. The result is beautiful dendrites, as depicted in figure 1a.

The existence of 12-sided snowflakes, as in figure 1b, indicates that if the temperature and humidity are right, the primary prism face can ably compete with the secondary face to grow dendrites. Again, a positive feedback loop maintains growth.

Ridged snowflakes, as in figure 1c, form in calm conditions with constant temperature and relatively low humidity. In such an environment, domains sprouting from adjacent hexagonal points grow large enough to fill in the space between them. Crystal imperfections resist the smooth joining of adjacent domains. Water molecules bridge the domains, but stress from the bridging creates ridges at the domain junctions.

Columnar snowflake crystals, as in figure 1d, start life in a cold, low-humidity environment that favors growth of the primary prism face. As the snow crystal grows, it is blown to a region of the cloud with more typical conditions, and there it becomes capped with a large basal face. Nakaya’s morphology diagram shows that the temperature variation between growing a long ice crystal and capping the ends with plates can be as little as 3 °C. Those little barbell-shaped snowflakes are excellent thermometers.

Laboratory-grown ice

Our experiments to answer the hexagon riddle of ice structure were possible only because we could grow single-crystal ice in the laboratory. Fabricating such a crystal might seem to be a trivial task; just put some water in the freezer. Alas, water contains dissolved gases, which is why ice cubes typically have bubbles in them. Furthermore, ice cubes consist of thousands of small crystallites. Another approach is needed to grow a single crystal.

At the macroscopic stop of the multiscale tour, I noted that snowflakes require a seed to initiate growth. That is because clean water supercools—remains liquid—to temperatures as low as −46 °C. So, like snowflakes, laboratory-grown ice requires a seed. Once nucleated, water and other supercooled materials solidify rapidly and generate many crystal domains.

To make single-crystal ice, we started with a polycrystalline seed, grew at 0 °C, and took advantage of competitive growth to winnow down to just one domain. Winnowing begins with a short capillary that connects the seed bulb to a growth tube. As the frozen front advances through the capillary toward the growth tube, the lowest-free-energy, most stable face occupies a larger and larger fraction of the liquid–solid interface. A length of 5 millimeters accommodates a million layers—a million generations—which is ample opportunity for survival of the stablest. Then a flared-out crucible region of the growth tube magnifies the one to five domains that typically survive the capillary stage. Final selection occurs as the crucible constricts to a narrow neck and spatially filters out one domain that seeds the main body. Voilà, a single crystal.

Because the ice sample takes on the shape of its container, it does not reveal the orientation of the ice lattice; etch pits do. If the surface of the single-crystal happened to be precisely aligned along a basal, primary, or secondary face, the etch pit would look like one of the examples in figure 2. In general, such a fortuitous orientation is not the case, and determining the actual orientation is an exercise in three-dimensional geometry.

Imagine a virtual hexagonal prism partially embedded in the surface, as shown in figure 5. Removing the prism leaves a pit whose profile reveals the orientation of the original prism. To specify the orientation, first consider the so-called tilt angle θ between the axis of the growth tube, or boule, and the axis of the hexagonal prism. In the figure, the tilt angle is about 80°, which is a typical result. Indeed, the most likely tilt angles are in the range of 70°–90°, and tilt angles less than 45° are never observed. The boule cross section is a frozen record of the growth front. Given that the tilt angle is not zero, the basal face is not that front. It is, in fact, the least stable of the three major ice faces. If snow ice grew from the liquid rather than from the vapor, snowflakes would all be columnar.

Figure 5.

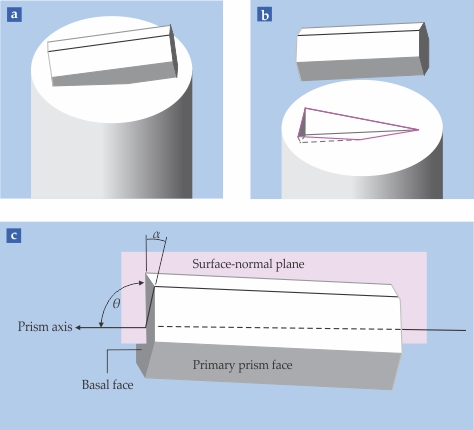
Rotation about the prism axis is called the roll angle α. It is measured from a hexagonal point to the surface-normal plane, which is determined by the boule and prism axes. For example, if the point faces directly into the boule, the roll angle is 0° and the growth front is a secondary prism face. A roll angle of ±30° indicates that the primary prism face is the growth interface. In observations of growth in hundreds of boules, about 60% of the growth fronts have roll angles near 0°, 30% have angles near ±30°, and 10% are between those extremes.

The near-equilibrium growth of single-crystal ice in boules favors the secondary prism face, though the primary face offers reasonable competition. The secondary prism face is thus the most stable face for the liquid–solid interface. The results are not surprising in light of the entropy and enthalpy of the faces’ molecular structures. Entropy favors the primary face over the secondary one, and both of those are favored over the basal face. The secondary prism face has a slight enthalpy edge over the primary prism face, and both have an advantage over the basal face. At the 0 °C temperature of the growth front, enthalpy slightly edges out entropy.

In retrospect, the development of the snowflake seems odd. If the secondary prism face has the lowest free energy and indeed is often the advancing front, why is the area of a snowflake dominated by the basal face, with the secondary face occupying only a small fraction of the area? One key is heat conduction. For ice grown in liquid, the growth front has good thermal contact with the ice and water baths on either side of it. The baths easily conduct away heat of fusion provided the growth is slow enough. In snow clouds, one side of the growth front is vapor, a poor heat conductor, and the other is a thin dendrite, which is hardly a heat sink. As a result of inefficient heat conduction and high heats of fusion, the primary and secondary fronts vaporize and the basal face of the snowflake has a relatively large area. Topology may also be important. The surface of a snowflake is a closed 2D area in 3D space. In contrast, the liquid–ice system is enclosed in a boule; the growth face is planar. I also note that the theoretical modeling of ice and water is quite challenging, in part because of the quantum nature of the proton.

Box. The orientation density function

Quantum mechanics teaches us that electrons are waves, so electrons scattering from crystal planes produce constructive and destructive interference if the electron wavelength is comparable to the crystal lattice spacing. The scattering pattern can be interpreted to find the normals to the scattering planes. Three normals are relevant; they are called a (red), b (green), and c (blue) crystallographic axes. The c-axis is perpendicular to the basal plane of a snow crystal. Crystallographic a- and b-axes are defined in figure 3a; a priori one doesn’t know which of those two axes is directed toward the hexagonal points of an actual snow-crystal core. But—spoiler alert—the illustration shows the proper correspondence.

In our work, we present the scattering information as a two-dimensional figure called an orientation density function (ODF). Imagine that the sample is enclosed in a sphere. At least some of the outward-directed normals intersect the northern hemisphere; the figure shows one example for each crystallographic axis. Connect the intersection points to the south pole and mark where the connecting line crosses the equatorial plane. Repeat the procedure over hundreds of scattering events, express the likelihood that a given equatorial point is crossed, and you’ve got an ODF.

A tight clustering of equatorial crossings indicates a single crystal, and the specific crossing spots indicate how the crystal is oriented. For example, if the basal plane is parallel to the projection plane, the ODF associated with the a-axes would display six equatorial crossings that correspond to the directions of the six vertices of the blue hexagon shown in figure 3a. (In this idealized special case, the northern hemisphere intersections would correspond to the equatorial crossings.) Indeed, figure 3b shows an ODF for a crystal with almost that perfectly basal orientation.

Tools of the trade

Particularly in the atmosphere, ice likely shapes the world in ways that are not yet appreciated but that are amenable to explorations with the tools now available to researchers. Single-crystal ice samples can be grown in the laboratory in a reasonable time. Etching serves to determine crystal lattice orientation, and by cutting the sample appropriately, investigators can generate whatever faces they want to look at.

Nearly any molecular-level question of interest is still open. Secondary prism face chains have been detected spectroscopically, ⁸ but the primary face pairs have not been probed. Chemistry on either of the two faces is yet to be explored. Dangling valences on the ideal prism faces seem to be oriented in a manner nearly perfect for small-molecule docking, a phenomenon that could have a profound effect on the environment. The future looks bright for ice researchers, who can look forward to learning much more about one of our most common and fascinating materials.