Synthetic dimensions
DOI: 10.1063/PT.3.5225
Objects move through three dimensions in space. But a wide range of experiments that manipulate atoms, molecules, and light can engineer artificial matter in ways that break even that basic law of nature. Such matter can behave as if it were extended to four or more spatial dimensions or restricted to just one or two, as determined by experimental design.
The techniques used by those experiments can control not only dimensionality but also spatial geometries and potential-energy landscapes. Even in one dimension, these abilities have made synthetic dimensions an exciting method to explore topological physics, where precise control of the landscapes is necessary. Frequently, synthetic dimensions are created in ultrasmall and ultracold systems, where the experiments provide powerful access to the hard-to-understand world of interacting quantum matter, which underpins fields as diverse as quantum gravity and solid-state physics.
To understand synthetic dimensions, it helps to distill physical theories into two basic ingredients—the set of states a system can occupy and the rules describing how to move between them. In classical mechanics, for instance, a state is composed of the positions and velocities of particles, and the rules are Newton’s laws. Dimensionality is defined by those rules. Particles in one-dimensional systems can step only forward or backward, much like a tightrope walker. In three dimensions, they can also move up or down and right or left.
Synthetic dimensions refer to the degrees of freedom belonging to a single particle controlled in a particular way. The idea is simply to allow some set of states to play the role of spatial positions and then to apply controls—usually electromagnetic fields—that implement the desired rules of motion. That protocol creates a system that is mathematically equivalent to a particle moving in a new spatial dimension. And it provides novel capabilities for controlling geometry and motion.
Rydberg atoms
In this Quick Study, we focus on synthetic dimensions made with highly excited atoms, known as Rydberg atoms. Synthetic positions are created from the atoms’ excited electronic states, while microwave-frequency radiation drives transitions between those states and dictates the rules for what motions are allowed. Those rules are mathematically equivalent to those obeyed by particles in a real lattice—for example, electrons moving in a crystal or molecule.
Figure
Figure 1.

Rydberg atoms as quantum simulators. Highly excited electronic states of strontium-84 atoms (left) that are cooled to nanokelvin temperatures act as position states r, and microwave fields drive transitions between them. States of the Rydberg atoms are connected in a one-dimensional geometry, and a staggered pattern of different tunneling strengths J mimics the lattice structure found in the organic conductor polyacetylene (right). Dynamics in the synthetic dimension are mathematically equivalent to the electron moving between atomic sites in a real molecule.
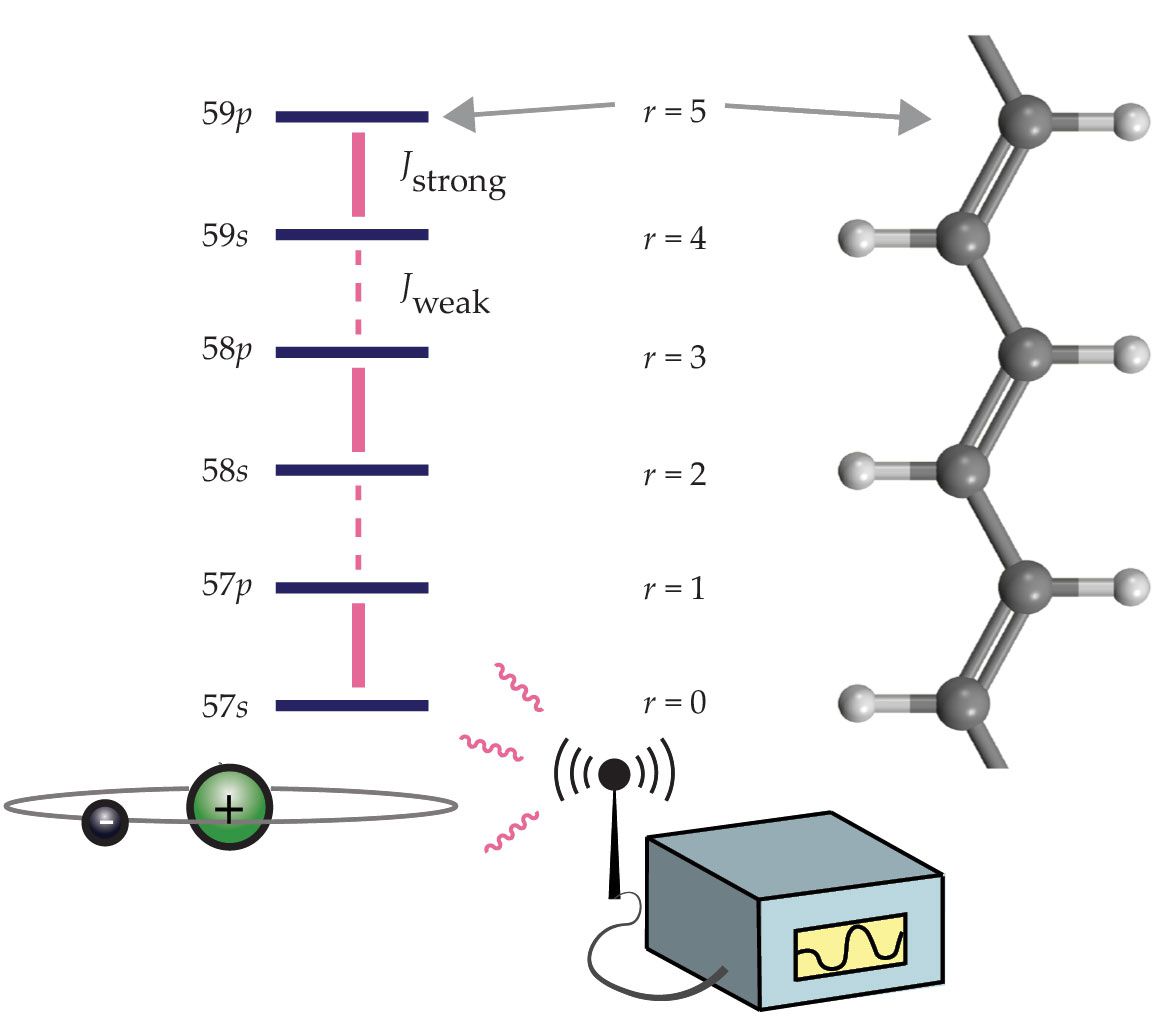
In polyacetylene, electrons move between adjacent carbon atoms by quantum mechanical tunneling. The rates of that motion are slower (Jweak) or faster (Jstrong), depending on whether the atoms are single or double bonded. (A so-called Peierls instability, or distortion, leads to the two distinct alternate bonding configurations in polyacetylene.) The equivalent processes in the synthetic dimension are created by microwave radiation driving transitions between adjacent Rydberg states. Importantly, because pairs of electronic levels are separated by different resonance frequencies, each tunneling rate can be controlled independently. The full lattice structure is formed by many transitions being driven at the same time.
The polyacetylene-inspired model, known as the Su-Schrieffer-Heeger model, harbors spatially localized states known as topological edge states at the boundaries of the molecule’s chain. The presence of those states is not itself an exotic effect. Their energies, however, are robust to all local perturbations obeying a special symmetry of the model. And that protection against noise and disorder has made topology of great interest to condensed matter, materials science, and quantum information.
The suitability of the synthetic-dimensions approach to topological physics stems from its unique ability to create the precise configurations of tunneling elements necessary to realize topological lattice models and potential-energy landscapes. The general ease of performing state-resolved detection also allows for direct access to site-resolved measurements in the synthetic dimension. (See the article by Victor Galitski, Gediminas Juzeliūnas, and Ian Spielman, Physics Today, January 2019, page 38
In the study by Killian and Dunning, those ingredients were combined to engineer protected boundary states and to directly image them through what one might call a single-site-resolved synthetic microscope. More generally, synthetic dimensions are appealing in being able to produce intricate tunneling arrangements and in allowing measurements of the populations of each site, potentially as a function of time.
The future of dimensions
The synthetic-dimensions concept is quite broad and has been implemented in ground-state atoms, Rydberg atoms, molecules, and a variety of architectures using light. While internal states often serve as the synthetic positions, as we described earlier, experimentalists can also use motional states, such as the quantized energy levels of an atom in a box, as synthetic states as well. In that case, transitions involve moving a whole atom between the eigenstates of an external potential—in contrast to electronic transitions driven between states of an atomic potential. Both electronic- and motional-state approaches are conceptually similar but differ in the length, energy, and time scales that each involves.
Some of the most notable achievements of synthetic dimensions include the direct study of protected edge states in topological models for neutral atoms and photons. Indeed, the capabilities to create rich tunneling arrangements and sharp edges follow naturally from the way that motion is induced through electromagnetic fields. Beyond those common capabilities, synthetic-dimension platforms have complementary strengths and limitations. Photons can access a nearly arbitrary number of states in, for example, a synthetic dimension formed by the frequency of light. But photons rarely interact strongly with each other. Rydberg atoms, by contrast, can strongly interact but are difficult to handle when coupling many states.
We expect the research field to grow, with improved coherence, larger numbers of states, and new capabilities for control. Improvements in the control of many different transitions, in particular, would allow researchers to explore more exotic phenomena—including geometries that are physically challenging to create in nature (see figure
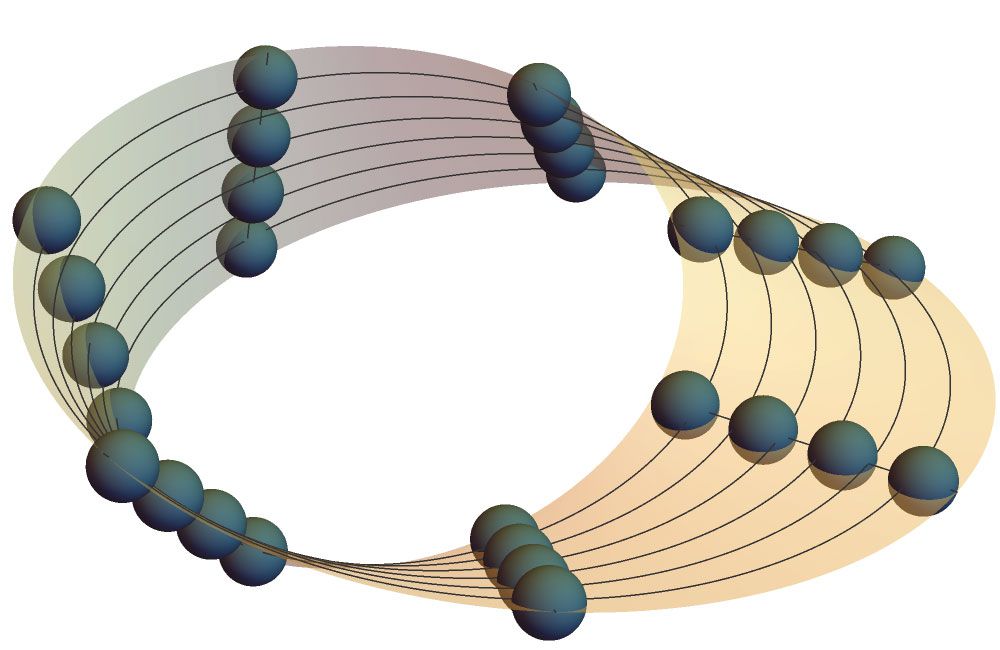
Figure 2.
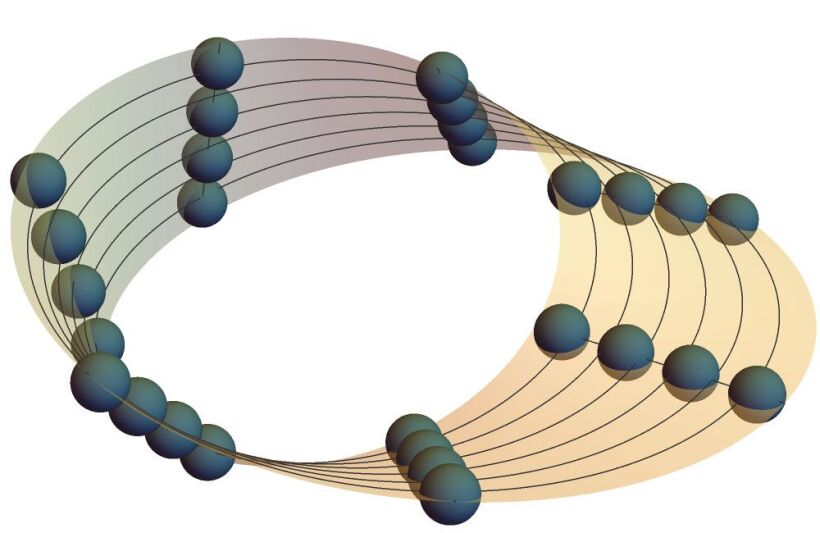
Möbius maneuvers. Synthetic dimensions give experimentalists the tools to reproduce geometries that are difficult or impossible to create in real space. The famous Möbius-strip geometry, for instance, can be created by connecting the Rydberg energy levels (balls) with microwave-driven transitions (lines). The proper geometry emerges when one chooses an appropriate set of Rydberg levels and then drives transitions between them. Along the strip’s width are transitions that change the angular momentum ℓ but keep the principal quantum number n fixed; and along its circumference are transitions that change both ℓ and n.
To date, most experiments have concentrated on single-particle physics and (nearly) noninteracting particles. But the deepest mysteries about quantum matter occur for systems of interacting particles, where new and poorly understood phases of matter can emerge. Those systems are generally difficult to computationally simulate. And the cost of simulating even simple models grows exponentially with the number of particles. Fortunately, synthetic dimensions can serve as an effective quantum simulator. One may engineer designer systems governed by the same physics as the system of interest—be it electrons in a material or quantum matter near a black hole—and explore its physics in a synthetic-dimensions experiment.
References
► T. Ozawa, H. M. Price, “Topological quantum matter in synthetic dimensions,” Nat. Rev. Phys. 1, 349 (2019). https://doi.org/10.1038/s42254-019-0045-3
► L. Yuan et al., “Synthetic dimension in photonics,” Optica 5, 1396 (2018). https://doi.org/10.1364/OPTICA.5.001396
► O. Boada et al., “Quantum simulation of an extra dimension,” Phys. Rev. Lett. 108, 133001 (2012). https://doi.org/10.1103/PhysRevLett.108.133001
► A. Celi et al., “Synthetic gauge fields in synthetic dimensions,” Phys. Rev. Lett. 112, 043001 (2014). https://doi.org/10.1103/PhysRevLett.112.043001
► S. K. Kanungo et al., “Realizing topological edge states with Rydberg-atom synthetic dimensions,” Nat. Commun. 13, 972 (2022). https://doi.org/10.1038/s41467-022-28550-y
More about the authors
Kaden Hazzard (kaden.hazzard@gmail.com) is a theoretical physicist and associate professor at Rice University. Bryce Gadway (bgadway@illinois.edu) is an experimental physicist and associate professor at the University of Illinois at Urbana-Champaign.






