What’s inside a crumpled ball?

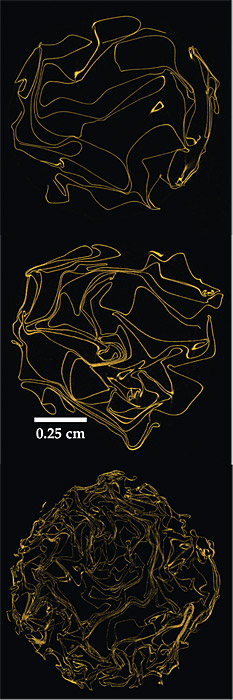
A worm inside a head of cabbage can learn a lot by looking around. From the curvature of the surrounding leaves, it can get a good sense of how far it is from the center of the cabbage, and from the leaves’ orientation, it can figure out which direction provides the shortest route to the surface. A worm within a crumpled ball of paper is not so lucky: No simple local measurement of the surrounding layers points the way out of the ball or suggests how far the journey might be. That’s what Dominique Cambou and Narayanan Menon, of the University of Massachusetts Amherst, found in their three-dimensional structural study of highly crumpled sheets. ¹

Crumpled sheets of paper are a familiar form to most of us, but they still hold many secrets. (See the article by Michael Marder, Robert Deegan, and Eran Sharon in PHYSICS TODAY, February 2007, page 33 .) Forcing a 2D sheet into a small 3D volume creates a complicated pattern of creases that resists further compression. The structure is different every time, but it is invariably mostly empty space. In their efforts to understand how a crumpled ball could be so empty yet so rigid, Cambou and Menon first tried using confocal microscopy to image microscopically thin crumpled polymer sheets. But with an x-ray computerized tomography (CT) scanner available in the geology department at nearby Amherst College, they could do the experiment much more easily with macroscopic sheets. The figure shows some 2D slices of their 3D reconstructed images.

Imaging crumpled sheets with CT scanning is not new. It was done before by Tzay-ming Hong and colleagues at National Tsing Hua University in Taiwan. ² Cambou and Menon’s contribution was to devise algorithms that would reveal the orientation and curvature of the sheet’s arrangement in 3D space. That analysis could be done on only the full 3D image, not the 2D slices. Furthermore, the crumpled sheet is locally flat almost everywhere, with a network of sharp, localized ridges, so the researchers needed an algorithm that was effective in dealing with both very low and very high curvature. “We kept thinking that there must exist standard algorithms to handle our needs,” says Menon, “but we never found any.”

As the results showed, the distributions of curvature and orientation were almost perfectly homogeneous and isotropic, despite the asymmetric nature of the crumpling. Although crumpling a sheet means compressing it from the outside, the sheet near the surface of the crumpled ball was only slightly more likely to be oriented parallel to the surface than in any other direction. Local nematic ordering—the stacking of the compacted sheet into several layers oriented in the same direction—was more prevalent near the surface than deep in the ball’s interior. But those stacks had no preferred direction.

To understand how the various features—creases, vertices, and stacks—contribute to the crumpled structure’s rigidity, Cambou and Menon are now studying not just static crumpled structures, but crumpling dynamics. For that, they have abandoned x-ray tomography, which takes several hours to produce a single 3D image, in favor of optical tomography, which is much faster.