Watching a Bose–Einstein condensate crystallize

In 1954 Robert Dicke predicted a remarkable phenomenon. Imagine a dense cloud of two-level atoms in an excited state that can radiatively decay. Because each atom typically decays independently of its neighbors, the cloud is a collection of incoherent emitters. But, he argued, if the atoms interact coherently, through the same optical field into which they emit their photons, they would spontaneously and collectively radiate coherent and highly polarized light—an effect Dicke named superradiance. ¹

Nearly a half-century later, Bose–Einstein condensates began emerging as a new tool for exploring many-body physics. Thanks to the BEC’s long coherence times, its collective motion induced by an optical field can be monitored with exquisite precision. In 1999 Wolfgang Ketterle, David Pritchard, and their MIT colleagues asked whether the motion of the atoms in a BEC can alter their interactions with an optical field. After shining laser light on a cigar-shaped condensate, the group observed dramatic superradiant bursts of scattered photons. In their scheme, a two-photon scattering process replaced what Dicke imagined as radiative decay. ² (See Physics Today, September 1999, page 17 .)

The MIT group also observed the organization of atoms into narrow momentum distributions. Photon scattering imparts a recoil momentum to atoms. But because the velocity of light is so much faster than the atomic recoil velocity—about ten orders of magnitude faster—the recoiling atoms in the experiment remained within the BEC long after their emitted photons had left and thus could affect subsequent scattering events. The upshot: Recoiling atoms interfered with condensate atoms at rest to form, in effect, a matterwave grating that enhanced the directional scattering. Photons flew off in one direction and recoiling blobs of the BEC lumbered off in another.

In that experiment, the superradiance remained limited to transient bursts. By subtly altering Dicke’s Hamiltonian, however, theorists realized as early as 1973 that a steady-state superradiant phase was also possible, even at zero temperature. Their analysis of the system’s minimum energy found that an interacting collection of atoms and photons could exhibit a second-order phase transition—crossing from a phase whose ground state contains no superradiant photons to one whose ground state does, provided the interaction is strong enough.

Now, by confining a BEC of some 10⁵ rubidium atoms in a highly reflective optical cavity and illuminating it with laser light, Tilman Esslinger and colleagues at ETH Zürich have observed the long-predicted phase transition. ³ The role of the cavity, which repeatedly reflects superradiant light through the BEC, is crucial. The cold atoms and photons influence each other through the coherent exchange of momentum à la cavity quantum electrodynamics. BEC atoms interfere to form a dynamic refractive index that diffracts the light waves. And the light waves, in turn, interfere to form an optical lattice that guides the motion of BEC atoms, as shown in figure 1. As University of Auckland theorist Howard Carmichael puts it, “The light fields tell the atoms how to move, and the atoms tell the light fields how to couple to each other.”

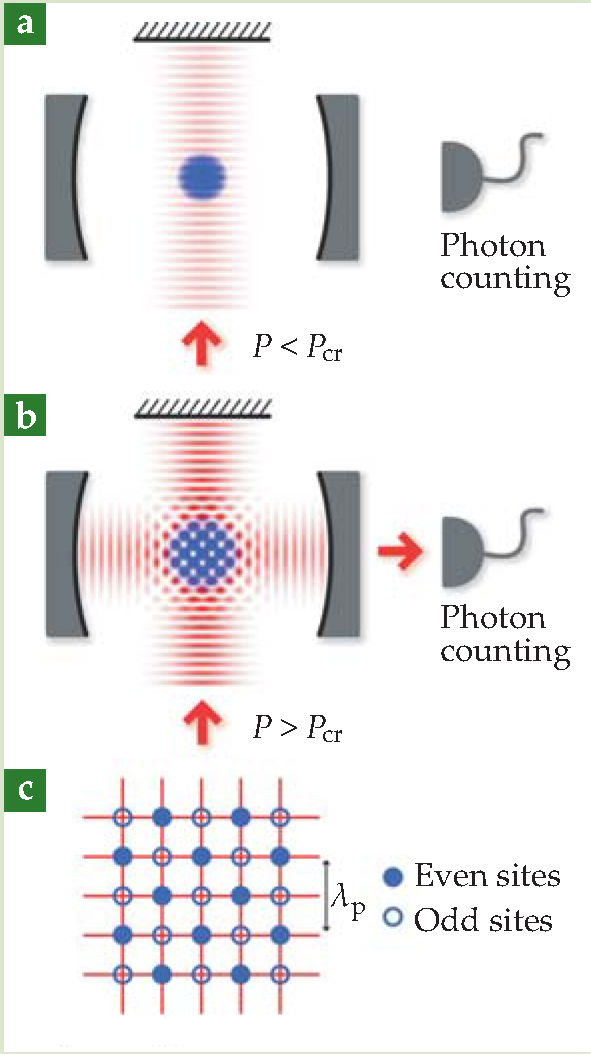
The phase transition is then manifest as a sudden shift in the BEC’s density distribution, which changes from having the character of a homogeneous superfluid to one whose long-range order is characteristic of a self-organized, crystalline state.

Light–atom crystal

The achievement builds on earlier experimental work by MIT’s Vladan Vuletić ⁴ and confirms predictions made by the University of Innsbruck’s Helmut Ritsch and Peter Domokos in the context of laser cooling of atoms in a cavity. ⁵ In 2003, working with a gas far from quantum degeneracy but in a regime in which optical forces in the cavity still overwhelm other forces acting on the atoms, Vuletić’s group found that superradiant scattering scales with the square of the number of atoms, a clear signature of self-ordering.

Four years later researchers demonstrated that a BEC can be stably trapped in an optical resonator. ⁶ That work set the stage for Esslinger’s recent experiments in which atoms and light are dynamically coupled. The emergence of self-ordering can be classified as a quantum phase transition, he argues, because the temperature is effectively zero and thermal fluctuations in the BEC are negligible.

As outlined in figure 1, when the laser power exceeds a critical value the atoms scatter the pump light by 90° into the cavity, setting up a standing wave of superradiant light whose phase depends on the atoms’ position. The interference between pump light and superradiant cavity light induces a square-lattice potential. So the relative optical phase between laser field and cavity field at the lattice sites is restricted to two values differing by π. Tiny quantum fluctuations—for example, in the cavity field or the condensate’s density—that favor one optical phase over the other prompt atoms to localize into one of the two checkerboard patterns, even or odd.

Esslinger speculates that “although the light field can then be described as a classical wave, the many-body system initially evolves into both patterns—even and odd.” Any superposition is likely to collapse nearly instantaneously, though; even a single photon leaking from the cavity early on would break the symmetry and determine the ground state.

One might expect that tuning the pump laser to one of Rb’s optical-frequency transitions would be the most straightforward route to reach the superradiant, self-organized phase. But heat from spontaneous emission created by that approach would immediately destroy the BEC. Even worse, the atom–photon coupling strength, which has to match the atomic transition energy for the phase change to happen, is many orders of magnitude too low at typical optical frequencies.

To circumvent both problems, the researchers realized they could resort to virtual (Raman) transitions, either between two electronic states of an atom, an idea proposed in 2007 by University of Auckland’s Scott Parkins, Carmichael, and their colleagues, ⁷ or between two closely spaced motional states, much like Ketterle and company did in their 1999 experiment. Choosing the latter approach, Esslinger and company tuned the laser frequency so that photon scattering would couple a zero-momentum state to one with finite momentum. It’s the interference between atoms in those two momentum states that produces density modulations.

To observe the onset of the ordered phase, they gradually increased the pump power while monitoring the light leaking out of the cavity. As long as the power remained below a critical threshold, no photons were detected outside the cavity. But above that threshold they noticed an abrupt increase in the number of photons. The time-of-flight images shown in figure 2 capture the change in symmetry in the momentum distribution of the BEC.

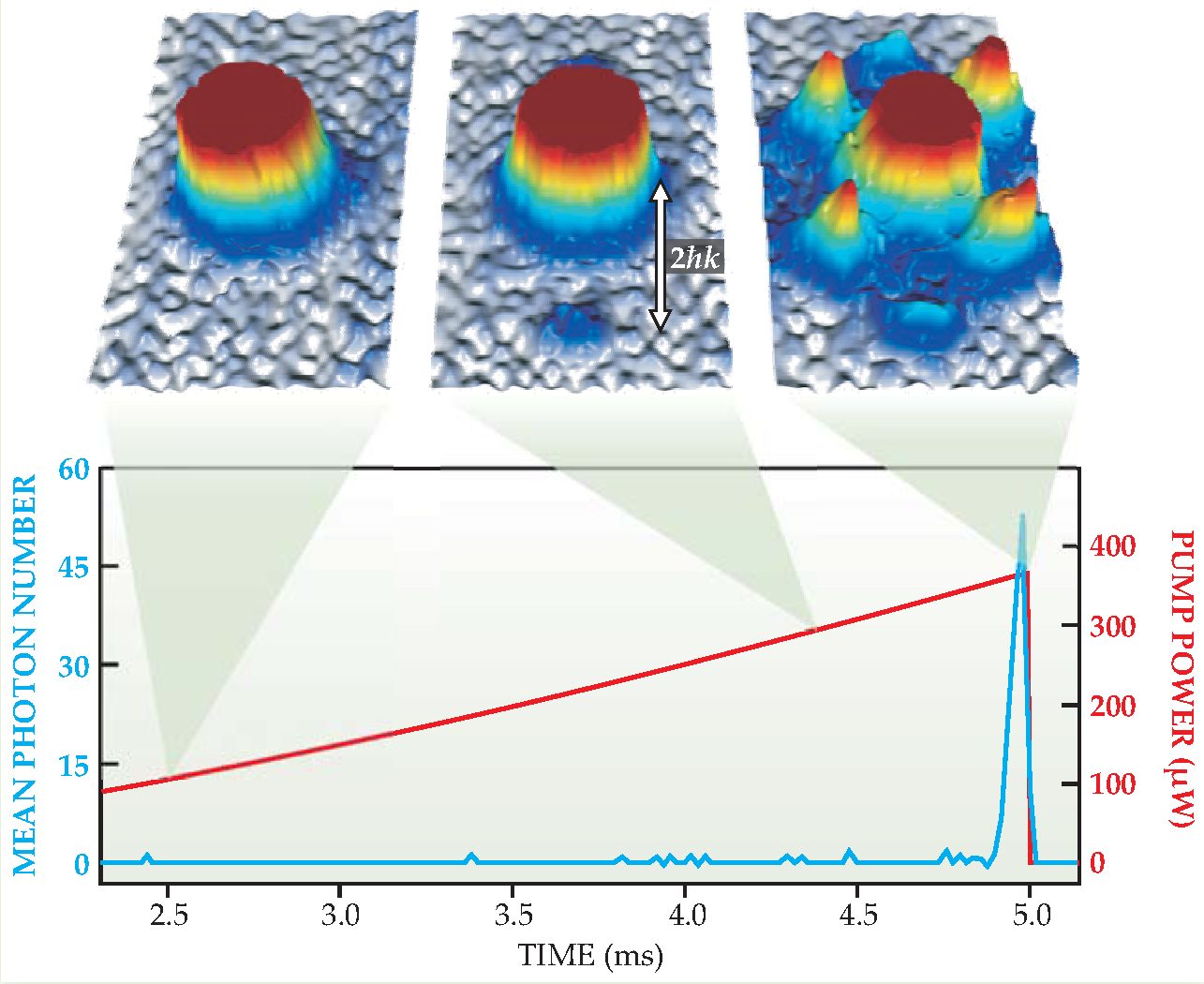
A fortunate aspect of the experiment is that the cavity output reveals time-resolved information. One experimental challenge is to probe the system’s dynamics close to the phase transition.

A new paradigm

The study of a BEC in an optical cavity represents a departure from most condensed-matter experiments, which typically probe short-range interactions among atoms. Because every atom feels the presence of every other atom via the mediating superradiant light field, the atomic interactions are truly long range: The number of nearest neighbors is effectively equal to the number of particles.

Many-body cavity-QED experiments may also provide a new perspective on phase transitions, conventionally studied in closed systems at equilibrium. Esslinger’s BEC remains in a stable ground state throughout the experiment. But the system is open, externally driven, and dissipative—far from what Dicke originally considered. That his Hamiltonian quantitatively captures the essential physics is thus all the more remarkable.