Topological phases emerge in an ecological model
DOI: 10.1063/PT.3.4695
Topology manifests itself in some of the major discoveries in condensed-matter physics of the past 50 years, including the quantum Hall effect (see the article by Joseph Avron, Daniel Osadchy, and Ruedi Seiler, Physics Today, August 2003, page 38
When a wave—for example, an electron wavefunction—travels around a topologically nontrivial path, it gains a phase after completing a closed loop rather than returning to its initial state. Although the results of the band structure’s topology are complicated to understand in detail, an essential feature is the emergence of dynamic excitations localized at the system’s boundary that are stable even in the presence of defects, a property known as robustness.
Researchers have recently started to study topological effects in systems outside hard condensed matter—for example, in liquids composed of self-propelled particles
1
and some atmospheric and ocean waves.
2
Now Erwin Frey and his group members at Ludwig-Maximilians University Munich in Germany have identified topological phases in an ecological model,
3
illustrated in figure
Figure 1.

Rock-paper-scissors model for population dynamics. Population dynamics models incorporate interactions (arrows) between different species (red spheres). Similar to other nonlinear models, they typically show extreme sensitivity to small changes in their parameters, such as the initial population size of each species. But in the rock-paper-scissors model depicted here, Erwin Frey and his students found predictable behavior regardless of parameter tweaks. That behavior derives from the topological nature of the system’s states. (Image by Cris Hohmann.)
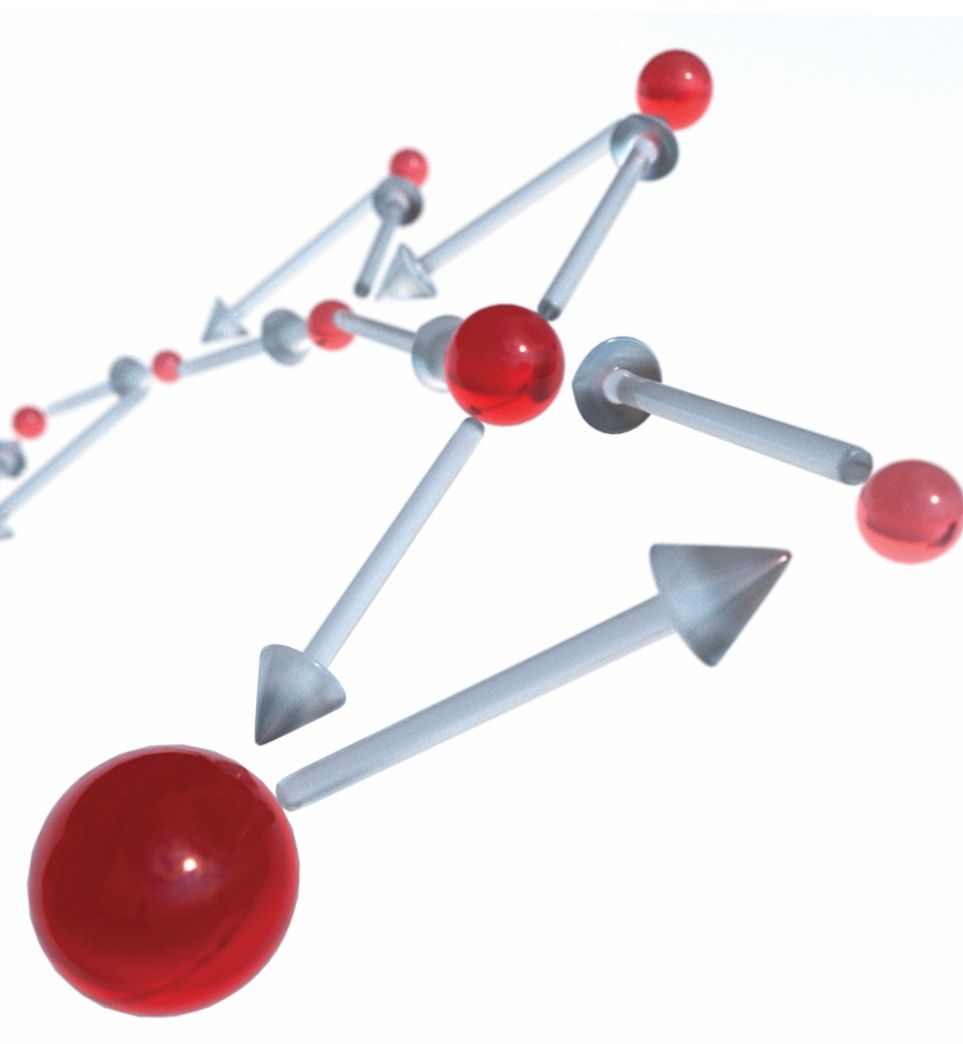
Rock-paper-scissors
Johannes Knebel, one of Frey’s graduate students, started the project in 2015 after he attended the Boulder School for Condensed Matter and Materials Physics in Colorado. While there, he was inspired by talks on topological phases in mechanical metamaterials by the University of Pennsylvania’s Tom Lubensky and the University of Chicago’s Vincenzo Vitelli and William Irvine.
One mechanical metamaterial is a lattice of gyroscopes coupled by springs (see “Topological insulators: from graphene to gyroscopes
Knebel and Philipp Geiger, another of Frey’s graduate students, had been studying one such model, the antisymmetric Lotka–Volterra equation. The ALVE is a toy model used for many different dynamic systems. In ecology, for example, it’s most often used for calculating population dynamics: how predator–prey interactions influence population growth. The Frey group recently employed it to predict the formation of Bose–Einstein condensates with species’ populations swapped for the particle population in each energetic state. 4
The ALVE can also describe an element of game theory known as a rock-paper-scissors cycle. If you picture the three moves in the game rock-paper-scissors as the points of a triangle, as seen in figure
Figure 2.

Mass polarization emerges in a one-dimensional evolutionary game-theory model inspired by the game rock-paper-scissors. (a) The model predicts the competition between S species (black points) through the mass-transfer rates r1, r2, and r3 of linked individual rock-paper-scissors cycles (gray shaded triangle). (b) Different values of the skewness r = r2/r3 yield distinct behaviors. For r = 1 the time-averaged mass distribution (gray circles) keeps its initial distribution, in this case evenly spread out. But for r < 1 the average mass gathers on the right, and for r > 1, on the left. Those topological states, in which one species dominates, manifest even with rate perturbations ε, indicated by the color of the arrows. (Adapted from ref.
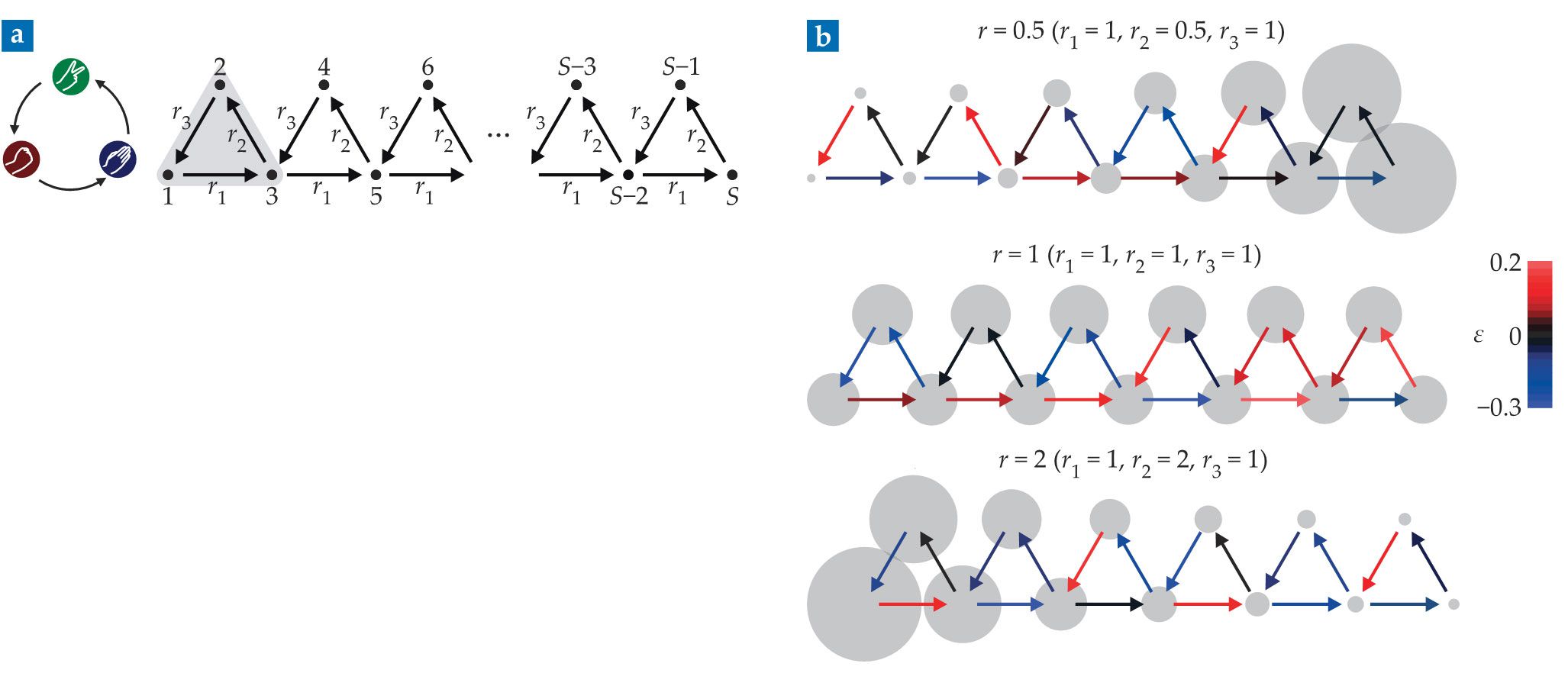
Individual cycles, such as the first one, highlighted in gray, can be assembled in different geometries, with one site for each of the S species. The mass starts in some initial configuration, and through the nonlinear interactions between the sites, it rearranges over time. The mass transfer models the system’s population dynamics.
When Frey and his students started looking for manifestations of topology in a two-dimensional lattice of rock-paper-scissors cycles, they observed chiral edge states, similar to the topological modes in 2D cold-atom lattices (see Physics Today, September 2020, page 14
Polarizing behavior
Figure
When r < 1, the time-averaged distribution of the mass (gray circles) gathers on the right, and when r > 1, the average mass gathers on the left. Although the mass averages are stable, the system is not in a rest state and remains dynamic and fluctuating about that average. The researchers call the behavior mass polarization: The average mass becomes localized and drops off exponentially with the distance from the chain’s edge. (From an ecological perspective, one species dominates the habitat.)
The skewness alone determines the mass polarization; the value of r1 and the specific values of r2 and r3 alter the quantitative but not qualitative mass distribution. What’s more, polarization states emerge regardless of the initial mass distribution and regardless of random perturbations ε to the rates, as shown by the color of the arrows in figure
When r = 1—the transition between left and right polarization states—no one species dominates, and the time-averaged mass distribution doesn’t concentrate in one spot in the chain. In figure
Those characteristics of the polarization states and transition state are topological in nature, which surprised Frey and his team. In most nonlinear dynamic models, the system’s behavior depends sensitively on the parameters and typically dissipates or becomes chaotic, essentially the opposite of the behavior they observed.
The underlying structure
To clinch the case that topology explains their observations and to relate the ALVE to condensed-matter physics, the researchers calculated the equivalent of an energy band structure for their 1D rock-paper-scissors chain. First, they formulated the interactions in terms of an S-by-S antisymmetric matrix, which served as the basis for a Hamiltonian. Frey and his students then found the eigenvalues, eigenvectors, and from those, the band structure.
Because of its Hamiltonian symmetry, the rock-paper-scissors model is related to a model Alexei Kitaev devised for 1D superconductivity. 5 Just as in the Kitaev model, an invariant characterizes the topology of the band structure. An example of a topological invariant is the genus, which classifies the number of holes in a surface. A donut has the same genus as a coffee cup and can thus smoothly deform from the one shape to the other. But a donut can’t smoothly deform into a sphere, which has a different genus.
The two skewness regimes, r < 1 and r > 1, have different values for the topological invariant and are thus topologically distinct phases. Those topological differences manifest in the mass-polarization states at the system’s boundary, an illustration of the so-called bulk–boundary correspondence that underlies topological phases.
Whether topological states will show up in real-life biological or ecological systems remains to be seen. Promising candidates are gene-regulatory networks, which consist of a collection of molecules that govern gene expression in a cell. If topological states exist, then a network would regulate selected genes unaffected by external disturbances and noise.
Frey and his students plan to apply their approach to other dynamic systems, in particular stochastic ones. Frey says he wants the important ideas of topological phases to be available to the broad readership of biological and soft condensed-matter physics. He explains, “I believe that the transfer of methods from one field of physics to a different one remains one of the most inspiring sources of innovation.”
References
1. A. Souslov, B. C. van Zuiden, D. Bartolo, V. Vitelli, Nat. Phys. 13, 1091 (2017). https://doi.org/10.1038/nphys4193
2. P. Delplace, J. B. Marston, A. Venaille, Science 358, 1075 (2017). https://doi.org/10.1126/science.aan8819
3. J. Knebel, P. M. Geiger, E. Frey, Phys. Rev. Lett. 125, 258301 (2020). https://doi.org/10.1103/PhysRevLett.125.258301
4. J. Knebel, M. F. Weber, T. Krüger, E. Frey, Nat. Commun. 6, 6977 (2015). https://doi.org/10.1038/ncomms7977
5. A. Y. Kitaev, Phys.-Usp. 44, 131 (2001). https://doi.org/10.1070/1063-7869/44/10S/S29




