The heat is on in concentrated emulsions

Emulsions—dispersions of micron-sized droplets of one liquid in another, immiscible liquid—show up in a multitude of industrial and commercial products. Mayonnaise is a familiar example. An emulsion’s shelf life—how long it lasts before, for example, the droplets start to coalesce— depends, often sensitively, on the size distribution of the droplets. Quality control therefore requires that the droplet sizes be monitored during production.

Because emulsions tend to be opaque, monitoring them optically requires that they be diluted. Ultrasound offers a less invasive alternative: The attenuation of an acoustic wave as a function of its frequency depends on the droplets’ size and number density. The conventional model for quantifying emulsions’ acoustic properties and interpreting ultrasound measurements dates back decades. ¹ But it often fails badly, especially at high droplet concentrations, because it doesn’t correctly describe how energy is converted between ultrasound and heat.

In 2012 Francine Luppé (University of Le Havre, France) and her collaborators laid the theoretical foundations for quantifying such multimode scattering through a sea of randomly distributed spherical scatterers. ² Now Valerie Pinfield (Loughborough University, UK) has built on that work to create a model explicitly relating the acoustic attenuation through an emulsion to the size and concentration of the droplets. ³

Heat waves

The scattering of an acoustic wave off a single droplet is relatively straightforward: The incident compressional wave is treated as a plane wave, the scattered wave is written as a multipole expansion of spherical harmonics, and matching the boundary conditions at the droplet’s surface gives the coefficients of the multipole expansion.

But the scattered wave isn’t purely compressional. First, if the scattering droplet’s density differs from that of the surrounding fluid, the pressure gradients of the incident wave jostle the droplet back and forth; that jostling generates shear waves. But because shear waves don’t propagate far in liquid media, their energy has—correctly—been considered to be lost from the traveling compressional wave.

Second, the alternate squeezing and relaxing of the droplet generates heat, which has also been considered lost energy. But as the heat diffuses away from the scattering droplet, the spatial distribution of thermal energy retains some of the wave’s oscillating structure for a short distance: a few microns for a 1-MHz wave, less for higher frequencies. If that thermal wave encounters another droplet before dying away entirely, it causes the new droplet to expand and contract and thereby produces a new compressional wave.

When a nonnegligible portion of an incident acoustic wave’s energy is converted from compressional to thermal to compressional, the acoustic attenuation is less than the conventional model predicts. Pinfield and her collaborators have recognized that weakness in the model for a long time. “However,” she says, “we didn’t have the mathematical tools to develop a better alternative.”

Luppé learned about the problem at a series of meetings between British and French researchers, and she decided to take it on. For a general system of spherical scatterers in a background medium (not necessarily liquid droplets dispersed in a liquid), she derived an expression for an acoustic wave’s effective wavenumber, a complex quantity whose real and imaginary parts are related to the wave’s speed and attenuation, respectively. Her formula expressed the effective wavenumber in terms of an infinite set of transition factors that describe the scattering of waves off a single particle: Each transition factor relates one of the possible incident wave modes (compressional, thermal, or shear) to one term in the multipole expansion of one mode of the outgoing wave.

Pinfield recognized that for the emulsions she was interested in, only a few of the terms in Luppé’s formula were important. First, because the liquids in an emulsion are usually close in density, multimode scattering involving shear waves could be neglected. Second, because ultrasound wavelengths are much larger than the emulsified droplets, all multipole terms higher than first order could be assumed to be zero. Third, because the processes that convert compressional waves to thermal waves and thermal to compressional operate isotropically, in those expansions only the zero-order terms are significant.

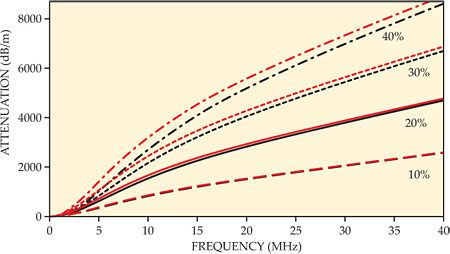
The resulting expression for the acoustic attenuation is still extremely complicated, so there’s no simple way to define the regime in which thermal waves need to be considered. Pinfield ran the numbers for some sample systems, including 0.2-µm droplets of bromohexadecane, a viscous oily liquid, in water. As shown in the figure, for a 10% volume fraction of bromohexadecane, the predictions of the conventional model and Pinfield’s new model are similar. At higher concentrations, the difference between the two models becomes progressively larger. In those systems, using the conventional model to interpret ultrasound measurements yields, as Pinfield puts it, “complete nonsense.”

Pinfield plans to conduct a thorough experimental test of her model and then to turn her attention to suspensions, or dispersions of solid particles in a liquid. Because of the density contrast between suspensions’ solid and liquid components, shear waves are an important scattering mode, and the conventional model is known to perform even more poorly, with large deviations from experiment even at 10% volume fraction of particles.