Surprising upper limit on the electron’s electric dipole moment

For decades, experimenters have been using atomic and molecular beams to measure the electric dipole moment (EDM) of the electron. As yet they’ve found no clear signal—just increasingly stringent upper limits. Those modest tabletop searches are addressing an issue crucial to particle physics, a discipline whose usual search tools are gargantuan. It’s been argued that such EDM searches are the fastest and cheapest route to the discovery of new physics beyond the standard model of particle theory.

The electron can have a nonvanishing EDM only if nature violates symmetry under time reversal (T) and under the combined operations of charge conjugation (C), which replaces particles by their antiparticles, and parity inversion (P). The standard model incorporates the small violations of CP and T symmetry that experiments at high-energy accelerators have revealed (see Physics Today, November 2012, page 16 ). But its prediction for the electron EDM’s magnitude—about 10⁻³⁸e·cm—is far too small to detect with foreseeable techniques.

It’s also very much smaller than what’s predicted by leading attempts to progress beyond the manifestly incomplete standard model and, in particular, to explain the cosmological imbalance of matter and antimatter. The range of those new-physics predictions is now accessible by molecular-beam searches.

An EDM implies some spatial separation of charges. But the electron, unlike the hadrons, is taken to be a dimensionless point particle. Its EDM is attributed to the surrounding cloud of virtual particles it continually emits and reabsorbs. And the proposed new physics predicts heavy new particles whose interactions strongly violate CP symmetry.

The electron’s EDM vector d_e must be coaxial with its intrinsic spin. A nonvanishing EDM would manifest itself by a shift −d_e·E of the electron’s energy in an electric field E. But applying a strong enough electric field to a free electron would just sweep it away. Nowadays experimenters favor highly polarizable diatomic molecules with one heavy nucleus. In such molecules, a valence electron near the heavy nucleus is subjected by a relativistic effect to a very strong intramolecular effective electric field E_eff. Three years ago Edward Hinds’s team at Imperial College London used an ytterbium fluoride beam ¹ to set an upper limit of 10⁻²⁷e·cm on the magnitude of d_e (see Physics Today, August 2011, page 12 ). The sign of d_e indicates whether the electron’s EDM is parallel (+) or antiparallel (−) to its intrinsic spin.

The 2011 limit already bit significantly into the parameter space of promising supersymmetric extensions of the standard model. But now, such “SUSY” models and a wide class of alternatives are even more hard-pressed by a new null result reported by the ACME collaboration. ² The team is headed by John Doyle and Gerald Gabrielse at Harvard University and David DeMille at Yale. With a cryogenic thorium oxide beam setup at Harvard, they have reduced the Hinds team’s upper limit by a further order of magnitude.

Measuring spin precession

The ThO molecule, much studied by the ACME team, has special advantages in the quest for d_e. When laser-excited to the rotational ground state of a particular metastable electronic state (designated the H state), the molecule can be fully polarized by a modest external electric field of order 10 V/cm. In the polarized H state, the valence electron nearest the molecule’s positively charged thorium end feels an enormous E_eff of 84 GV/cm in the direction of the oxygen end. (A second, less localized valence electron feels an E_eff that’s negligible by comparison.)

Essentially, the ACME team sought to determine d_e by looking for a tiny energy splitting 2d_eE_eff between two molecular states that differ only by whether the spin of the localized valence electron is parallel or antiparallel to E_eff. That’s done, as in the Hinds experiment, by measuring the spin precession of molecules as they traverse a region of electric and magnetic fields.

Figure 1 is a schematic of the ACME apparatus. A 50-Hz pulsed beam of ThO molecules embedded in cold neon carrier gas traces a pass through uniform magnetic and electric fields B and E pointing in the ẑ normal to the transparent electric-field plates. At the start and finish of the instrument’s 22-cm-long precession region, the molecules encounter laser beams that, respectively, initialize and read out their spin directions.

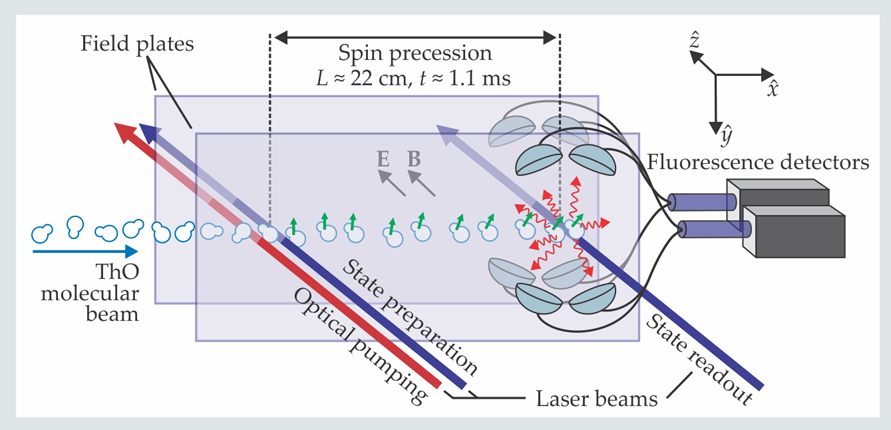
The pair of tunable initializing lasers excite ThO molecules to the polarized H state with a chosen orientation, up or down, of the molecule’s own EDM in the external E field. Choosing the polarization of the second laser prepares the H state in a particular coherent superposition of angular-momentum substates that specifies the spin precession’s starting angle.

The ¹⁶O and ²³²Th nuclei are both spinless. So in the rotationless H state, only the two unpaired valence electrons contribute to the molecule’s total angular momentum J = 1 (in units of ℏ). And when the H state is fully polarized, only the spin-aligned M = J_z substates ±1 occur.

In the B field of order 10 milligauss, the two M substates exhibit the usual Zeeman energy splitting 2μB, where μ is the polarized molecule’s magnetic moment. But the electron’s EDM, if it exists, contributes the additional splitting 2d_eE_eff that ever so slightly augments or diminishes the Zeeman splitting, depending on the sign of d_eB·E_eff (see figure 2).

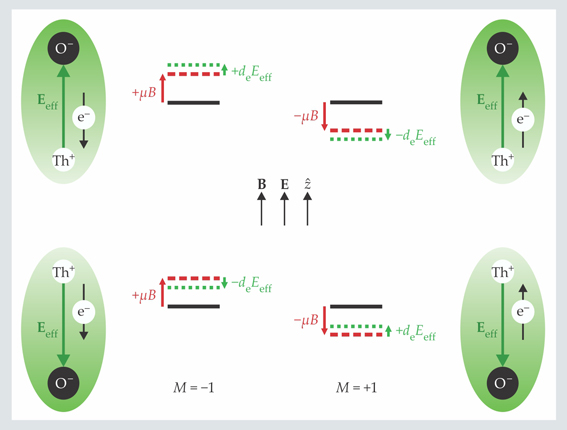
The net energy splitting between the M substates ∣+1〉 and ∣−1〉 determines the rate at which the molecule’s spin vector, viewed semiclassically, precesses in the xy-plane of the field plates en route to the downstream state-readout laser. For example, initializing the polarized H state in the coherent superposition

∣ψ(t = 0)〉 = (∣+1〉 + ∣−1〉)/√2

starts off the molecule’s spin vector pointing in the ŷ direction. But the two M substates acquire a growing phase separation as the molecule traverses the precession region, so that

∣ψ(t)〉 = (e^iϕ∣+1〉 + e^−iϕ∣−1〉)/√2,

where the phase angle ϕ(t) equals (μB ± d_eE_eff)t/ℏ. The sign between the energy terms is that of B·E_eff.

Semiclassically, one can think of ϕ(t) as the angle through which the molecule’s spin vector has precessed in the xy plane. When it’s π/2, the spin vector is aligned with the x̂ axis. The precession angle’s final value ϕ_f depends on d_e. It’s measured by the readout laser beam, whose polarization direction rapidly switches back and forth between orthogonal directions during the passage of each beam pulse.

In each polarization, the readout beam excites only the x̂ or ŷ projection of the molecule’s final precession state to a short-lived electronic state that promptly exhibits fluorescent decay. So comparing the strengths of the fluorescence signals for the two laser-polarization directions yields a measurement of ϕ_f.

Seeking tiny differences

In the quest for d_e, the team scoured the noisy ϕ_f data from millions of molecular-beam pulses measured in different combinations of E_eff, B, and E orientations, for evidence of the tiny effect of a d_e on the spin-precession rate. In the ACME experiment, the principal flipping of field orientations was done by the initializing lasers. They reversed the molecular orientation, and thus E_eff, every 25 pulses without requiring a change in the external E field. At longer intervals, the E and B fields were also reversed, to estimate and mitigate systematic errors.

Having measured the precessions of some 10¹⁰ ThO molecules during two weeks’ running last summer, the ACME team found no statistically significant evidence of the electron’s EDM. The null result yields a 90%-confidence upper limit of 8.7 × 10⁻²⁹e·cm on the absolute value of d_e.

The team attributes its 12-fold improvement on the 2011 upper limit primarily to the greater intensity and slower transit speed of ACME’s beam and the fact that ThO provides an intramolecular E_eff five times as strong as that of YbF. To extend the search below the new limit, upgrades are under way that should yield a hundredfold increase in the rate at which ThO molecules are prepared and measured.

Smaller than expected

In most suggested extensions of the standard model, a measurable d_e implies the existence of heavy new particles with masses roughly proportional to 1/√∣d_e∣. Their CP-violating interactions with electrons and other leptons could also account for the cosmological matter–antimatter asymmetry.

A d_e of 10⁻²⁶e·cm would have suggested that the new particles have masses of a few hundred GeV. That’s precisely the energy scale of electroweak symmetry breaking, where SUSY models originally anticipated the appearance of “sleptons,” supersymmetric boson partners of the leptons.

But now we learn that d_e is even smaller than 10⁻²⁸e·cm. “That’s a very significant tightening of constraints on the new physics,” says theorist Maxim Pospelov (University of Victoria, British Columbia). “It seems to disengage the anticipated CP-violating leptonic interactions from the electroweak scale. It pushes the new particles firmly into multi-TeV territory inaccessible to the next generation of sub-TeV electron–positron colliders.” Their discovery at CERN’s Large Hadron Collider remains an open question.