Superconducting qubit systems come of age
DOI: 10.1063/1.3177215
Many researchers are vying to exploit the quantum mechanical properties of superposition and entanglement to achieve massive parallel processing. They hope that a quantum computer can be far faster than today’s supercomputers and tackle problems that elude even the biggest ones.
The basic building block of a quantum computer is a two-level quantum system known as a quantum bit, or qubit. In its ground state, the qubit represents a “0” and in its excited state, a “1.” Because a qubit may be in a superposition of those states, a quantum computer with n qubits can be in an arbitrary superposition of 2 n different states simultaneously.
Physics presents no dearth of possible two-level systems as candidates for the qubits. Researchers have extensive experience with single-particle candidates such as atoms, ions, and nuclei. But they can also make qubits from solid-state systems, such as Josephson junctions or quantum dots, which exploit the macroscopic effects of quantum mechanics.
The interactions between qubits can be mediated by some kind of oscillating field. For example, atoms interact with a photon field in cavity quantum electrodynamics, and ions bound in a trap interact via their motional states. Qubits made from Josephson junctions can be coupled to a microwave resonator.
A viable quantum computer requires long-lived qubits that don’t lose their coherence before operations are completed. It also demands precise control over the qubits and their interactions, a means to interconnect a string of components, and the ability to scale up to multiple interacting qubits. Different qubit candidates have different strengths and weaknesses regarding such criteria.
The particular advantage of superconducting qubits based on Josephson junctions (sc qubits) is the very strong coupling with a microwave resonator. (See Physics Today, November 2004, page 25
Despite their relatively late entry into the race, sc qubits have caught up quickly. Two recent experiments using sc qubits demonstrate the kind of precise control required to compete in the quantum- information field.
In one experiment, John Martinis and his team at the University of California, Santa Barbara (UCSB), used their qubits to superpose on their microwave resonator any desired combination of photon-number states, which are nonclassical states of light. 1 Such states are useful for transmission and storage of quantum information. In the other recent experiment, Robert Schoelkopf and his Yale University colleagues used a pair of sc qubits to perform two simple algorithms. 2
Both experiments have been done before in some other qubit systems, but they are firsts for solid-state qubits. “The experiments illustrate in a nice way the power they have to control their systems,” notes David Wineland of NIST in Boulder, Colorado. Yasunobu Nakamura of NEC Tsukuba Research Laboratories in Japan points out a unique feature of the UCSB work: that the authors could make any arbitrary states in a deterministic and systematic way.
Superconducting qubits
Figure 1 depicts the basic components used in both experiments, except that the Yale experiment had a second qubit. The qubit is a Josephson junction, consisting of two superconductors separated by a slab of insulator thin enough for Cooper pairs to tunnel across. Experimenters can design the circuit connections for such junctions so that they form two-level systems. In a mode known as the charge mode, for example, the ground or excited level corresponds to the absence or presence of a Cooper pair; in the phase mode, the two levels correspond to phase differences across the junction. (See the article by J. Q. You and Franco Nori in Physics Today, November 2005, page 42

Figure 1. Superconducting qubit system. A circuit loop (purple) containing a Josephson junction is coupled through a capacitor to a microwave field (red) formed by a one-dimensional transmission line (green). Gaps in the transmission line reflect the microwaves and create a resonant cavity. Experimenters control the coupling of the qubit and resonator to manipulate the system.
(Adapted from A. Blais, J. M. Gambetta,

The interactions between sc qubits are mediated by a microwave resonator consisting of a one-dimensional superconducting transmission line. Gaps in the central transmission line function as mirrors to reflect the microwave, essentially trapping them in a cavity.
The qubit and resonator are placed on the same substrate, or chip, using fabrication methods honed for integrated circuits. Experimenters can tailor the system properties, like the qubit transition frequency, by manipulating the circuit elements.
Nonclassical number states
In a quantum information system, one might need to store or transfer the data contained in a qubit. For those tasks one might use a microwave field in states with definite numbers of photons—photon number, or Fock, states |n〉. Experimenters have already transmitted information from one qubit to another with microwaves in superpositions of the Fock states |0〉 and |1〉. Superpositions with higher number states might make the transfer more robust or enable the multiplexing of information.
A Fock state is a nonclassical state of light, or light that cannot be described by classical electromagnetic theory. If one drives a harmonic oscillator such as the microwave resonator with a classical signal, Martinis points out, the only control knobs are the signal’s amplitude and phase. To generate a nonclassical state requires a nonlinear element, and qubits provide that nonlinearity.
In 1996 Wineland and his group at NIST generated the first Fock states, as well as other nonclassical states. In that experiment, the Fock states were not states of radiation but of the harmonic motion of ions bound in a trap. 3
Last year, Martinis’s UCSB team used their sc qubits in the phase mode to form Fock states of their microwave resonator. With each interaction, the qubit transferred a single photon to the microwave field. Thus, n interactions generated the Fock state |n〉, with n ranging up to 15 in the UCSB experiment. 4 Independently, a team led by Serge Haroche of the École Normale Supérieure and the Collège de France, both in Paris, generated Fock states up to n = 7 in a cavity field by using the nondestructive interactions of Rydberg atoms with the cavity. 5 Both groups went further than earlier work to confirm a prediction that the decay time for the nth state varies as 1/n.
The methods used by the UCSB and Paris groups are very different. Haroche and his colleagues probe the state of the cavity field nondestructively with a stream of weakly interacting Rydberg atoms. (See Physics Today, June 2007, page 21
After generating a definite number state (by the passage of about 100 atoms), Haroche and his fellow experimenters followed the evolution of the state by monitoring the phase shifts experienced as subsequent atoms traversed the cavity. In a series of runs involving the measurement of millions of atoms, they characterized Fock states with up to seven photons.
For Martinis and his colleagues, the generation of a Fock state is more straightforward because the experimenters build up the microwave resonator field essentially photon by photon. They first decouple their qubit from the microwave resonator. After decoupling, they pump the qubit into its excited state and bring it into resonance with the microwave field so that it can transfer its excitation to the field as a single photon. Repeating the procedure a second time adds a second photon to the field, and so forth up to the desired number state.
States on demand
With their latest experiment, the UCSB team has pushed its capabilities still further by generating any superpositions of Fock states they wanted. Whereas a single Fock state |n〉 occupies only the excited level n, a superposition of Fock states has some amplitude and phase in each of the excited levels up to n.
How do the experimenters know how to populate each of those excited levels? The answer came from theoretical work done in 1996 by Chi Kwong Law and Joseph Eberly, both then at the University of Rochester. 6 Those theorists proposed a way to make a superposition of Fock states that would work no matter how many states were superposed. Wineland and his coworkers followed their prescription in 2003 to superpose four Fock states of the motion of a trapped ion. 7
The essence of the Law-Eberly prescription is to follow a step-wise procedure, in which they work down from the target state to the original state. Thus the UCSB started with the desired final superposition state, determined what they’d have to do to remove the top level, then the next level after that, and so forth down to the ground state. Because quantum mechanics is reversible in time, the team could then reverse the procedure to build up the final state. It took a while for Martinis and coworkers to calibrate their system and to get sufficient control of its elements to implement the steps, but they have now generated superpositions involving Fock states as high as n = 9 in their microwave resonator.
The experimenters verified that each number state had the expected occupancy. To probe the differences between two states such as (|0〉 + |3〉 + |6〉) and (|0〉 + i|3〉 + |6〉), however, requires a measurement that is sensitive to the quantum interferences between the different number states. The Wigner function, a measure of the quasi-probability distribution of quantum systems, is just such a tool. Unlike a classical probability distribution, it can take on negative values. (See the article by Dietrich Leibfried, Tilman Pfau, and Chris Monroe in Physics Today, April 1998, page 22
Just as x-ray tomography can piece together the internal structure of a human organ from projections made onto different slices in real space, so Wigner tomography can probe the quasi-probability distribution of a quantum wavefunction by looking at its different projections in phase space. Figure 2 presents such a distribution as a function of the complex phase space amplitude α. The two superposition states (|0〉 + |3〉 + |6〉) and (|0〉 + i|3〉 + |6〉) are indeed different. Moreover, the experimentally formed states match the expected theoretical distributions.
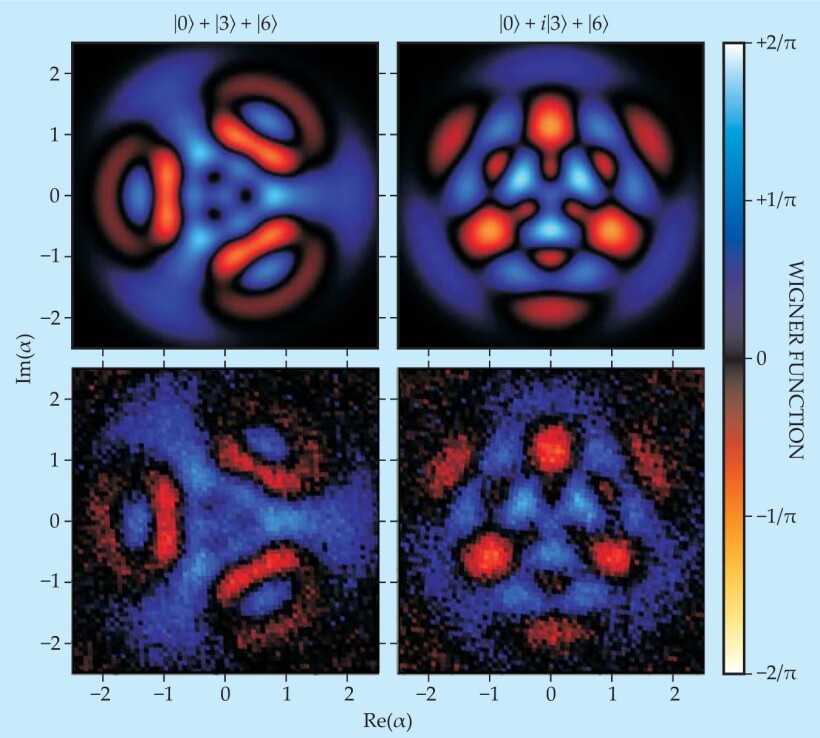
Figure 2. Wigner tomography characterizes two different superpositions of Fock states in a microwave resonator. Colors denote the values of the Wigner quasi-probability distributions for each superposition state as a function of the complex phase-space amplitude α. Negative values of the probability reflect the quantum interferences. The agreement is good between the theoretical calculations (top panels) and the experimental values (bottom panels).
(Adapted from

Quantum algorithms
In the other recent work using sc qubits, Schoelkopf and his Yale coworkers demonstrated that they could perform certain quantum algorithms with a system of two sc qubits. The qubits were located 5 mm apart and their interaction was mediated by a microwave resonator cavity coupled to both of them. The Yale group had already reported the coupling of two qubits to form a logic gate. But, as Schoelkopf points out, carrying out a sequence of logic operations required the experimenters to have qubits that remained coherent throughout the chain of interactions, qubit interactions that they could turn on and off quickly, and the ability to address each qubit individually.
The Yale experimenters satisfied the last two requirements by running a separate control wire to each qubit. The current on the control wire determined the flux through each qubit and hence its operating frequency. With an appropriate choice of current pulses on the control wires, the researchers could quickly turn on the two-qubit interaction.
That interaction was mediated by the exchange of a virtual photon rather than a real one in the microwave resonator cavity. As explained by lead author Leo DiCarlo, the interaction made the transition frequency of one qubit depend on the state, |0〉 or |1〉, of the other. That interaction allowed the realization of a basic two-qubit operation known as a conditional phase gate.
Using that basic logic gate, the Yale team formulated the set of logic steps to carry out two celebrated quantum calculations: the Grover search and the Deutsch–Josza algorithms. The former is a quantum algorithm that enables someone searching an unsorted database with N entries to find the answer after a number of tries on the order of N 1/2. Classically, the search would require on the order of N tries. The Deutsch-Josza algorithm is a way to determine with just one look at a coin whether the two sides of the coin are different or the same.
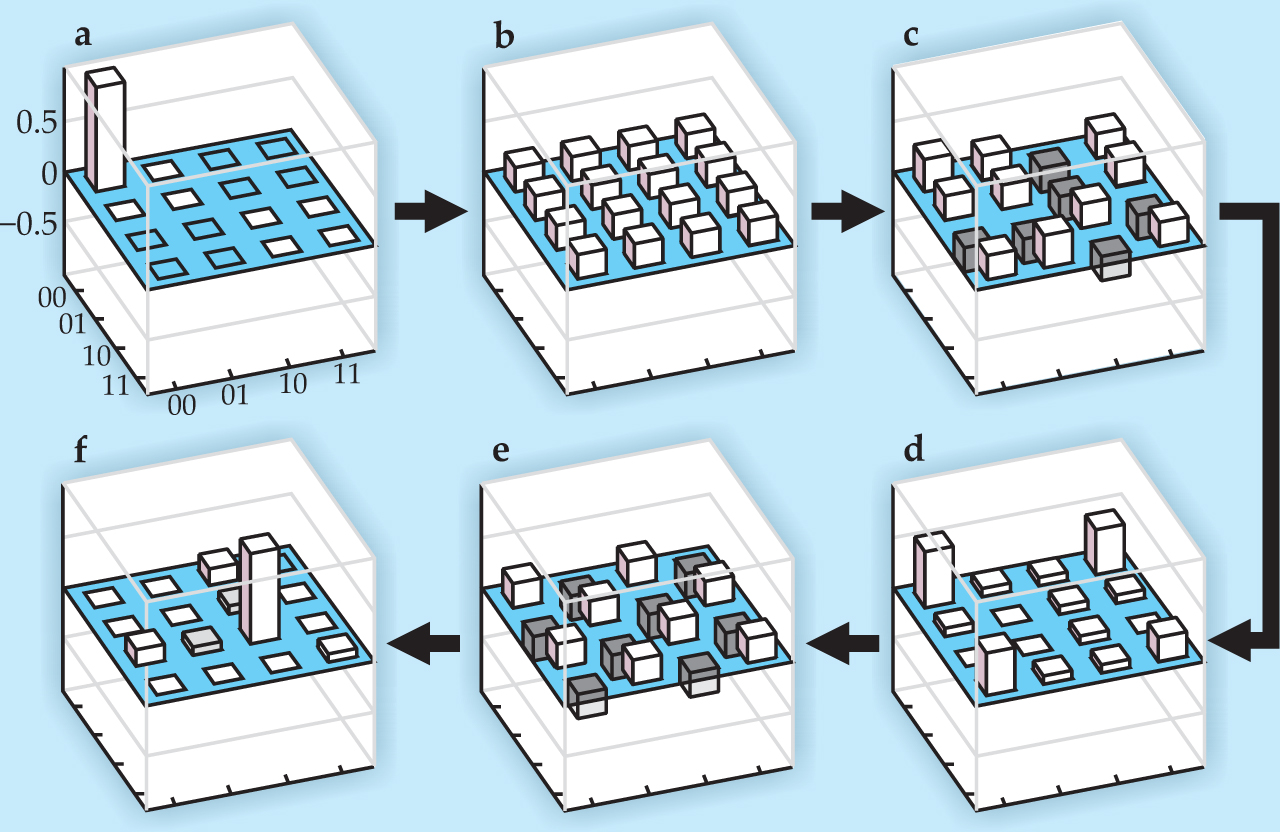
Figure 3 shows in clockwise order the states of the two-qubit system during various stages of the Grover search algorithm, starting with the ground state in figure

Figure 3. The Grover algorithm is implemented in six steps, shown in clockwise order. Each panel depicts the occupation of each state as a function of the four basis states, |0,0〉, |0,1〉, |1,0〉, and |1,1〉. (a) Both qubits start in the ground state. (b) The qubits are put into maximal superposition states. (c–e) Qubit interactions entangle and unentangle the qubits. (f) The final state contains the correct answer with 85% fidelity.
(Adapted from
Can the system be scaled up by simply adding a third qubit in line with the first two? Three qubits is not just more of the same, says Schoelkopf. With three qubits, you can have new types of entanglement and begin to investigate simple forms of quantum error correction. A major limitation to scaling up the systems is the short qubit lifetime. John Clarke of the University of California, Berkeley, notes that the US Intelligence Advanced Research Projects Activity has a new initiative to increase sc-qubit coherence times. Positive results from that initiative would give an additional boost to sc-qubit systems.
References
1. M. Hofheinz et al., Nature 459, 546 (2009). https://doi.org/10.1038/nature08005
2. L. DiCarlo et al., Nature (in press).
3. D. M. Meekhof et al., Phys. Rev. Lett. 76, 1796 (1996). https://doi.org/10.1103/PhysRevLett.76.1796
4. M. Hofheinz et al., Nature 454, 310 (2008); https://doi.org/10.1038/nature07136
H. Wang et al., Phys. Rev. Lett. 101, 240401 (2008). https://doi.org/10.1103/PhysRevLett.101.2404015. S. Deléglise et al., Nature 455, 510 (2008);
M. Brune et al., Phys. Rev. Lett. 101, 240402 (2008). https://doi.org/10.1103/PhysRevLett.101.2404026. C. K. Law J. H. Eberly, Phys. Rev. Lett. 76, 1055 (1996). https://doi.org/10.1103/PhysRevLett.76.1055
7. A. Ben-Kish et al., Phys. Rev. Lett. 90, 037902 (2003). https://doi.org/10.1103/PhysRevLett.90.037902




