Putting quantum gases under the microscope

Many intriguing behaviors, such as high-temperature superconductivity, result from the strong interactions among particles in a many-body system. Theorists have explored those complex interactions with model Hamiltonians, but real-world defects make physical systems imperfect realizations of the models. And time and memory constraints limit computer simulations of quantum behavior to just a handful of atoms.

A tantalizing alternative is to use small clouds of atoms, typically tens of thousands, cooled to nanokelvin temperatures, to study the complex physics of strongly correlated systems. To simulate the structure of solids, researchers can trap atomic gases in a periodic array of optical potentials created by intersecting laser beams, much as eggs are confined by the corrugations of an egg carton. The optical arrays can be nearly defect free, and particle interactions can be tuned to explore the system behavior. Depending on whether the atom is a fermion or a boson, it might represent an electron or an electron pair. The simulations can possibly be extended to quantum spin systems, such as antiferromagnetic systems or spin liquids, if experimenters can get down to 100 pK temperatures.

Until recently, however, experimenters could only measure densities averaged over many lattice sites, making it difficult to obtain accurate information about many important system properties such as the equation of state or the temperature. Experimenters lacked the insight that would come from knowing the local properties of each atom. Such insight is now provided by newly published fluorescent-microscope images that give single-site resolution of quantum gases of rubidium atoms in optical lattices. The images from two experiments confirm visually what had previously been inferred indirectly (see Physics Today, March 2002, page 18 ) about the transition from a superfluid phase, such as a Bose-Einstein condensate (BEC), to a Mott insulator (MI) phase. (An MI does not carry current because particle interactions inhibit hopping between sites.) The new experiments were done by Markus Greiner and his colleagues at Harvard University ¹ and by a group under the direction of Stefan Kuhr and Immanuel Bloch of the Max Planck Institute of Quantum Optics in Garching, Germany. ²

Single-atom snapshots

Although images have been made of ions in various kinds of traps and of small numbers of individual atoms, until recently no one had resolved single atoms in a large collection of atoms. Recently, electron beams were used both to address and to make high-resolution images of atoms in a two-dimensional BEC, but each lattice site held up to 80 atoms. ³ In 2007, David Weiss and coworkers at the Pennsylvania State University produced fluorescent images that resolved single atoms sitting in successive planes of a 3D lattice, with 250 atoms total. ⁴ The team members were motivated by their interest in using atoms in the 3D lattice as qubits for quantum information processing, an application that requires a means both to address and to manipulate single atoms.

To apply fluorescent microscopes to cold-atom simulations of strongly correlated systems, researchers need to resolve lattice sites that are much more closely spaced than in the Penn State experiment (0.5 µm versus 5.0 µm): Only at those shorter distances do particles tunnel and interact strongly. Researchers also had to incorporate the required high-resolution microscope into an all-optical trap designed to produce a very cold, quantum degenerate gas.

Last year Greiner and coworkers introduced a fluorescent microscope of unique design having a resolution on the order of half a micron, roughly the size of the lattices to be studied. ⁵ Their more recent work, together with that of the Max Planck group, shows unambiguously that atoms, which freely move around within a BEC, freeze in regions of constant density within an MI.

The high-resolution microscopes have created quite a buzz, especially among those researchers who hope to use quantum gases to explore a variety of model Hamiltonians. Wolfgang Ketterle of MIT likens the new tool’s impact to that of scanning probe microscopes on condensed-matter systems: Those probes provide real-space pictures to complement momentum-space measurements.

Fluorescent microscopes

The high-resolution fluorescent microscope designed by the Greiner group is sketched in figure 1. After forming the optical trap with a holographic phase mask, the team controls the state of the gas (BEC or MI) by tuning the depth of the potential wells in the optical lattice. Before taking a snapshot of the atoms in a given phase, the experimenters want to be sure that their subjects don’t move during the exposure. Thus, they very quickly deepen the lattice’s potential wells a thousandfold to pin each atom in place. They then turn on an arrangement of polarized lasers known as an optical molasses. Atoms in the lattice inelastically scatter the photons in the molasses, producing fluorescence. Typically, one atom will scatter thousands of photons per image.

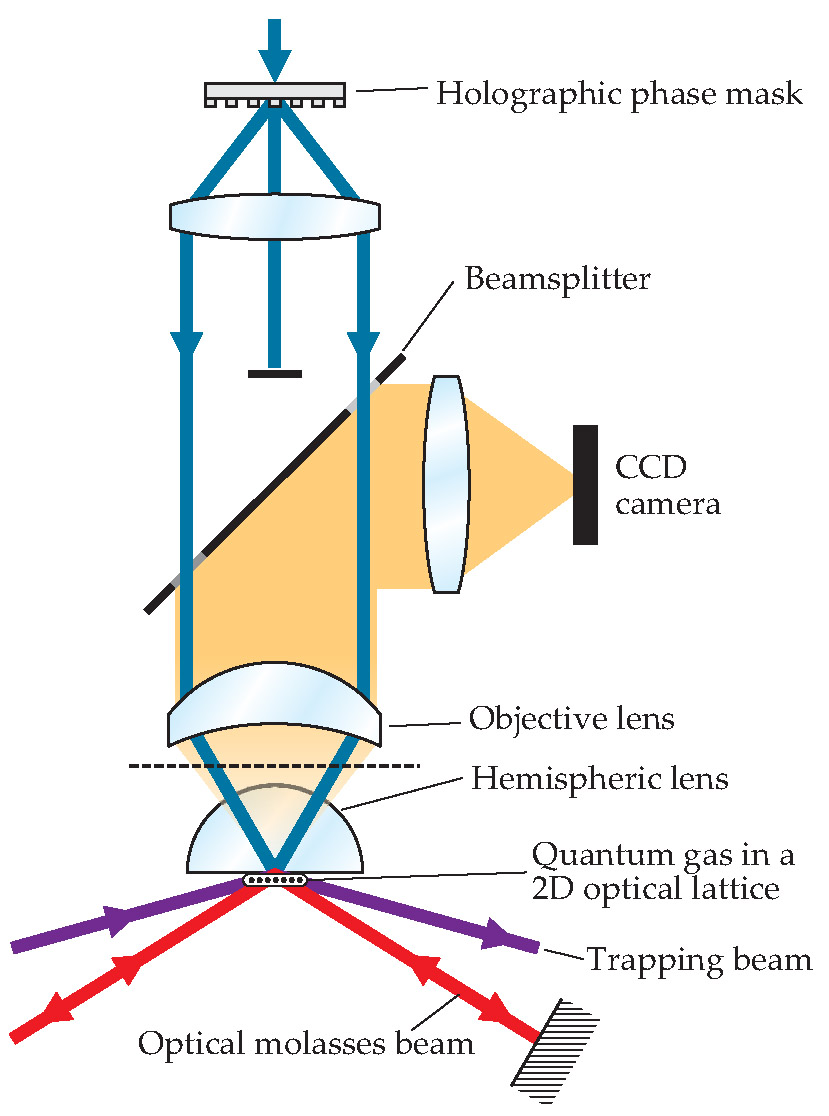
The scattered light is collected by a high-resolution imaging system consisting of both an objective lens outside the vacuum chamber and a hemispheric lens inside it. The hemispheric lens increases the numerical aperture, a measure of the angle over which a lens can collect light. The resulting large numerical aperture (0.8) contributes to both greater light collection and higher resolution (0.6 µm).

Kuhr, Bloch, and coworkers used a similar apparatus and procedure except that they relied on interfering laser beams rather than on a holographic mask to generate the optical lattice. In addition, the Max Planck team used a single high-quality objective lens with a numerical aperture of 0.68 and a resolution of 0.7 µm.

The fluorescent microscopes actually do not determine the total occupancy of each lattice site, which typically holds more than one atom. That’s because the optical molasses beams promote inelastic collisions between pairs of atoms and scatter those pairs out of the trap. As a result, each site is left with one or no atoms, depending on whether it was initially occupied by an odd or even number of atoms. Hence, the images record the parity of the atom number.

The Mott insulator

The cold-atom lattices studied in the Harvard and Max Planck experiments can be described by the Bose-Hubbard model. According to that model, atoms are governed by only two parameters: the interaction U when two atoms occupy the same site and the strength of tunneling J between lattice sites. The experimenters can control J and hence the ratio U/J by changing the depth of the potential wells in the optical lattice. When the ratio is low as in the super-fluid phase, hopping is prevalent. As the ratio increases, atoms are pinned more strongly by the lattice and the system transitions to an MI, with the atoms essentially frozen in place. The recent experiments explored that transition. Although their findings yielded few surprises, “Still they are amazing to see,” commented Pierre Meystre at the University of Arizona. “The pictures are gorgeous.”

The images in figure 2, taken by the Harvard microscope, show a small region of a quantum gas in both the BEC and the MI phases. Shown are both the direct images and the result of an algorithm that determines which of the 10 × 8 lattice sites are occupied. Because atoms in a BEC freely hop from one site to another, they are delocalized across the entire lattice. On each site then it is equally likely to find an even or an odd number of atoms, hence the average measured site parity p is about 0.5. In the MI phase shown, atoms are fixed in place with all the sites singly occupied, so that p approaches 1 or 0.

Wider fields of view, such as the reconstructed images in figure 3, reveal the shell structure predicted for the MI. Theory predicts that as more atoms are added to the MI, the energy to put an atom in a lattice site outside a certain radius exceeds that for adding a second atom to the inner core. The resulting shell, or wedding cake, structure had been seen before ^{6 – 8} but never quite so visually.

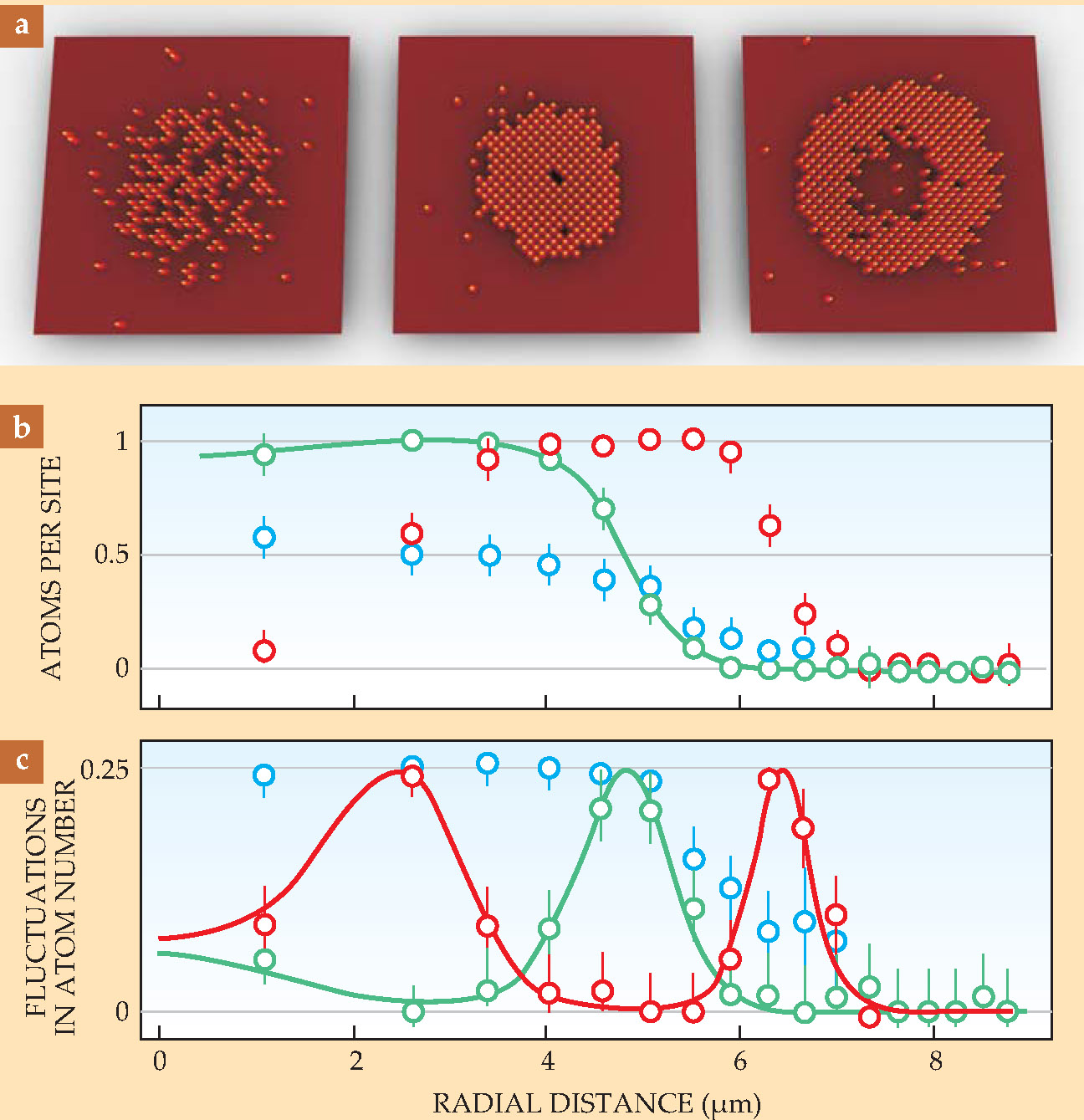
The radial atom-number distribution within the observed shells is plotted in figure 3 for the BEC and the two MI phases shown in the top panel. As expected, p is approximately 0.5 for a BEC and approaches either 0 or 1 within an MI region. Also shown is the variance in those number distributions. The BEC is characterized by large fluctuations because atoms are free to hop from site to site. Large fluctuations also show up in relatively narrow regions just outside each MI shell. The low fluctuations in the MI regions indicate that the entropy is close to zero there: Those regions have dumped their entropy into the surrounding shells.

If the images from the Harvard and Max Planck groups offer any surprise, it is the sharpness of the transition region—both in space and in time—between the MI and the superfluid BEC. Spatially, some MI regions are only a few lattice sites wide. Temporally, the system is found to go from a BEC to an MI phase in a few milliseconds. Greiner is amazed that the atoms can arrange themselves so quickly, exactly filling all the right lattice sites.

The transfer of entropy out of the MI regions has given a number of experimenters an idea for further cooling. As explained by Greiner, ejecting those atoms just outside a core MI region can get rid of all that entropy. The new cooling regime might then reach the low enough temperatures for experiments on quantum spin systems.

In addition to trying to get to lower temperatures, the experimenters are working to extend their imaging capabilities to 3D. They are also exploring ways to manipulate the atoms, especially for applications to quantum computing.