Powerful lasers mimic intergalactic plasmas in the lab
DOI: 10.1063/PT.3.2901
Magnetic fields in intergalactic space—revealed through synchrotron radiation from cosmic relativistic electrons—are stronger than one might expect. At up to tens of microgauss, they carry a significant fraction of the energy in the rarefied plasmas they pervade. (See the article by Philipp Kronberg, Physics Today, December 2002, page 40
Although the origin of the fields is still largely a mystery, theorists have some ideas about how they might arise. One favorite model begins with the Biermann battery mechanism: Plasma temperature and pressure gradients pointing in different directions generate a net electric current, which creates minute magnetic fields of about 10−21 G. Those seed fields are then amplified by turbulence: When the plasma is churned—in a collision between galaxy clusters, for example—the field lines remain pinned to their plasma, so they stretch and twist. As individual field lines are elongated, their overall spatial density—and thus the field—becomes greater. Eventually, theory predicts, the process becomes self-sustaining: a so-called turbulent dynamo.
That mechanism works well enough in numerical simulations, but confirming it observationally is complicated by the multimillion-year time scales of intergalactic events. Happily, though, the magnetohydrodynamic equations that govern plasma behavior are scale invariant. 1 So it should be possible to create a smaller, faster analogue of a turbulent astrophysical plasma in the lab.
Now Oxford University’s Gianluca Gregori, his recently graduated PhD student Jena Meinecke, and a team of collaborators have done just that. 2 Working at the Rutherford Appleton Laboratory’s Central Laser Facility, shown in figure 1, the researchers focused 240-J laser pulses onto each of two carbon foils to create a pair of opposing plasma jets. The jets collide in a puff of turbulence after traversing a few centimeters in a little less than a microsecond—and thus mimic the merging of a pair of galaxy clusters over hundreds of millions of years. In the wake of the collision, the researchers see signs of the beginning of turbulent magnetic amplification.

Figure 1. At the Rutherford Appleton Laboratory’s Central Laser Facility, Jena Meinecke arranges 8-inch-diameter optics to focus the powerful Vulcan laser onto two carbon-foil targets. Before each laser shot, the entire chamber is locked down and filled with argon gas.
STEPHEN KILL, STFC

Turbulence large and small
Gregori and company didn’t set out to study galaxy-cluster collisions. When they arrived at the Rutherford Appleton Laboratory last year for their five-week scheduled experiment, they intended to mimic smaller-scale astrophysical plasma phenomena—namely, how a shock wave created during a supernova might generate turbulence that temporarily amplifies the surrounding magnetic field to a few milligauss. 3 That turbulent amplification plays out over centuries in supernova remnants several light-years across.
The idea of using laser experiments to study aspects of supernovae and supernova remnants is more than 15 years old. 4 But the Oxford researchers’ experiment took a turn for the unexpected in its third week when they tried to generate two interpenetrating shock waves by firing beams from the laser at two opposing targets. “What resulted instead, due to the laser configuration, were two jets,” says Meinecke. “That was a surprise to us at the time. We didn’t fully understand what our results meant until months afterward.” The connection to galaxy clusters, a system less explored by laser astrophysicists, was ultimately made by their colleague Alexander Schekochihin, also an author on the new paper.
Galaxy clusters are the largest gravitationally bound structures in the universe. The vast majority of their mass—not counting dark matter—exists not in the form of stars and planets but as a diffuse plasma within and between the cluster’s galaxies. Though they comprise just a few dozen atoms per cubic meter, the plasmas are still hundreds of times as dense as the medium outside the cluster. So the merging of two galaxy clusters can be reasonably well simulated by the collision of two featureless plasma blobs.
Plasma magnetism
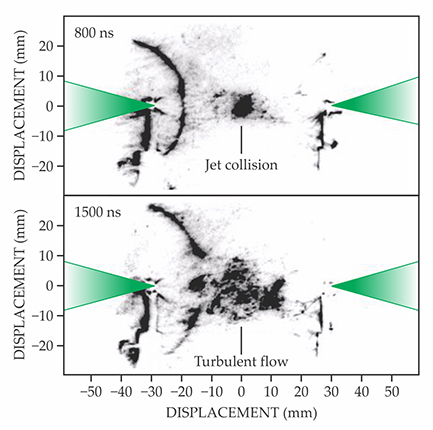
Gregori and company characterized their plasma system using Schlieren imaging—an optical technique using collimated backlighting to reveal density gradients in the plasma—and tracked the magnetic field using a handmade induction probe positioned near the midpoint between the two targets. The Schlieren images in figure 2 show the jets colliding 800 ns after the laser pulse and a region of turbulent flow developing 700 ns later.
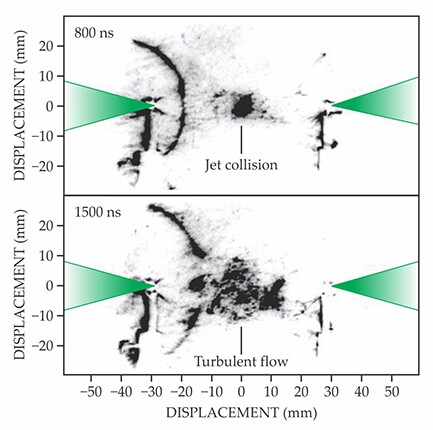
Figure 2. Focused pulsed laser beams, represented by the green triangles, launch a pair of plasma jets. The jets collide 800 ns after each laser pulse, and a region of turbulence develops within another 700 ns. (Adapted from ref.
The magnetic-probe data show the field being turbulently amplified, but only marginally. Firing a single jet, with no turbulent collision, produces a field that peaks near 10 G. Scale the system up to the size of a galaxy cluster, and that’s approximately equivalent to the 10−21 G that numerical simulations say can be produced by the Biermann battery mechanism. 5 A two-jet collision yields a field two to three times as strong—nowhere near the quadrillionfold amplification that needs to occur astrophysically.
That difference can be attributed to the electrical properties of the plasma. Sustaining a turbulent dynamo requires the plasma to be nearly perfectly conducting to pin the magnetic field lines to the turbulent flow. Too much electrical resistance and the field lines start to slip. The role of the resistivity is quantified by a dimensionless parameter called the magnetic Reynolds number Rm: The higher the Rm, the more closely the field lines move with the plasma. Intergalactic plasmas are estimated to have an Rm of more than 200. In the Oxford researchers’ experiment, Rm is about 14.
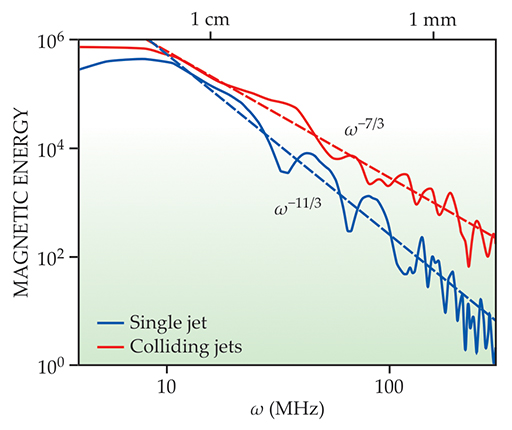
To conclude that they’re seeing turbulent amplification at all, the researchers needed to probe their data a bit deeper. Figure 3 shows the magnetic energy spectrum, the absolute square of the magnetic field’s Fourier transform. In the single-jet experiments, the field is strongest in low-frequency components and falls off rapidly at higher frequencies. In the two-jet case, the spectrum’s shallower slope—approaching those found in numerical studies of astrophysical plasmas 6 —suggests that the field lines are starting to get tangled up with the turbulence.
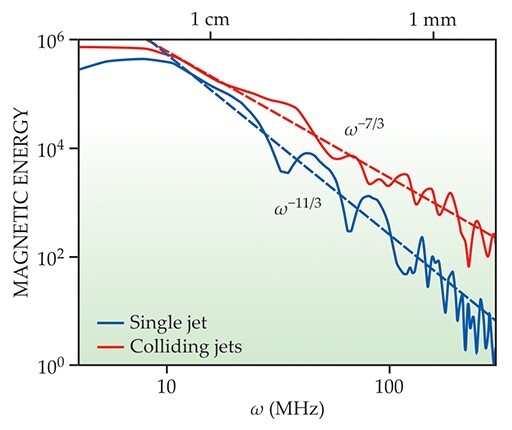
Figure 3. The magnetic energy spectrum is the absolute square of a magnetic field’s Fourier transform. In experiments in which only a single plasma jet is fired, most of the magnetic energy is concentrated in low-frequency, large-scale components, and the spectrum falls off rapidly as the frequency ω increases. In a turbulent collision of two jets, the slope of the spectrum is much shallower—a putative sign of the beginning of magnetic turbulent amplification. (Adapted from ref.
The ultimate goal is to access a regime of high enough Rm to see a full-fledged turbulent dynamo. Toward that end, Cary Forest and colleagues at the University of Wisconsin–Madison have recently opened a new user facility, the Wisconsin Plasma Astrophysics Laboratory, for mimicking various astrophysical plasma phenomena, including turbulence at the galaxy-cluster scale. 7 “We are also working on parts of the dynamo problem,” explains Forest, “but our experiment is quite different in that we create plasmas that are quasi-stationary, not impulsive.”
For their part, Gregori, Meinecke, and their collaborators are planning to repeat their experiments next year at the National Ignition Facility in Livermore, California, where they can make hotter, and thus more conductive, plasmas. “We want to know when turbulent dynamo sets in, how it affects the magnetic field, and how it develops over time,” says Meinecke. “Those insights could unlock the secrets behind astrophysical events and the origins of magnetic fields in the universe.”
References
1. D. Ryutov et al., Astrophys. J. 518, 821 (1999); https://doi.org/10.1086/307293
J. E. Cross, B. Reville, G. Gregori, Astrophys. J. 795, 59 (2014). https://doi.org/10.1088/0004-637X/795/1/592. J. Meinecke et al., Proc. Natl. Acad. Sci. USA 112, 8211 (2015). https://doi.org/10.1073/pnas.1502079112
3. J. Meinecke et al., Nat. Phys. 10, 520 (2014). https://doi.org/10.1038/nphys2978
4. B. A. Remington et al., Phys. Plasmas 7, 1641 (2000). https://doi.org/10.1063/1.874046
5. G. Gregori et al., Nature 481, 480 (2012). https://doi.org/10.1038/nature10747
6. A. A. Schekochihin et al., New J. Phys. 9, 300 (2007). https://doi.org/10.1088/1367-2630/9/8/300
7. C. B. Forest et al., J. Plasma Phys. 81, 345810501 (2015).https://doi.org/10.1017/S0022377815000975
More about the authors
Johanna L. Miller, jmiller@aip.org




