Optical cycling paves the way for laser-cooled molecules

Laser cooling of atoms enables a great deal of ultracold physics. In its most widespread form, called Doppler cooling, a sample of atoms is irradiated from all sides with laser light whose frequency is tuned just below an atomic resonance. Each atom preferentially absorbs photons that are blueshifted into resonance—that is, the ones that oppose the atom’s motion. The atom then reradiates the light in a random direction and returns to its ground state. Repeating that optical cycle some tens of thousands of times can cool the atomic sample to below 1 mK.

Cooling of molecules, particularly molecules comprising more than one type of atom, to ultracold temperatures could expand the potential for studies of ultracold chemistry or even for a quantum computer that uses molecules as qubits. Doppler cooling is tricky to apply to molecules—for a long time it was believed to be close to impossible—so researchers focused on making ultracold molecules in other ways, such as by assembling them out of ultracold atoms. But the only molecules that have been created in that way are pairs of alkali metal atoms.

Now, David DeMille and colleagues at Yale University have demonstrated optical cycling—the principal requirement for Doppler cooling—of a diatomic molecule, thereby opening up a new class of molecules to possible ultracold study. ¹ Explains Bretislav Friedrich of the Fritz Haber Institute of the Max Planck Society in Berlin, “People had gotten used to regarding the prospects for laser cooling molecules as bleak. This work demonstrates beautifully that the lack of a key ingredient can be overcome in a molecule after all.”

Cool as a molecule

Molecules of two or more atoms have rotational and vibrational degrees of freedom that split each of their electronic quantum states into a multitude of long-lived, low-lying states. When an excited molecule is allowed to decay, there’s generally no way to know in which one of many states it will end up. A successful Doppler cooling scheme cannot allow molecules to accumulate in any state that’s not excited by a laser. But exciting every possible rotational and vibrational level individually would be prohibitively difficult. Dozens or even hundreds of different laser frequencies would be required.

In 2004 Michael Di Rosa of Los Alamos National Laboratory solved part of the problem when he noticed that certain molecules, including monohydrides and monohalides of alkaline earth metals, almost always return to the vibrational level from which they were excited. ² Their Franck–Condon factors f_ij —the absolute square of the wave function overlap integral between the ith vibrational level of the ground state and the jth vibrational level of the excited state, and a measure of the likelihood of each state-to-state transition—form a nearly diagonal array. That fortunate circumstance arises because each of those molecules has an electron outside the outermost closed shell. Because the extra electron makes only a small contribution to the chemical bond, exciting it doesn’t change the vibrational wavefunctions much.

The problem of rotational levels was addressed in 2008 by Jun Ye and colleagues at JILA in Boulder, Colorado. ³ A photon carries one quantum of angular momentum, so when a molecule absorbs or emits a photon, its angular momentum quantum number J can change by 1, −1, or 0. Ye and colleagues pointed out that there are ways of forbidding some of those possibilities. For example, in some molecules, the minimum J for the excited state is some J _min and the minimum J for the ground state is J _min + 1. So when the molecule is excited into the state with J = J _min there’s only one level into which it is allowed to decay.

Best of both worlds

DeMille, who had been working on assembling bialkali molecules from ultracold atoms, read about Ye and colleagues’ work and was reminded of Di Rosa’s. He thought that Di Rosa’s scheme required too many lasers to be practical and that the titanium monoxide used in the JILA group’s scheme had too long-lived an excited state. But perhaps, he thought, he could combine features of each.

Together with postdoc Edward Shuman and graduate students John Barry and David Glenn, DeMille began in the fall of 2008 to set up an experiment using strontium monofluoride, one of Di Rosa’s class of molecules, and restricting the allowed rotational transitions using a strategy similar to Ye and colleagues’. The group had its first results within a year. “This is, I think, the fastest I’ve ever taken an experiment from concept to completion,” says DeMille.

The relevant energy levels and Franck–Condon factors of SrF are shown in figure 1. From the excited state’s lowest vibrational level (in which ν′, the vibrational quantum number, equals zero), 98% of molecules decay to the ν = 0 level of the ground state, while 2% are lost to other levels, mostly ν = 1. Exciting only molecules in the ν = 0 level would lose most of the molecules to unexcited states after only 50 absorption-emission cycles. Adding a second laser tuned to excite the ν = 1 level kept the cycling going much longer.

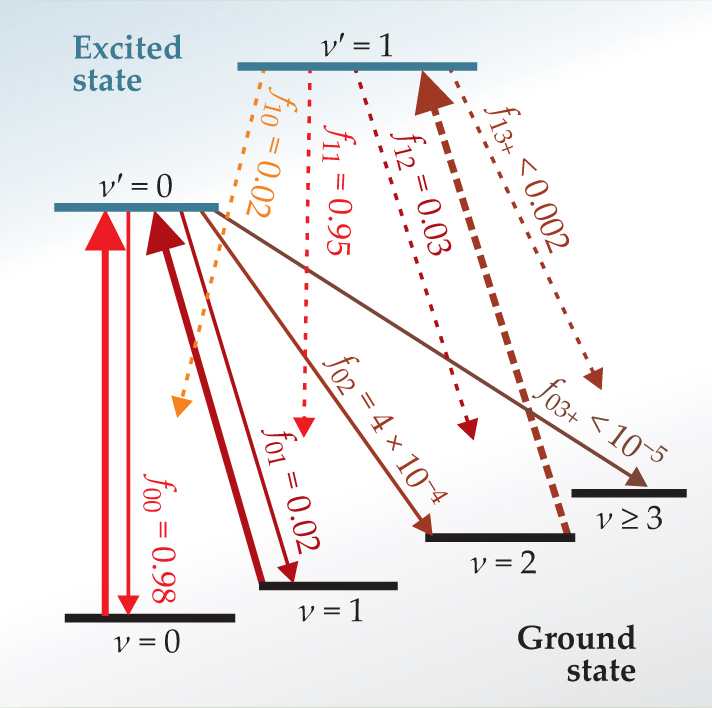
The Yale researchers focused on the rotational quantum number N rather than the total angular momentum quantum number J. They excited molecules from the N = 1 level of the ground state to the N = 0 level of the excited state. The molecules cannot decay to N = −1 (since there is no such thing) or N = 0 (since it happens to be forbidden by parity), so they must return to N = 1. Not all molecules start out with N = 1, and those that don’t are invisible to the cycling scheme. “That is not so different from many systems of laser-cooled atoms,” explains DeMille, “where often less abundant isotopes are used and the rest are ignored or thrown away. But there are ways to put more of the population into N = 1 if we need to.”

Beam deflection

Two complications remained. First, the interaction of nuclear, electronic, and spin angular momentum splits the ν = 0, N = 1 level of the SrF ground state into four hyperfine sublevels, each of which would have to be excited separately. Luckily, there was an easy solution: A single laser beam, passed through a so-called electro-optic modulator, could be split into four frequency components that matched the hyperfine splitting almost exactly.

The second complication was the existence of dark Zeeman sublevels. For an excitation that decreases the molecule’s angular momentum, there necessarily exist linear combinations of the degenerate ground-state Zeeman levels whose transition amplitudes interfere destructively. Molecules in those states can’t absorb light. Ye and colleagues proposed mixing the states with a pulsed electric field; DeMille and company instead chose a weak magnetic field, which lifts the degeneracy and pushes the molecules in and out of the dark states.

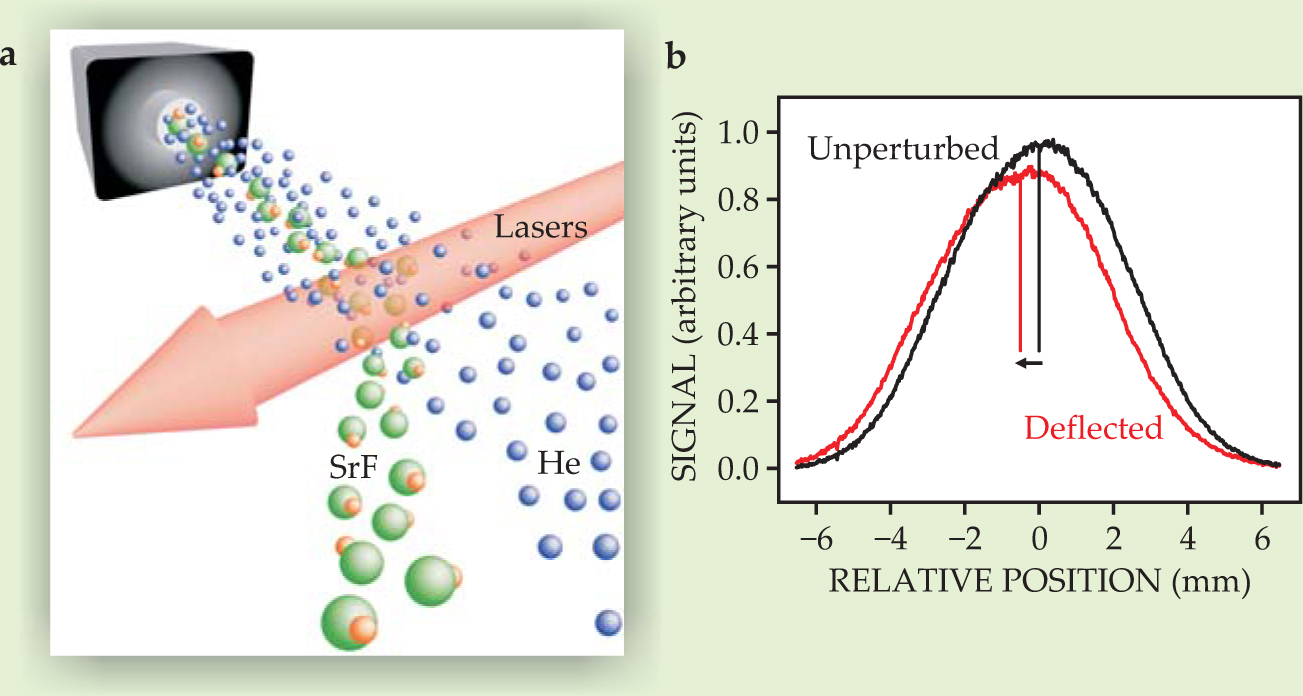
The researchers tested their scheme by irradiating a SrF molecular beam (cooled to 4 K with a buffer gas of helium) from one side, as shown in figure 2(a). By measuring the light produced when the molecules reemitted their absorbed photons, they estimated that each SrF molecule undergoes about 150 cycles. That estimate was confirmed by the deflection of the molecular beam, as shown in figure 2(b). The number of cycles was limited not by the molecules getting stuck in dark states but by the time they took to pass through the laser beams. Modifying the experimental setup to increase that interaction time would thus increase the number of cycles. Adding a third laser, as shown in figure 1, to excite molecules from the ground state’s ν = 2 vibrational level would increase it further.

Hidden gems

From the one-sided irradiation of a molecular beam, it is straightforward to irradiate the beam from all four sides. So-called transverse cooling—focusing the beam by controlling its radial spread—is a useful achievement in its own right, with applications to numerous molecular-beam experiments. Creating a stationary cloud of ultracold SrF molecules will require the additional steps of slowing the beam, trapping the molecules, and cooling them in all three dimensions. But 3D cooling would be complicated by the fact that the magnetic field that splits the Zeeman levels can’t be at the optimal angle to all the laser beams simultaneously. The Zeeman levels can also be remixed with Ye and company’s pulsed electric field, a microwave field, or rapid switching of the laser polarization. Says DeMille, “Those methods are somewhat more experimentally involved but do not seem to present any serious obstacles.”

The Yale group’s optical-cycling scheme is limited in applicability to molecules with nearly diagonal Franck–Condon arrays, but such molecules are perhaps not as rare as one might expect. DeMille estimates that there are about a dozen diatomic molecules sufficiently similar to SrF and another dozen like the TiO of Ye and colleagues’ proposal. And there may be even more hidden gems among molecules whose spectroscopic data haven’t been cataloged yet—for example, an as-yet-undiscovered metastable state might play the role of the ground state in a cycling scheme. As Di Rosa puts it, “Molecules with suitable cycling transitions may be a relative rarity but are not few, owing to the sheer numbers from which we draw.”