New angles to refraction and reflection in chiral liquids

Augustin-Jean Fresnel predicted in 1822 that a light beam would split into two beams as it enters a chiral liquid—that is, one containing molecules that lack mirror symmetry. The splitting in a chiral liquid occurs because right-handed circularly polarized light and left-handed circularly polarized light travel at different speeds and hence see different indexes of refraction. Fresnel proposed an experiment to measure the angular splitting in a chiral solution, but the angle of splitting, on the order of microradians, is too small for Fresnel to have detected it. He did, however, observe the double image produced by light that had traversed a quartz crystal, which is birefringent because of its anisotropy. He used the effect to prove the existence of circularly polarized light.

Recently, Ambarish Ghosh and Peer Fischer of the Rowland Institute at Harvard University used a scheme similar to Fresnel’s to measure the tiny angle of splitting between the two directions of polarization in a chiral liquid. Fischer said they were surprised that no one seems to have measured this angle before them. Perhaps, he thought, that’s because previous research had focused on phase differences rather than beam positions.

One easily observable consequence of the accumulated phase difference between the two circularly polarized components is the rotation of polarization of plane-polarized light. Plane-polarized light is a coherent superposition of equal contributions of right- and left-handed circularly polarized light. Because one of the components travels more slowly than the other in a chiral liquid, a phase difference develops, causing the polarization vector of the superposition to rotate.

Researchers today routinely use optical rotation to measure the concentration or the handedness of chiral molecules in solution. Much of organic stereochemistry is concerned with chiral molecules. Most drugs are chiral and are now marketed as single enantiomers—that is, molecules with the same chirality—because the mirror image can have a different effect on the human body.

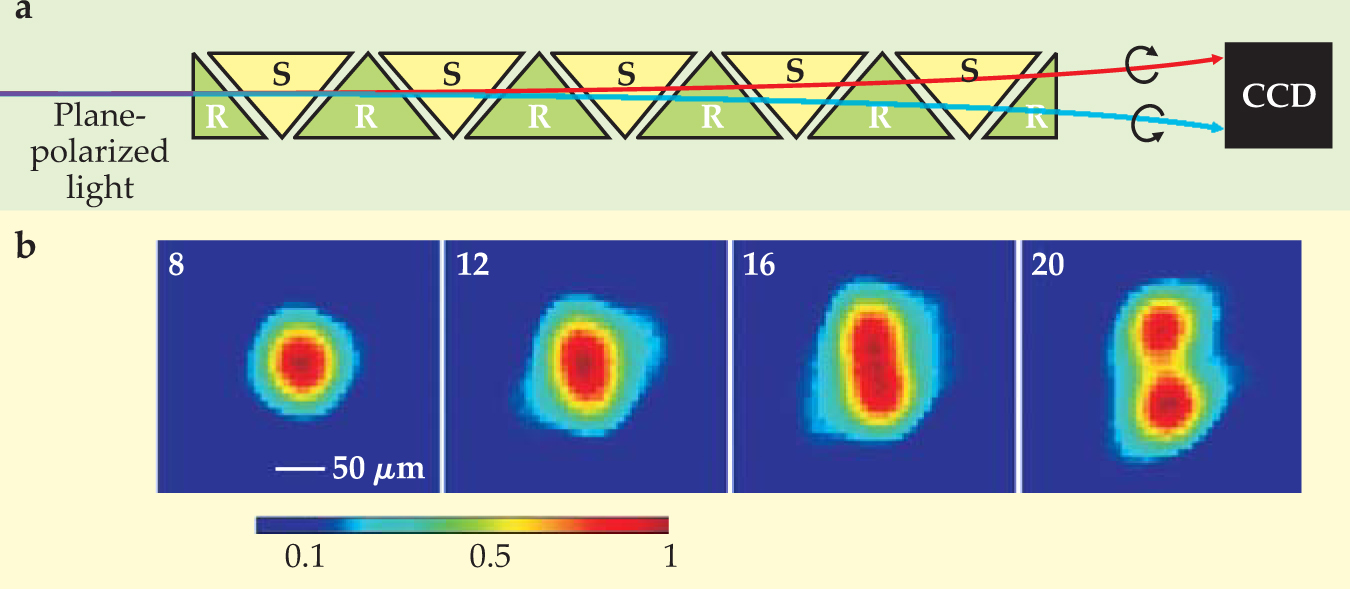
To image the angular splitting, Ghosh and Fischer sent a plane-polarized light beam through a series of prismatic containers (cuvettes) filled in an alternating pattern with left-handed and right-handed enantiomers (see panel a of the figure). Because the angles at which the rays enter and leave a cuvette change along with the type of enantiomer filling that cuvette, the component rays diverge further at each interface. Panel b shows the image of the beams on a CCD camera after the light has traversed 8, 12, 16, and 20 angled interfaces, respectively.

Ghosh and Fischer used the multiple cuvettes shown in the figure to increase the spread of the refracted rays enough for the separate beams to be seen with a CCD camera. But the experimenters were also able to measure splitting that occurs at a single interface using a position-sensitive detector, which recorded the tiny movement of a laser beam after it had traversed the interface. Simultaneous modulation of the laser beam’s polarization between right- and left-handed circular light permitted the detection of beam movements as small as 10 nanoradians.

With such a detector, the experimenters determined the angle of reflection of light that bounced off a single interface from within a chiral liquid. Contrary to the lesson taught in school, the angle of incidence in this case is not equal to the angle of reflection. No great principle is being violated. The experimenters explain that the handedness of the circularly polarized light changes upon reflection, so that the reflected light sees a different refractive index n than the incident light. From the boundary conditions on the electromagnetic waves at the interface, one arrives at a requirement equating the tangential components of the incident and reflected wavevectors, k _i and k _r. Thus, the condition k _i sin θ_i = k _r sin θ_r governs the reflection.

The splitting at a single surface is a measure of the sample’s circular birefringence—that is, the difference in refractive index seen by the two circularly polarized beams. Ghosh and Fischer found that the circular birefringence measured by the angular splitting is consistent with that determined by conventional optical-rotation measurements. Thus, they note, the two techniques yield equivalent information. In optical rotation, however, the magnitude of the rotation of the polarization vector is proportional to the distance traveled through the sample. By contrast, angular splitting is determined at the surface and is independent of the sample thickness. The angular splitting technique thus might hold promise for use with very small samples, such as are required in microfluidics or thin films.