Jamming connects granulation and flow

Cake recipes typically instruct bakers to add wet ingredients to a powdery flour mixture. Adding just the right amount of moisture is critical to making batter: Too little liquid results in dry clumps, whereas too much produces a watery mess. But just the right amount makes a smooth, flowing batter.

Incorporating liquids into powders is also common in industrial materials processing. The applications typically fall in different parts of the wetness spectrum: Production of powdered laundry detergent, for example, employs so-called wet granulation—a small amount of added liquid binds microscopic particles in small clumps, or granules. In the mixing of cement, on the other hand, the desired product is a high-solid-content dispersion that can be poured.

Those processes are more complicated than just mixing components in the right ratios. Inactive ingredients might be added to achieve certain properties. Protocol matters too: Changing how the components are added and how they get mixed together can significantly alter the final product. And for large-scale processes, those factors can all affect the amount of energy needed to do the mixing.

With so many variables to tune, researchers face a daunting task when it comes to optimizing a mixing process. They typically focus on the small region of parameter space around their desired product. Now Daniel Hodgson and Wilson Poon at the University of Edinburgh in the UK and their collaborators provide a broader view. ¹ The results of their experiments, which span the fluid-to-granulation transition, point to frictional jamming as the primary mechanism behind granulation. They also suggest that simple rheological measurements can be sufficient to predict granule properties.

A sticky situation

Although experiments on dense suspensions and granulated materials have largely focused on either freely flowing or fully granulated materials, theorists have been working to develop a single physical picture that links the two phases. ² After all, both are achieved by mixing the same kinds of components—liquids and powders—just under different conditions. Granules form when the dispersed particles become jammed, meaning they’re stuck in a disordered configuration and can’t rearrange. (See the Quick Study by Jasna Brujic, Physics Today, November 2010, page 64 .) But why, and under what conditions, do dispersed particles become jammed?

The friction-driven jamming picture arose as part of a change in how the rheology community understood why particulate suspensions undergo shear thickening—an increase in viscosity with increased applied stress. Shear thickening had been attributed to groups of particles being forced by the surrounding flow to move together as a whole. Now it’s understood to arise from forcing particles into frictional contact with a sufficiently high applied stress that prevents them from sliding past each other.

One promising explanation for the onset of granulation involves the same underlying physics. If interparticle contacts are lubricated by a thin layer of liquid, a liquid–powder mixture should be able to flow as long as the solid-volume fraction ϕ remains below the random-close-packing value ϕ_RCP—the maximum volume fraction achievable by filling a space with randomly packed objects, which is about 64% for uniformly sized spheres. If the interparticle contacts are unlubricated, though, static friction between particles further impedes flow. Mixtures would then become solid at some ϕ < ϕ_RCP.

But the connection between frictional interparticle contacts and granulation remained speculative. A proposed picture in which history-dependent flows affect a suspension’s route to granulation, for example, was still plausible. ³ And experimental evidence one way or the other was lacking. “If you look in the literature, dense-suspension rheology and granulation are totally separate fields,” says Hodgson. “They are nearly never tackled in the same work or the same way.”

To flow or not to flow

Filling in that knowledge gap was the goal of Hodgson’s PhD research. For the powder in their experiments, Hodgson and coworkers chose glass spheres with an average diameter of 10 µm. The polydisperse particles more closely mimicked the materials used in industrial settings, and since they were cheaper than the monodisperse ones often used in colloidal experiments, the researchers could produce larger-volume samples. Glycerol was chosen as the liquid because its high density and viscosity prevented noticeable sedimentation in fluid samples for the few hours each experiment lasted.

Figure 1a illustrates how volume fraction and mixing stress affected the final material. The liquid and solid components in each sample first underwent high-stress mixing (top row) and then subsequent low-stress mixing (bottom row). Three regimes emerged: At ϕ = 0.55 and below, the suspensions flowed; at ϕ = 0.70 and above, permanent granules formed. Intermediate volume fractions produced large granules after high-stress mixing, but the granules were transient—they relaxed into fluids following low-stress mixing.

Figure 1.

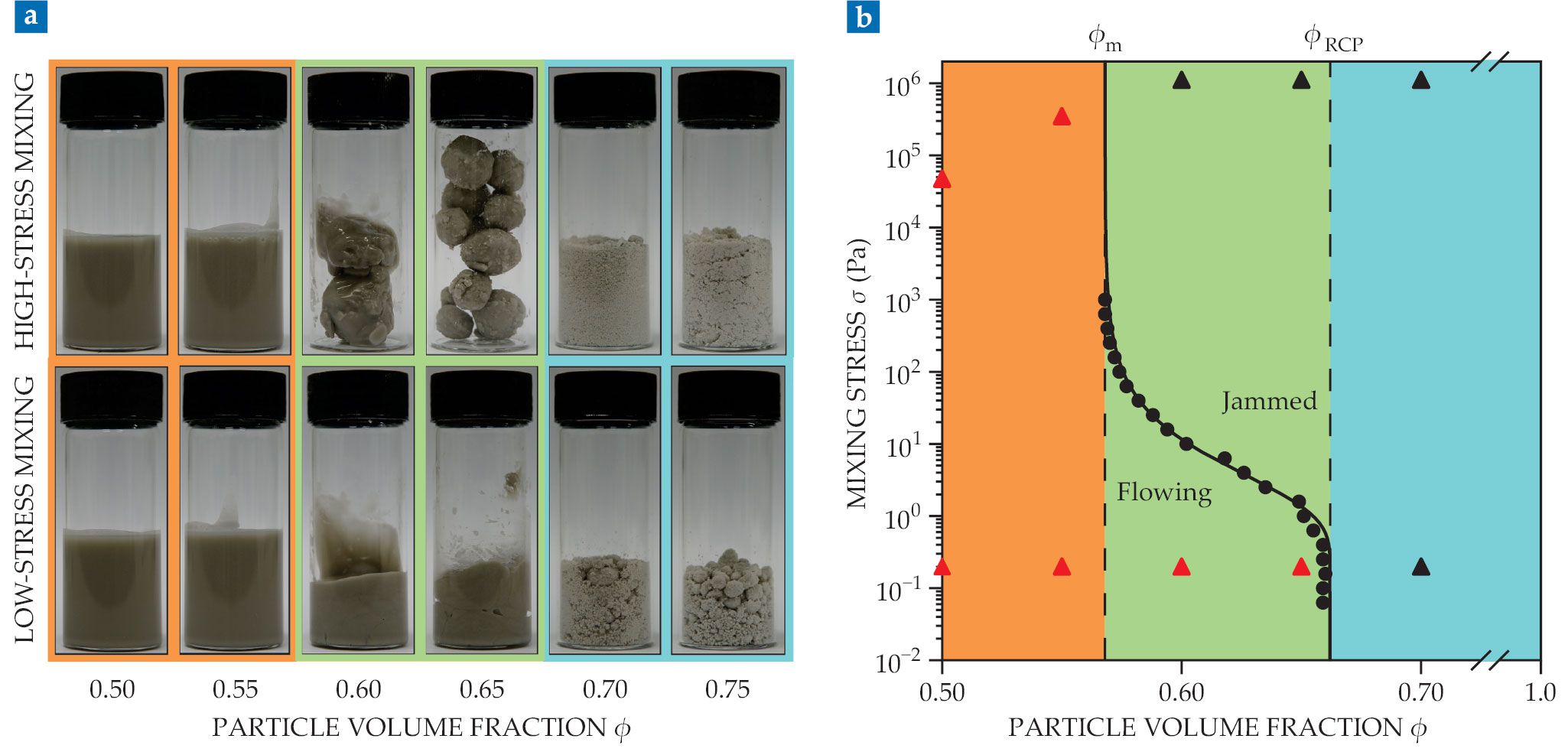
To understand the physical origins of the three regimes, the researchers turned to steady-state flow measurements: They subjected the fluid samples to a constant stress and measured the viscosities. The suspensions thickened under stress, as expected, and the viscosity diverged at some value ϕ_J; above that value, the samples no longer flowed. Where the viscosity diverged depended on the stress.

Using their measurements of ϕ_J(σ), shown as black dots in figure 1b, the researchers constructed a phase diagram for the suspensions. At the lowest stresses, suspensions flowed for volume fractions up to ϕ_RCP = 0.662, consistent with lubricated interparticle contacts. Samples with higher volume fractions were always granulated. With increasing stress, the volume fraction at which flow stopped fell until it reached a minimum value of ϕ_m = 0.568. Below that value, samples were always fluidlike. Between ϕ_RCP and ϕ_m, whether a sample was solid or fluid depended on the stress. The samples in figure 1a (represented as triangles in figure 1b) fell neatly into the appropriate regions of the phase diagram.

“Crucially, Hodgson and coworkers show experimentally that there is indeed a mapping between granulation behavior and steady-state flow behavior,” says Mike Cates, a professor of mathematics at the University of Cambridge. A direct connection between steady-state flow measurements and granulation would not be possible if history-dependent hydrodynamics were involved. Additionally, says Cates, “the results further confirm the key role of interparticle friction rather than any of several alternative explanations that have been proposed to explain the wider scenario of shear thickening.”

A peek inside

Hodgson and coworkers used mass conservation to tease out the structures of the clumps formed in the granulated samples. For a given stress σ, the maximum amount of powder that can be trapped in the liquid phase is set by ϕ_J; any remaining particulate must be left behind in a separate dry phase.

But no loose powder was present in the granulated samples, so Hodgson cut some of the granules open to look inside. “The granules you end up with are very brittle,” he notes. “I had to do it many, many times to even get the small number of images we did get.” In those few images, he saw wet, jammed cores surrounded by dry particulate shells (see figure 2a). X-ray tomography measurements confirmed the general structure.

Figure 2.

From that insight about the granules’ structure, Hodgson and coworkers wrote down a formula for a sample’s average granule radius R as a function of ϕ, σ, and the shell thickness t_s (see figure 2b). The predictions for R in both low- and high-stress conditions agreed with their observations.

The formula also predicted when the granules should come together and make a flowing suspension. Those particle fractions—ϕ = 0.55 and 0.66 for high- and low-stress mixing, respectively—are the same ones at which the steady-state flow data predicted the transition between flow and granulation.

With so few images of granule cross sections, the researchers had to leave t_s as a fitting parameter in their formula. That approach yielded different parameters for high- and low-stress mixing, which may indicate another structural difference caused by the protocols. But that’s still speculation. A better understanding of what determines t_s is needed so its value can be calculated or measured—hopefully as easily as ϕ_J, which can be gathered through straightforward rheological measurements. That capability will likely be important for predicting what size granules an industrial mixing protocol will produce.

Other factors may further complicate predictions. How liquid is added to a powder, for example, can affect granule structure: Introducing it as an aerosol rather than large droplets could link particles with small capillary bridges instead of trapping them in a jammed liquid–particle core. And if interparticle interactions aren’t purely repulsive, qualitatively different properties could emerge in both the fluid and granulated states.

In a collaboration that included industry partners at Mars Chocolate, the authors of the paper observed that reducing friction shifts the onset of granulation in chocolate conching—the mixing of powdered cocoa, sugar, and milk with cocoa butter to produce chocolate’s distinctive texture. ⁴ And, notes Hodgson, “because we’re dealing with the underlying fundamental physics, we’re not sector specific.” The same underlying physics and phenomenology should also apply to concrete production, for example. And since surfactants used in many systems to reduce friction are derived from petrochemicals, adjusting friction can also be an opportunity to move to a more environmentally sustainable formulation.