Holograms tie optical vortices in knots

What’s the physical significance of a knot? William Thomson (who later became Lord Kelvin) must have asked himself that question in 1867 when he proposed his “vortex atom” hypothesis—the idea that different knotted configurations of swirling vortex lines in the ether are manifest in nature as different atoms. Earlier that year he’d witnessed Peter Guthrie Tait’s intriguing experiments on smoke rings. And based on earlier work by Hermann von Helmholtz, he knew that lines of vorticity are topologically conserved quantities. The closed loop and knotted configurations Thomson envisioned would thus be discrete and immutable—ideal traits for a theory of atoms.

Although initially skeptical, Tait came to believe that one could account for the rich variety of atoms in the periodic table by systematically building a classification system for all types of knots. For the catalog he produced, Tait is now viewed as the father of knot theory. Thomson, for his part, had to abandon the vortex atom hypothesis. Ironically, though, it wasn’t due to the nonexistence of the luminiferous ether—the 19th century’s perfect fluid—but to an inability to analytically prove the temporal stability of a vortex knot. Still, the subsequent history of physics is filled with examples of systems—among them cold turbulent superfluids, hot magnetized plasmas, and cosmic strings in the evolving universe—in which the knottedness of vortex lines is thought to play a prominent role. In their efforts over the past few years to quantify and understand the shared topological properties of such disparate systems, Mark Dennis (University of Bristol), Miles Padgett (University of Glasgow), and their UK colleagues have been exploring the topology of yet another system: a beam of light. The researchers have now demonstrated, using a sophisticated holographic-grating scheme, that the dark threads in a complex optical field can be shaped into loops, linked loops, and knots of arbitrary topology. ¹ The trick lay in finding the exotic solutions to Maxwell’s equations—or, more precisely, the paraxial wave equation—that do the job.

Speckle patterns

The physics of scattered waves underlies the achievement. When three or more optical waves interfere in space, complete destructive interference occurs along nodal lines. At those places, known as optical vortices or phase singularities, the light intensity is zero and the phase undefined. Circling them, the phase increases or decreases by 2π.

In a three-dimensional light field—such as laser speckle, observed when coherent light scatters from a rough surface—the nodal lines can form the sort of complicated tangle shown in figure 1. The numerical simulations of speckle patterns that Padgett, his graduate student Kevin O’Holleran, and Dennis made by superposing random plane waves reveal a complex electromagnetic field marked by a network of continuous and looped optical vortices that thread the entire volume of the light field.

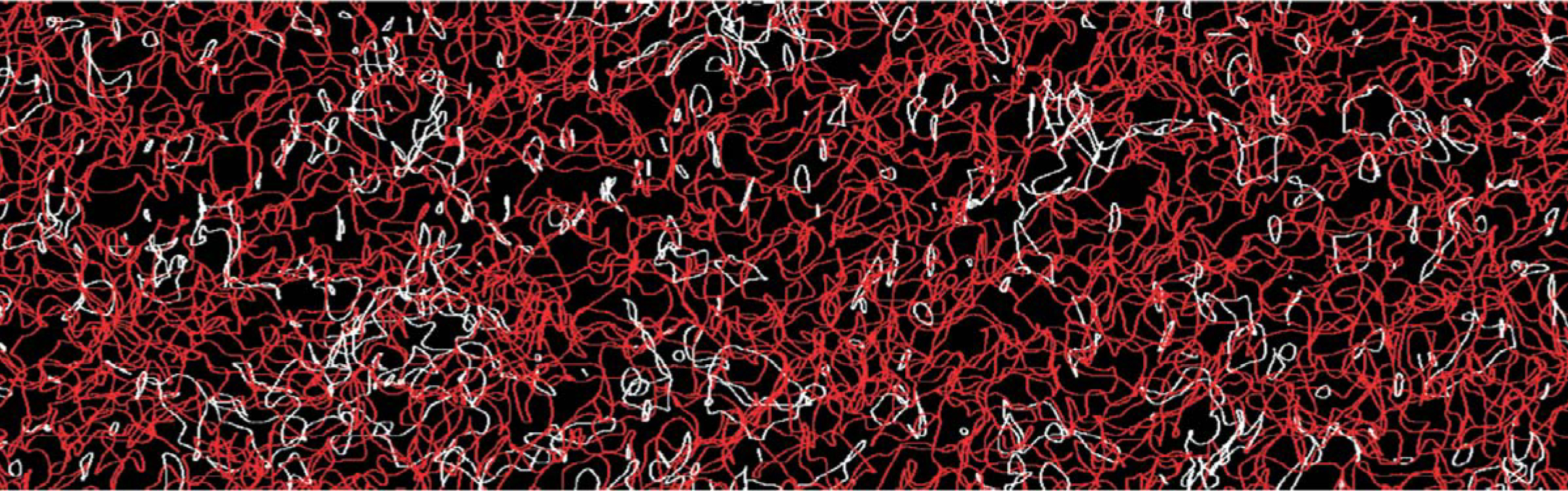
From the simulation data, the researchers mapped the distribution of topological features and identified vortex loops that were threaded or unthreaded by vortex lines and loops that were linked with other loops. Not surprisingly, larger loops were more likely to be linked or threaded than smaller loops. ² Earlier experiments in which a frosted glass screen was placed in front of a helium-neon laser beam bore similar results. ³ Although links between two loops were found occasionally, no knots appeared in either real laser speckle or the simulations of random superpositions, probably because the chance of their formation is so low.

Designer knots

In 2001, well before the speckle studies, Dennis and his then thesis adviser Michael Berry predicted that vortex knots—or “knotted nothings,” as they dubbed them—could be artificially manufactured using the superposition of a few laser beams with properly designed intensities and phases. The trouble with an early prescription they conceived was that the knots it created would be inextricably connected to infinitely long vortex lines and loops in the system. The theoretical challenge was thus to construct a solution to the time-independent paraxial wave equation—the small-angle limit of the general wave equation—that specifies a scalar field containing nothing but the desired knot. The experimental challenge, in turn, was to imprint that solution onto an actual light wave.

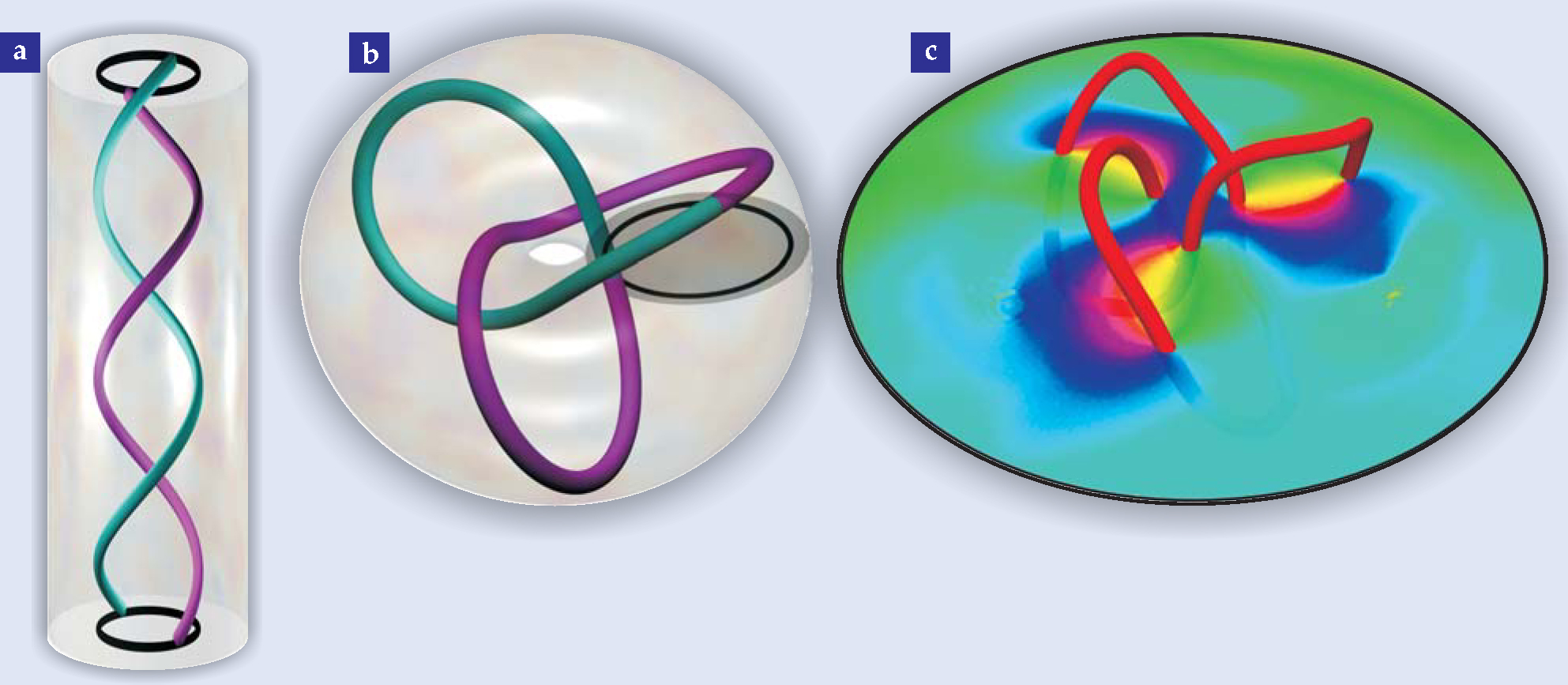
Wrestling with the theoretical issues last year, Dennis and his student Robert King experienced a revelation. The pair realized they could exploit a mathematical operation known as Milnor mapping, which transforms a complex-valued scalar function that’s simple to construct but doesn’t contain a knot into a more complicated function that does. Figure 2 outlines the idea. To build a trefoil knot, for instance, they devised a function that describes a periodic braid—two nodal lines that spiral around each other up or down a cylinder. Under Milnor mapping, the top and bottom of the cylinder bend around to meet each other, so that the braid’s two lines are spliced into a single knotted loop residing in a torus.

The lines cross three times in a trefoil knot, but more complicated topologies readily emerge by increasing the lines’ crossing number or altering the trajectory they take—from circular to figure-8, say—as they’re braided. The technique is powerful: In 1923 topologist James Waddell Alexander proved that braiding yields every type of knot.

To experimentally create the scalar “knot” field, Padgett, along with students O’Holleran and Barry Jack, used a diffractive hologram as a spatial light modulator. The hologram, essentially a computer-controlled liquid-crystal film, generates the appropriate interference pattern, pixel by pixel, across an incoming laser beam’s profile. The light propagating from the hologram then has a phase pattern determined by the shape of its grating lines and an intensity determined by their contrast.

Typically, the dynamic range of intensity in the theoretically calculated knot cannot be achieved experimentally because of technical limitations of the hologram. So an iterative procedure that incrementally lowers the required contrast while preserving the knot was devised to optimize the hologram’s design.

Figure 2(c) shows the experimental trefoil knot, made evident by mapping the optical field’s phase distribution. In practice, the Glasgow team interferometrically measured the various phases, represented by different colors, across about 100 cross sections of the beam. The phase singularities, points where the colors meet in each cross section, were then stitched together into lines that make up the knot.

Other waves, other knots

As linear solutions to a time-independent wave equation in free space, the vortex-knot patterns are stable and static. But there also exist exotic time-dependent solutions of Maxwell’s equations that describe knotted structures. Two years ago physicists William Irvine (New York University) and Dirk Bouwmeester (University of California, Santa Barbara) studied solutions, based on a topological construction known as a Hopf fibration, in which all electric and magnetic field lines are closed loops and any two electric or magnetic field lines can be linked and knotted. ⁴

Because they’re scalar, vortices are relatively easy to manipulate using holograms. In contrast, Irvine and Bouwmeester’s field-line solutions have the vector character of the electric and magnetic fields built into them, presenting the experimental challenge of dynamically measuring their vectors in 3D space.

Knot theory has already influenced particular areas of physics—most notably topological quantum computing (see the article by Sankar Das Sarma, Michael Freedman, and Chetan Nayak in Physics Today, July 2006, page 32 .)

The exquisite control that researchers can now exert to knot optical fields may catalyze other applications. The light around optical vortices has orbital angular momentum and thus can exert a torque, which has been widely exploited in ringlike optical traps, for example (see the article by Padgett, Johannes Courtial, and Les Allen in Physics Today, May 2004, page 35 .) Padgett speculates that the rarity and sensitivity of optical knots within scattered light may even form the basis for a new kind of molecular sensor.

Applications aside, Irvine finds them fascinating examples of the close connection between geometry and Maxwell’s equations. “I can’t say whether knots tied in fields are important physical objects or not,” he says. “It probably depends on what exactly is tied up. But for me, they’re curious, beautiful, and hard to resist.”