Graphene reveals the Hall-mark of strongly interacting electrons

Researchers have long been fascinated with two-dimensional systems, in which electrons often obey different rules from those that apply in the bulk. For decades, scientists have exploited the surprising and useful phenomena exhibited by electrons that form an effectively 2D gas at the interfaces between layered semiconductors.

Graphene, a single plane of carbon atoms in a hexagonal lattice, comes closer to the 2D ideal than do the semiconductor electron gases. Moreover, graphene has unique electronic properties that researchers are eager to measure. That’s why those in the field were so excited in 2004 by the demonstration of a technique to isolate and study what is essentially the top sheet of the layered carbon compound, graphite. (See the article by Andrey Geim and Allan MacDonald in Physics Today, August 2007, page 35 .)

Alas, comments Geim, “While other areas of graphene research have emerged and developed, quantum transport measurements have remained in more or less the same state as they were around 2005 or 2006.” In particular, many researchers have been frustrated by the failure of experiments to detect the fractional quantum Hall effect (FQHE), which would be evidence that electrons are forming a collective state that has a fractional electric charge. Theorists have waited for such proof of strong electron interactions to justify their hopes that intriguing new physics might follow.

Speaking at conferences in Italy and in South Korea last summer, Eva Andrei of Rutgers University surprised her audiences with evidence for the long-awaited plateau in the transverse conductance ¹ at $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.$ of the conductance quantum e ²/h. Like other groups pursuing the same goal, Andrei and her colleagues had suspended the graphene sample between two supports: Electrons in such suspended samples have far higher mobilities than those in samples resting on a substrate. In addition, the Rutgers group measured the Hall effect with a two-probe method to circumvent the challenges of applying the conventional four-probe technique to the small suspended samples.

Philip Kim and his group at Columbia University have used similar techniques to find the fractional $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.$ quantum Hall state in graphene, along with hints of plateaus at other fractional values of the conductance quantum. ² In addition, both the Rutgers and Columbia experiments shed additional light on a collective effect unique to graphene—the possible transition to an insulating state caused by symmetry-breaking electron interactions.

Relativistic Dirac electrons

The excitement over graphene’s electrical properties stems from the peculiar nature of the energy bands near a few points in momentum space. At those points, known as Dirac points, the conductance band just touches the valence band, and the energy varies linearly with momentum. The dispersion relation, when plotted, looks like an inverted cone (the conductance band) balanced on the vertex of a second upright cone (the valence band). That linear dispersion relation is the same one implied by Paul Dirac’s relativistic wave equation in the limit of vanishing particle mass. Thus, charge carriers at graphene’s Dirac points have zero effective mass and move at a constant speed, although not as fast as light.

Theorists fully expect graphene’s electrons to be strongly interacting and hence to exhibit the FQHE. The classical Hall effect appears when a current flows in a plane perpendicular to an applied magnetic field. Lorentz forces push the conducting charges toward the side of the sample, where they produce a transverse voltage. Two-dimensional systems manifest the integer quantum Hall effect (IQHE): Electrons occupy discrete Landau energy levels as a result of their quantized orbits around externally imposed magnetic flux lines. That quantum behavior shows up as plateaus in the conductance measured transverse to the current flow, when plotted as a function of the density of charge carriers. As one Landau level fills up, the conductance is flat, showing no increase with carrier density until the next Landau level is nearly filled. The plateaus appear at conductance values of νe ²/h, when the filling factor ν—the ratio of the number of charges to the number of magnetic flux lines—is an integer.

In 2005, soon after the first isolation of graphene samples, experimenters found the IQHE but with some new twists, as predicted by theory. ^3,4 (See Physics Today, January 2006, page 21 .) The plateaus were not found at every integer multiple of the conductance quantum, e ²/h, but appeared only at values given by ±4(N + $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ )e ²/h, where N is the integer labeling each Landau level. The existence of plateaus at both positive and negative filling factors reflects the special symmetry between holes and electrons in graphene. The factor of four comes from a fourfold degeneracy in graphene. One factor of two is contributed by the electron’s spin; the other comes from graphene’s crystalline structure. As Amir Yacoby of Harvard University explains it, graphene’s honeycomb lattice is composed of two interpenetrating triangular lattices; the electrons can sit on either of the two sublattices.

The observed filling factor of ν = ±4(N + $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ ) also indicates that the conductance plateaus are shifted by a half integer compared with the plateaus seen in 2D electron gases in semiconductors. That shift stems from the relativistic Dirac nature of the electrons: Because there is no energy gap between electron and hole levels, graphene does not exhibit the same insulating behavior seen in semiconductors when the carrier density approaches zero.

Fractional charges

To date, no hint of the FQHE has appeared in graphene sheets sitting on substrates. The FQHE, being dependent on fragile many-body effects, requires lower temperature, higher magnetic field, and higher mobilities compared with the IQHE. Because scattering produced by the substrate’s charged defects and by impurities trapped at the interface may reduce the sought-after electron correlations, researchers have tried suspending their graphene samples between two supports. (See figure 1.) At low carrier density, the mobility in suspended graphene can exceed 200 000 cm²V⁻¹s⁻¹, more than 10 times greater than those seen in nonsuspended samples.

To make a suspended sample, one starts with a sheet of graphene supported on a doped silicon substrate but separated from it by a thin layer of insulator. Etching away the insulating layer leaves the graphene suspended above the silicon substrate. Metallic electrodes placed atop each end of the graphene are used to apply current and measure voltage. The electron density is varied by changing the substrate’s voltage.

The suspended graphene samples must be very small, on the order of a few microns long, to remain stable. Andrei thinks that the tiny dimensions are to blame for the failure to date to see the FQHE using conventional four-terminal measurements: The probes are so close that they are being shorted out, she asserts. That’s why she turned to a measurement with just two terminals, on opposite ends of the graphene sheet.

The conductance between those two terminals is a combination of the transverse Hall conductance and the longitudinal conductance, thanks to the curved trajectories of charges in a magnetic field. At a plateau, however, the longitudinal conductance goes to zero, so in that case the two-probe measurement gives an unambiguous measurement of the Hall conductance. The data there give the correct positions of the plateaus but they do not yield reliable information away from those points. To demonstrate the validity of the two-probe technique, both the Rutgers and Columbia teams showed that it reveals the same IQHE plateaus that one sees with the four-terminal method.

As seen in figure 2, the Rutgers team found that the $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.$ conductance plateau became increasingly prominent at higher magnetic fields. The Columbia group also saw hints of levels tantalizingly near filling factors of $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ and $\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.$ .

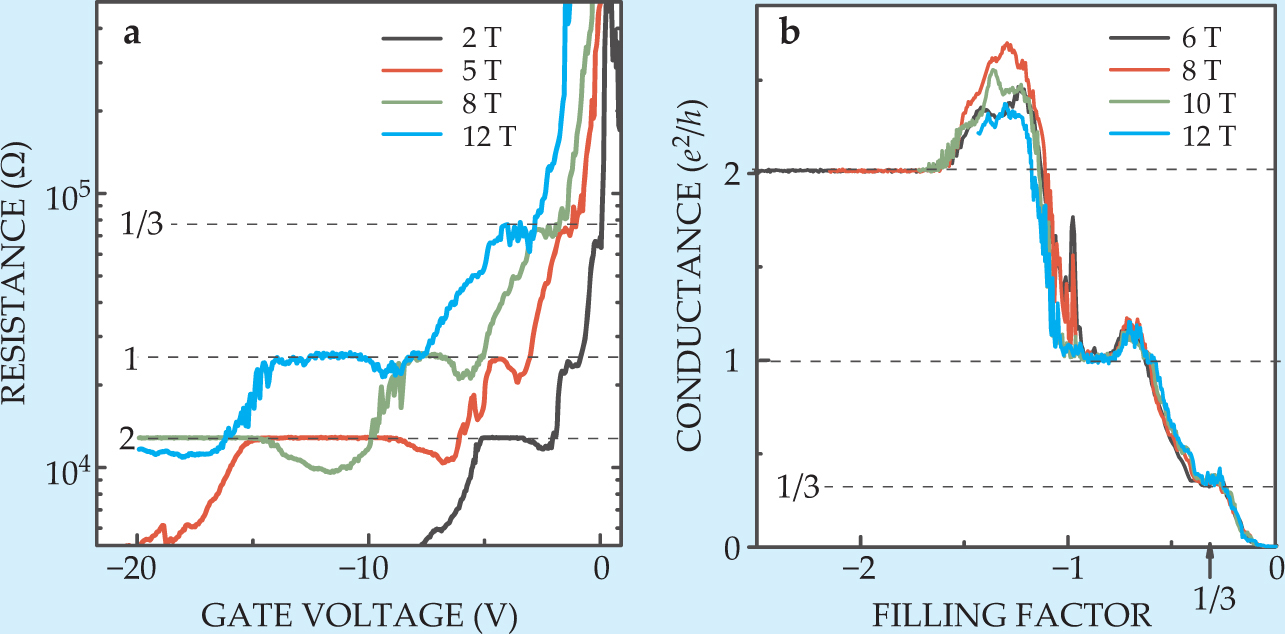
To anyone who has seen the sharp FQHE plateaus measured in 2D electron gases, the new data are not as impressive. As Kim wryly notes, they are convincing only because researchers fully expect to see the $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.$ level in graphene, as they do in semiconductors. Experimenters will continue to seek ways to gather better data, perhaps by developing large enough suspended samples that they can get results with the four-probe methods. Only by sensing the longitudinal and transverse directions independently can one fully explore the FQHE in graphene and uncover any surprises it might hold.

Evidence for strongly interacting electrons has also been seen in measurements of the IQHE in a high magnetic field. Electrons interacting in a strong enough magnetic field can break the fourfold degeneracy seen in the sequence of conductance plateaus in graphene’s IQHE. When the degeneracy is broken above a certain field strength, plateaus appear ⁵ at filling factors ν of 0, ±1, and ±4, values not allowed by the ±4(N + $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ ) formula imposed by symmetry. In graphene bilayers, the second sheet adds another degree of freedom, which results in an eightfold degeneracy at the Dirac point. Using suspended bilayers, Yacoby and coworkers found previously unseen Hall plateaus, thanks to the breaking of the bilayer symmetries in high fields. ⁶

Hints of new physics

Theorists want to learn more about the zero-energy Landau level. That level corresponds to the Dirac point, the point in momentum space where electrons behave like massless Dirac fermions. There should be no charge carriers at that point but, nevertheless, the conductance there is nonzero. As Andrei explains, one can shoot in an electron and it will go through the graphene.

What happens to the conductance at the Dirac point when a magnetic field is applied? Will graphene remain metallic, or will it transition to an insulating state? Experiments have not provided a clear answer. Measurements by a Manchester team support theories of a conducting state ⁷ but later experiments by a Princeton group show evidence for a field-induced transition to an insulating state. ⁸ According to theory, which picture prevails depends on which symmetry is broken first. In one scenario, the Coulomb interactions in the presence of a strong enough field break the sublattice degeneracy, and the Dirac point transitions to an insulating state. In another scenario, the interactions break the spin degeneracy, and the state remains conducting. In the latter case, the material is insulating in the bulk; any conductance occurs in counterpropagating edge states. Even more possibilities exist in graphene bilayers because of the greater degree of degeneracy.

The new experiments on suspended graphene have weighed in on the side of the insulating state. Both saw resistances jumping to values of 1–10 GΩ above certain critical values of the magnetic field. The critical field was as low as a few teslas, depending on the sample. Measurements on graphene bilayers also find an insulating transition, at an even lower critical field. ⁶

Both Kim and Andrei find evidence that the insulating state near ν = 0 can obscure the FQHE that appears not far away at ν = $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.$ . N. Phuan Ong of Princeton University thinks that the competition between those two effects will be one of the interesting questions to explore in future experiments.