Elementary excitations in spin ice take the form of magnetic monopoles

Ferromagnetism —the ability of materials such as iron to form permanent magnets—arises from the spontaneous alignment of atomic spins when atoms interact with each other. But some magnetic solids, especially ones that are geometrically frustrated, exhibit rich and complex effects of those interactions. The behavior of a solid depends not just on the positions of its atoms but also on their local properties—the electric, magnetic, or rotational degrees of freedom. So when the energetically preferred alignment of magnetic moments in a lattice is incompatible with the underlying crystal geometry, exotic phases can emerge (see the article by Roderich Moessner and Art Ramirez in Physics Today, February 2006, page 24).

One of those phases, spin ice, is a strange magnetic state in a material whose ions reside on the vertices of the pyrochlore lattice, a network of corner-sharing tetrahedra. A strong crystal field produced by the local environment of the ion favors an arrangement in which spins point either into or out of the centers of each tetrahedron. But as the temperature falls, geometric frustration inhibits the formation of a simple, ordered spin configuration in which every bond connects an in–out pair.

To minimize the energy, the best compromise is one in which two spins point into and two point out of each tetrahedron. That simple organizing principle, called an ice rule by analogy to the way hydrogen atoms are positioned around a central oxygen atom in water ice, can be satisfied by an exponentially large number of energetically equivalent arrangements of spins. The huge set of degenerate ground states is responsible for a characteristic property of spin ice: Although the material is structurally ordered, it remains magnetically disordered—and thus retains a residual, zero-point entropy—even as its temperature approaches absolute zero.

Claudio Castelnovo (Oxford University), Roderich Moessner (Max Planck Institute for the Physics of Complex Systems, Dresden), and Shivaji Sondhi (Princeton University) have discovered another remarkable property of spin ice: Its localized excitations above the ground state form a new and unexplored class of solid-state defects—magnetic monopoles that can split from their parent dipole and diffuse around the crystal as free charges. ¹

In crystals at low temperature, elementary excitations often behave like particles. Solitons, phonons, and magnons, for example, are all quasi-particles that carry quantized amounts of energy, momentum, or spin and emerge from the collective interactions of many atoms. What distinguishes spin ice is that it is the first example of a three-dimensional system that behaves as if its fundamental building block, the electron spin, breaks apart—much like the electric charge does in the two-dimensional fractional quantum Hall effect (see reference and the article by Philip Anderson in Physics Today, October 1997, page 42 ). Through the subtleties of many-body physics, the spin-ice system mimics the properties of a dilute gas of magnetic monopoles.

Splitting the dipole

Spin-ice compounds are among the most densely magnetic of all substances. The magnetic dipoles are closely packed, and their dominant interactions are long-range and strongly anisotropic due to the coupling of spin and position vector components in the dipolar spin Hamiltonian. To calculate with so complex a Hamiltonian, theorists in recent years have had to rely on numerical simulation. But the complexity raises the question, Why does the simple (and local) ice rule work so well?

Researchers have long suspected that the ice rule is not a purely local effect acting among nearest-neighbor ions but rather an emergent, many-body property of the long-range interactions. ³ Castelnovo, Moessner, and Sondhi discovered the unusual excitations in spin ice using a model that accounts for the empirical observation that ice-rule states are roughly equivalent to the ground states of dipolar interactions. In essence, the researchers reframe the Hamiltonian from one based on the sum of interacting dipoles to one based on the sum of local magnetic charges, which they identify as the natural degrees of freedom at low energies.

The effective change to the Hamiltonian is slight, it turns out, and akin to a coordinate transformation that vastly simplifies the calculation. The interaction energy of each magnetic dipole living on a pyrochlore lattice site is replaced by the energy of a pair of opposite magnetic charges, one in the center of each neighboring tetrahedron. To visualize the idea, imagine the spins stretched into dumbbells, as pictured in the figure on page 16. The crucial insight is that in the ground state the four magnetic charges (two positive, two negative) in each tetrahedron cancel each other out. Long-range dipole interactions are, on average, screened out, so that the magnetic field in the system vanishes when the configuration obeys the ice rule.

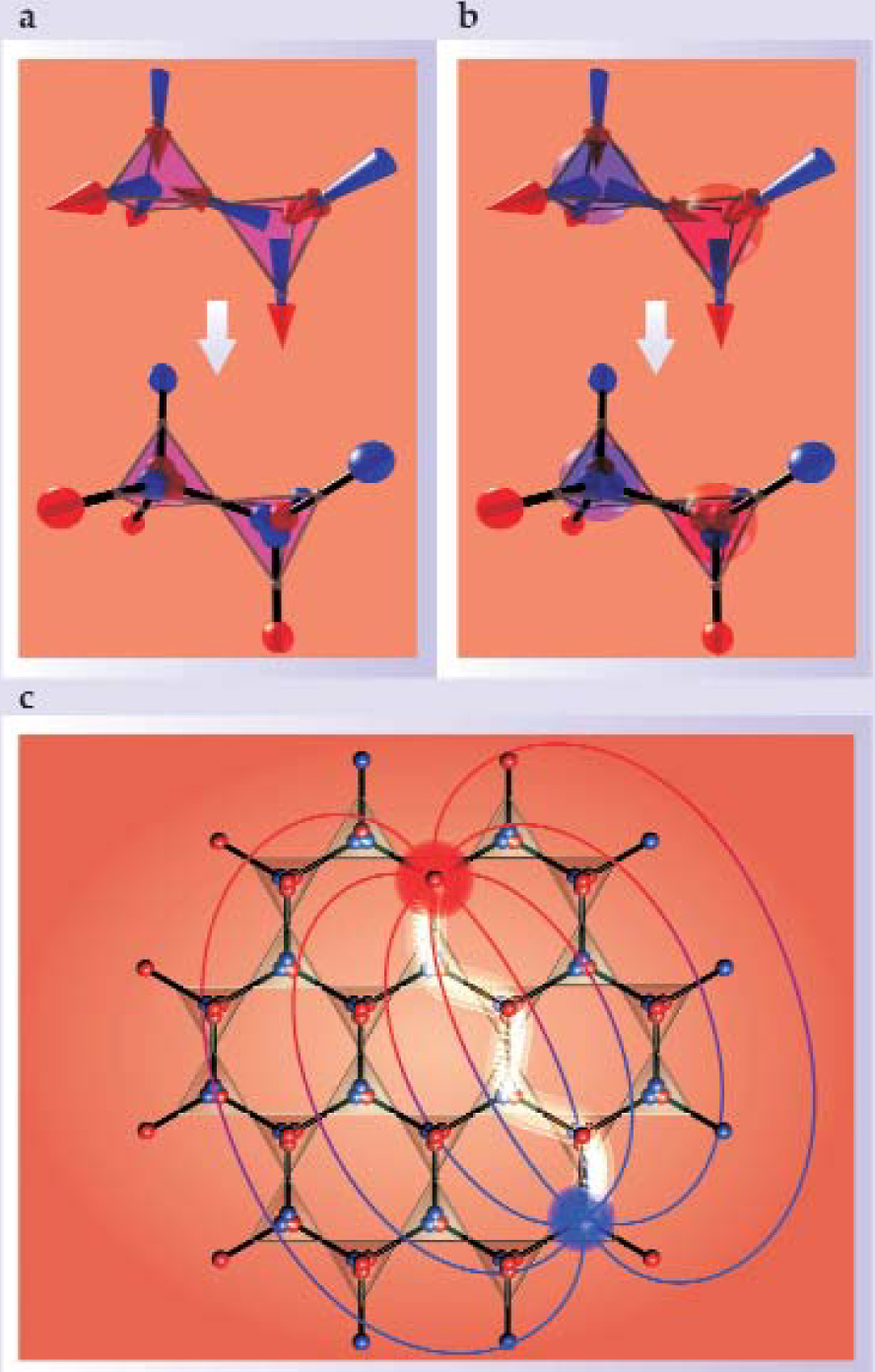
What about excited states? The most elementary excitation is the inversion of a single dipole to generate a local net dipole moment. The inversion breaks the ice rule in neighboring tetrahedra and creates two magnetic charges ±q _m, a nearest-neighbor monopole–antimonopole pair represented by the large colored balls in the figure; one monopole represents a state in which three spins point out and one in, while the other represents a state in which one spin points out and three in. The monopoles can be separated from each other without further violations to charge neutrality by flipping a chain of adjacent dumbbells. Indeed, one can envision monopoles in spin ice as magnetic analogues of electrically charged defects H₃O⁺ and OH⁻ in water ice.

Deconfined monopoles migrate independently around the bulk crystal. A pair separated by a distance r experiences a Coulombic potential −µ₀ q _m ²/(4πr), where µ₀ is the vacuum permeability. Because they are embedded in a crystal with a fluctuating magnetization M, the monopoles can act as sources and sinks of the magnetic field H while still preserving a zero divergence in the magnetic flux density B, in accord with Maxwell’s equations.

Finding monopoles

At least conceptually, detecting the presence of a monopole is straightforward. The magnetic flux measured in a superconducting quantum interference device wrapped around a wire of spin ice should change as a monopole drifts down the wire and through the SQUID. Practically, the experiment is tough. The charge on a spin-ice monopole is tiny, roughly 1/8000 the charge of an elementary Dirac monopole, so the measured change in a SQUID would be 1/8000 the flux quantum h/2e. Moreover, the monopoles must be dilute enough that just one or two of them diffuse through the SQUID at any one time. The temperature required to guarantee that is so low that other issues become more worrisome—in particular, the dynamics become very slow.

Castelnovo and colleagues take a different approach to building confidence in their theory. By applying a magnetic field along a crystallographic direction in spin ice, they argue, one can essentially tune the density of monopoles. Varying the magnetic field at different temperatures maps out the system’s phase diagram.

Five years ago, researchers observed ⁴ a line of first-order phase transitions in the spin ice dysprosium titanate below a critical temperature of about 0.36 K in an applied magnetic field around 0.9 T. How to interpret the transition has remained mysterious until now, says Moessner. By accurately reproducing the phase diagram, the new spin-ice model accounts for the transition as the condensation of a dilute gas of monopoles into a dense liquid.