Efimov trimers imaged for the first time

Something strange happens when the force of interaction between two particles is gradually weakened: Just as the last two-body bound state is on the verge of becoming unbound, an infinite series of loosely bound three-body states suddenly appears. The particle trios are held together only by the intricacies of quantum mechanics—not by covalent or ionic bonding or any of the other mechanisms that stabilize more familiar multiparticle systems. And they spend most of their time in a classically forbidden region of the potential.

Forty-five years have passed since Vitaly Efimov predicted those trimers that now bear his name. ¹ Efimov trimers eluded experimentalists until 2006, when Rudolf Grimm and colleagues at the University of Innsbruck in Austria inferred their existence in an ultracold cesium gas by monitoring the loss of atoms from an optical trap. ² (See Physics Today, April 2006, page 18 .) A spike in the loss rate showed that a three-body state formed exactly as Efimov’s theory said it would. But the Innsbruck researchers were unable to capture the cesium trimers to learn more about them.

Now Reinhard Dörner, his postdoc Maksim Kunitski (both at Goethe University Frankfurt in Germany), and their colleagues have implemented a more direct approach. Using helium rather than cesium and a molecular beam rather than a trap, they’ve managed to isolate and image trimers in the elusive Efimov state. ³

Disappearing trimers

One of the defining features of an Efimov state is that it exists only when the interparticle potential is sufficiently weak. Strengthen the interaction too much, and the trimer dissociates into a dimer and a monomer. In a trapped gas of cesium or other alkali metal atoms, the interaction, characterized by the scattering length a, can be tuned experimentally by varying an external magnetic field. But in their helium-beam experiments, Dörner and colleagues were limited to the He potential provided by nature for the noble gas. The effect of strengthening or weakening the interaction had to be deduced theoretically by computationally scaling that potential.

Figure 1 shows the results of that scaling. When a > 0, a two-body bound state exists; when a < 0, it doesn’t; and at the threshold between the two regimes, a diverges.

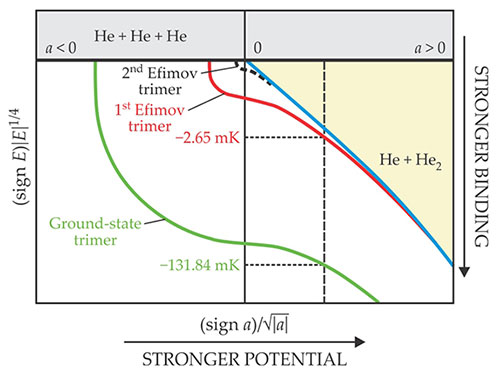
Stable three-body bound states can exist only below the blue curve, which represents the He dimer’s binding energy. Efimov states (of which only the first two are shown) all intersect that curve: As the interaction is strengthened, they disappear one by one. But the ground-state trimer—an ordinary van der Waals cluster, not an Efimov state—never vanishes, no matter how strong the interaction.

For real He, a is about 90 Å. Its bound states, as shown by the vertical dashed line, include the dimer, ground-state trimer, and first Efimov trimer. All of them are so weakly held together that their binding energies are best expressed in millikelvin. (In contrast, the binding energy for molecular hydrogen is 50 000 K.) That’s far too feeble to withstand the usual tools of molecular identification, mass spectrometry and rotational–vibrational spectroscopy. A new suite of methods was required.

Coulomb explosion

Most of the atoms in a He molecular beam exist as unbound monomers, with only a few combining into dimers, trimers, tetramers, and larger clusters. In 1994, J. Peter Toennies and Wieland Schöllkopf devised a way to sort such fragile clusters using matter-wave diffraction. ⁴ Just as optical diffraction gratings separate light by wavelength, matter-wave diffraction gratings separate particles by their de Broglie wavelength. In a cryogenic beam, He atoms have a de Broglie wavelength of a few angstroms, so a grating with periodicity 100 nm deflects them by a few milliradians. Dimers are deflected by half as much; trimers by a third.

With their diffraction experiments, Toennies and Schöllkopf produced some of the first experimental evidence that He dimers and trimers exist. But the question remained of how to separate ground-state and Efimov trimers, which have the same mass. Theory showed the Efimov trimer to be an order of magnitude larger than the ground state. But attempts in the early 2000s to diffract the trimers in a way that’s sensitive to both mass and size were unsuccessful. ⁵

Meanwhile, Dörner and his group were using a technique called cold-target recoil-ion momentum spectroscopy, or COLTRIMS, to study molecular structures and fragmentation processes. ⁶ In one implementation of the technique, called Coulomb- explosion imaging, a short, intense laser pulse simultaneously ionizes every atom in a molecule. As the ions fly apart under the force of Coulomb repulsion, an electric field guides them to a detector. From the position and time at which each ion strikes the detector, one can reconstruct the momentum imparted to it in the explosion and, from that, the molecular structure.

Dörner realized that Coulomb- explosion imaging offered a way to distinguish Efimov and ground-state trimers. But building a dedicated machine optimized for Efimov study was an expensive and risky proposition. “There was a big chance that we would fail,” he says. “Theory predicted that the Efimov state was stable, but it was totally unclear how to make it and how much could be produced.” If too few of the trimers were in the Efimov state, their signal would be overwhelmed by background and by the ground state, despite the experimenters’ best efforts.

In 2008 the German Research Foundation introduced a new grant program, the Reinhart Koselleck Projects, to provide long-term funding for “exceptionally innovative or higher-risk projects.” Dörner sought and received a Koselleck grant in 2009, and his team got to work developing the apparatus sketched in figure 2.

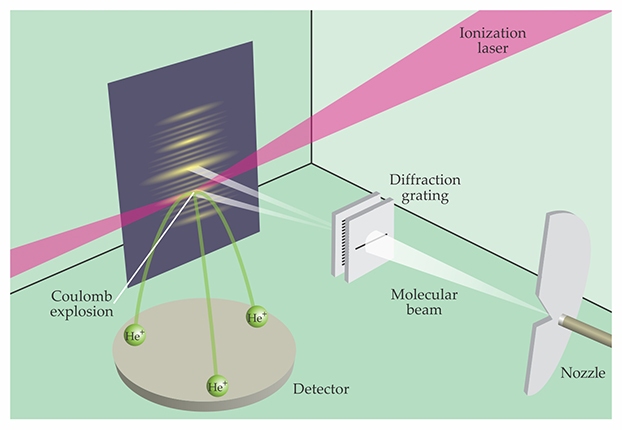
Finding the Efimov state required a three-pronged technical approach. First, Dörner and his team eliminated as much of the background as they could by lowering the pressure in the detection chamber to 10⁻¹¹ millibars—even as new He was constantly being introduced. Second, to find the conditions best suited to making Efimov trimers, they automated the apparatus to repeat the experiment over a wide range of molecular-beam temperatures and pressures. Third, they developed new data-mining and analysis techniques to identify what turned out to be 10 to 15 Efimov trimers per hour out of 6000 events per second from all other sources. Says Dörner, “This was almost like searching for a new particle in high-energy physics.”

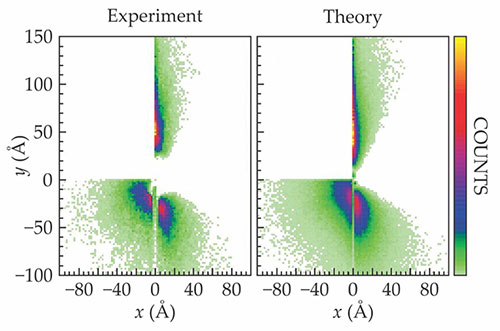
For each ionization event that was identified as an Efimov trimer, the researchers reconstructed the three atoms’ relative positions at the moment of ionization. Aggregate data are shown in figure 3. The Frankfurt experimenters were surprised by the trimer’s scalene structure. As Dörner asks, “Why should three identical particles form such a highly asymmetric system?” Dörte Blume (Washington State University), who provided theoretical support for the project, points out that the experiments agree well with the structure that theorists have known about for years. “However, a lot of researchers have been studying the Efimov effect without analyzing or appreciating the structures,” she says. “My hope is that this will now change.”

Next steps

Having gotten a first glimpse of the Efimov state, Dörner and colleagues next want to study its dynamics. Unlike ordinary molecules—but like the dimer and ground-state trimer—the Efimov trimer has no rotational or vibrational substates. Any attempt to set its constituent atoms in motion will tear it apart. Instead, the researchers plan to create coherent superpositions of the ground-state and Efimov trimers and look at how their wavefunctions change with time.

They also hope to study larger systems. Theory predicts that the Efimov effect should have an impact on clusters of four or more particles. (See the article by Chris Greene, Physics Today, March 2010, page 40 .) The He tetramer, for example, should have both a ground state and an excited, Efimov-like state. And Dörner and his group are looking for them.