Direct Measurement of the Sun’s Total Neutrino Output Confirms Flavor Metamorphosis

The 1 July issue of Physical Review Letters reports an important result from the Sudbury Neutrino Observatory (SNO), 2 km underground in an Ontario nickel mine. ¹ This much-anticipated paper describes the first direct measurement of the total flux of neutrinos (above the detector’s energy threshold) arriving from the core of the Sun, irrespective of any “flavor” metamorphoses along the way. And that total flux turns out to be in excellent agreement with the neutrino output predicted by the so-called standard solar model (SSM).

That reassuring accord does much more than simply bolster our confidence that astrophysicists understand how the Sun works. It also confirms the particle physicists’ presumption that neutrinos are capable of more tricks than the minimal standard particle theory permits: They can change flavor as they travel. That presumption has grown gradually with three decades of observed shortfalls of solar neutrinos. The nuclear processes that power the Sun can produce only electron neutrinos (v _e). And before SNO, with its innovative core of heavy water (D₂O), solar-neutrino detectors were sensitive only, or primarily, to v _e (see Physics Today, August 2001, page 13 ).

The new SNO measurement demonstrates convincingly that just about two-thirds of the highest-energy electron neutrinos emerging from the solar core have become either muon neutrinos (v _μ) or tau neutrinos (v _τ) by the time they signal their arrival by interacting with either a deuteron or an electron in the heavy water. There is good reason to believe that these are the only three neutrino varieties in nature—except perhaps for a speculative “sterile” variety that might be involved in flavor metamorphosis but would otherwise be impervious to the usual weak interactions.

Neutrino oscillation

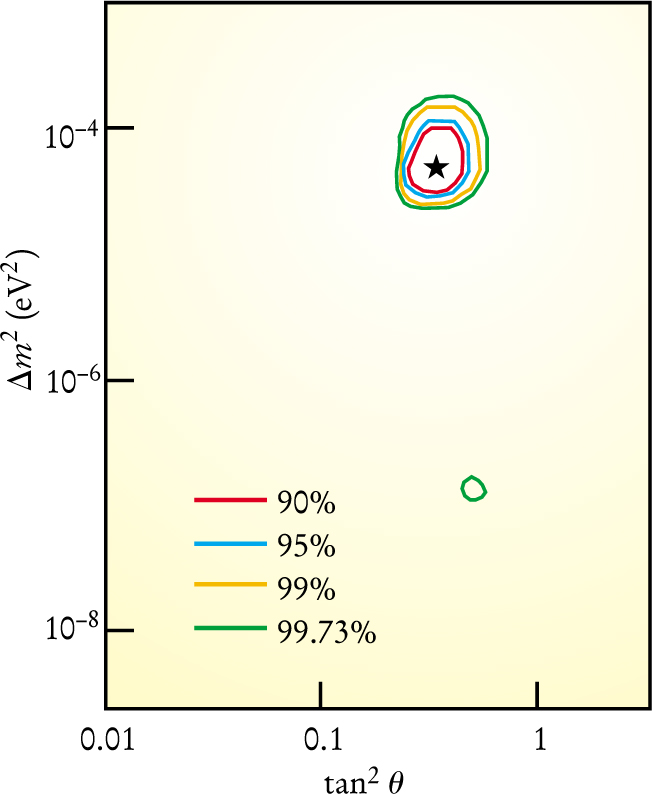
The prevailing theoretical view is that the flavor metamorphosis is a manifestation of neutrino oscillation, a phenomenon accommodated by an extension of standard particle theory. Neutrino oscillation is characterized by a transition probability that, in vacuum, oscillates periodically with L/E, the neutrino’s travel distance divided by its energy. One can make the excellent simplifying approximation that only two neutrino mass eigenstates are involved in solar-neutrino oscillation. Then, the period and amplitude of that oscillation are governed by two parameters: Δm ², the difference between the squared masses of the two mass eigenstates whose superposition makes up the electron neutrino, and θ, the mixing angle of that superposition. If all neutrino varieties were truly massless, there could be no flavor oscillation.

A companion paper reports the SNO collaboration’s finding of small differences—of at most two standard deviations—between day and night measurements of the solar-neutrino spectrum. ² At night, neutrinos must traverse Earth to reach the detector. For certain regions of the θ, Δm² parameter space, the oscillation theory predicts significant enhancement of flavor metamorphosis as a neutrino makes its way through the high electron density of Earth’s interior.

The sign and modest magnitude of the observed day-night asymmetry help to localize the parameters of solar-neutrino oscillation (see figure 1). At a confidence level of 99%, the SNO data, taken together with earlier measurements from other solar neutrino detectors, point to a Δm² of order 10⁻⁴ eV² and a rather large mixing angle θ—something like 30°. That would make v _e a roughly equal superposition of two mass eigenstates separated in mass by, at most, a few hundredths of an eV.

Distinguishing flavors

SNO, run by a collaboration of Canadian, British, and US groups led by Arthur McDonald, began taking data in 1998. The heart of the detector is a kiloton of ultrapure heavy water in a transparent acrylic vessel surrounded by 9500 photomultiplier tubes that monitor the Čerenkov light that signals neutrino interactions in the water.

The sensitivity threshold of large water-Čerenkov detectors restricts them to seeing neutrinos with energies above about 5 MeV. For neutrino interactions in a heavy-water detector that liberate neutrons, the threshold can be lowered to 2.2 MeV, the binding energy of the deuteron. But, in any case, the only significant source of neutrinos at this high-energy end of the solar-neutrino spectrum is the decay of boron-8 nuclei produced in a minor byway of the chain of fusion reactions that power the Sun. The observation of ⁸B neutrinos provides a particularly stringent test of solar models.

In its first major paper, a year ago, ³ the SNO collaboration reported on about 1000 events in which a solar v _e hitting a deuteron produced the reaction $$v_e+\text{d}\to \text{e}+\text{p}+\text{p}.$$ (1)

The instigating neutrino has to be a v _e because the reaction turns it into the telltale electron. Reaction 1 is called a charged-current (CC) interaction because it involves the virtual exchange of the charged intermediate vector boson (W^±). (The analogous CC reactions that would create the heavier μ and τ charged leptons from v_μ and v_τ require energies that are far beyond the solar-neutrino spectrum.)

Last year’s SNO result from the CC events was a v_e flux roughly a third of the⁸ B neutrino output predicted by the SSM. To see what becomes of the missing two-thirds of the predicted solar flux, the SNO detector could exploit another possible result of a v-d collision: $$v+\text{d}\to v+\text{p}+\text{n}.$$ (2)

This quasi-elastic breakup of the deuteron is called a neutral-current (NC) interaction because it is mediated by the neutral intermediate vector boson (Z⁰). Because reaction 2 can be produced with equal probability by a neutrino of any of the three flavors, it serves as a direct measure of the total flux of solar neutrinos, regardless of any flavor oscillation—assuming that none have been rendered sterile.

A year later

Detecting reaction 2 is, however, particularly tricky. So that’s why we’ve had to wait an extra year for the NC events. The neutron freed in the deuteron breakup can signal its presence through Čerenkov light generated by a 6.25-MeV γ emitted when the neutron is subsequently captured by another deuteron. But, more often than not, the neutron is captured by some other nuclear species that yields no telltale γ, or it escapes the heavy-water vessel entirely. Of even more concern is the low-level contamination of uranium and thorium in the heavy water and its surroundings. Their decay chains produce gammas that can photodisintegrate deuterons, thus creating a background of spurious neutrons.

Taking unprecedented precautions to build and maintain the detector as free as possible of radioactive contaminants, the collaboration has managed to beat down the background of nuclear decays far enough to harvest 577 NC events with an estimated background of only 44 neutrons from photodisintegrations—in 306 days of active running.

The NC yield corresponds to a flavor-blind total flux of (5.09 ± 0.62) × 10⁶/(cm² s)⁸ B neutrinos from the Sun. The SSM flux prediction ⁴ for n_e produced by⁸ B decays in the solar core is (5.05 ± 0.91) × 10⁶/(cm² s). But the SNO measurement of the flux of⁸ B electron neutrinos, now based on some 2000 CC events, is only (1.76 ± 0.11) × 10⁶/(cm² s). So here we have strong evidence that solar neutrinos change flavor en route.

The case for neutrino oscillation becomes even stronger when one includes the data for the elastic scattering of solar neutrinos off electrons: $$v+\text{e}\to v+\text{e}.$$ (3)

If the incident neutrino is a v_e , both Z and W exchange contribute to this reaction. For the other neutrino flavors, however, only the smaller Z-exchange term can contribute to scattering off electrons. Doing the calculation, one finds that the total rate for reaction 3 is proportional to the incident v _e flux plus only about 15% of the combined incident flux of v _μ and v _τ.

Thus, although reaction 2 provides the most direct and precise measure of the total incident neutrino flux, regardless of flavor, one can also measure that total flux by combining data from only reactions 1 and 3. That was, in fact, how the SNO collaboration was able to estimate the total solar-neutrino flux last year, ³ before the analysis of the reaction-2 data was ready. That result relied heavily on the accumulated e–v elastic-scattering data from the much larger Super Kamiokande light-water Čerenkov detector in Japan. ⁵

The 50-kiloton Super Kamiokande detector has to be much larger than SNO because the cross section for reaction 3, which is the only useful neutrino interaction in a light-water Čerenkov detector, is so much smaller than the deuteron interaction cross sections. Of course, a kiloton of heavy water is enormously expensive. But SNO was able to borrow the precious liquid from Canada’s heavy-water reactor program.

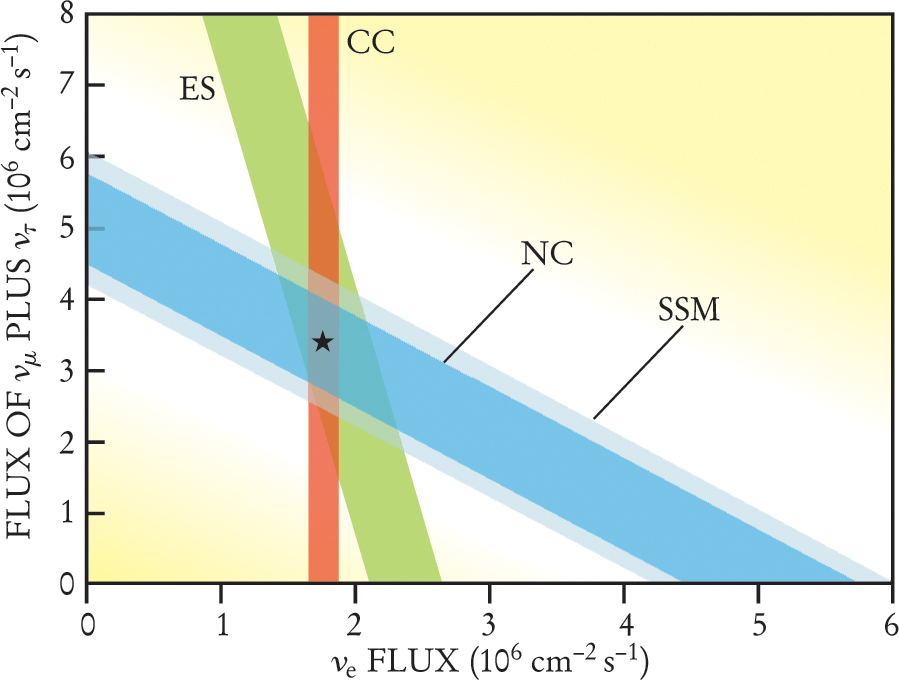
Figure 2 translates the event rates observed in SNO for the three reactions into three linear bands on a plot of the incident v _e flux against the combined flux for the other two neutrino flavors. The point where they cross yields the flavor decomposition of the arriving flux of solar neutrinos. Confidence in this decomposition is bolstered by the observation that the three experimental bands do indeed cross essentially at one point. And a fourth band, impressively shadowing the newly measured experimental band for the neutral-current reaction 2, is the SSM theoretical prediction for the total flux of⁸ B neutrinos from the Sun. The message is that the Sun’s output of electron neutrinos is just about what astrophysical theory expects, but that about two-thirds of the highest-energy solar neutrinos arrive here in altered guises.

To improve the detection efficiency for neutrons liberated in the neutral-current reaction, the SNO collaboration has recently added salt to the heavy water. Chlorine captures neutrons more readily than does deuterium, and the capture releases a more energetic g. Eventually, neutron counters filled with helium-3 will be deployed throughout the detector. Near Super Kamiokande, a new facility called KamLAND is just now getting into the solar-neutrino business. ⁶ The KamLAND detector, housing a kiloton of liquid scintillator, will not only be peering at the Sun. It also looks at surrogate “solar” neutrinos from more than a dozen power reactors 80-800 km away. Those distances and the energy spectrum of the reactor neutrinos turn out to be particularly felicitous for examining neutrino oscillation in the region of θ, Δm ² parameter space favored by the SNO solar-neutrino results.

When experimenter Raymond Davis, theorist John Bahcall, and coworkers, in back-to-back Physical Review Letters in May 1968, reported the first evidence of a shortfall of solar neutrinos, the reaction—aside from skepticism—was that the prevailing theory of the solar core must be inadequate. Now it’s quite clear that the inadequacy lay elsewhere—in our understanding of the neutrino. The complexities of neutrino physics, as they are gradually revealed in the various observational domains that appear to exhibit flavor oscillation, may turn out to be the guideposts that point the way to a more encompassing theory beyond today’s standard model of the fundamental particles.