Chaotic semiconductor lasers generate random numbers at high speed
DOI: 10.1063/1.3206082
The familiar “random number generators” used in computers and calculators are actually based on the outputs of deterministic algorithms. So although the sequences they generate may pass established statistical tests of randomness, they’re not entirely unpredictable, because an attacker could guess the algorithm itself. That’s not a problem for some applications, such as Monte Carlo simulations or randomized music playlists. But others, such as online gaming or secure communications, benefit from sequences that are truly unguessable, such as can be generated from measurements of a stochastic physical process. A simple example of such a process is the roll of a die. More sophisticated possibilities, and ones that can generate sequences more quickly and be automated more easily, involve quantum or thermal noise.
As computing and communications speeds increase, there is a growing need for faster methods of generating random sequences. Last year Atsushi Uchida, now of Saitama University in Japan, and his colleagues developed a method, 1 based on the digitized outputs of two chaotic semiconductor lasers, for producing random binary sequences at a rate of 1.7 billion bits per second—much faster than any previously developed method based on a physical process. Now, Ido Kanter, Michael Rosenbluh, and their students Igor Reidler and Yaara Aviad at Bar-Ilan University in Ramat-Gan, Israel, have found a way, using only one laser, to produce up to 12.5 billion random bits per second. 2
Laser chaos
Semiconductor diode lasers—indeed, all lasers—exhibit small intensity fluctuations that are thought to be quantum in origin. When a certain fraction of a semiconductor laser’s output is fed back into the laser, those fluctuations are amplified, and the laser’s intensity exhibits large, irregular oscillations at subnanosecond time scales, as shown in the figure. Measuring and digitizing that intensity could provide a source of random numbers, but for the fact that the laser oscillations very nearly repeat themselves with a period equal to the feedback time. If the laser light traverses a delay line a few meters long before being reinjected into the laser, as is typical, the feedback time is a few tens of nanoseconds. Choosing the period between measurements to be incommensurate with (that is, not a rational fraction of) the feedback time is not enough to solve the problem: After only a few multiples of the feedback time, the measurements come close enough to sampling the same part of the oscillation cycle that they strongly correlate with the measurements made during the first cycle.

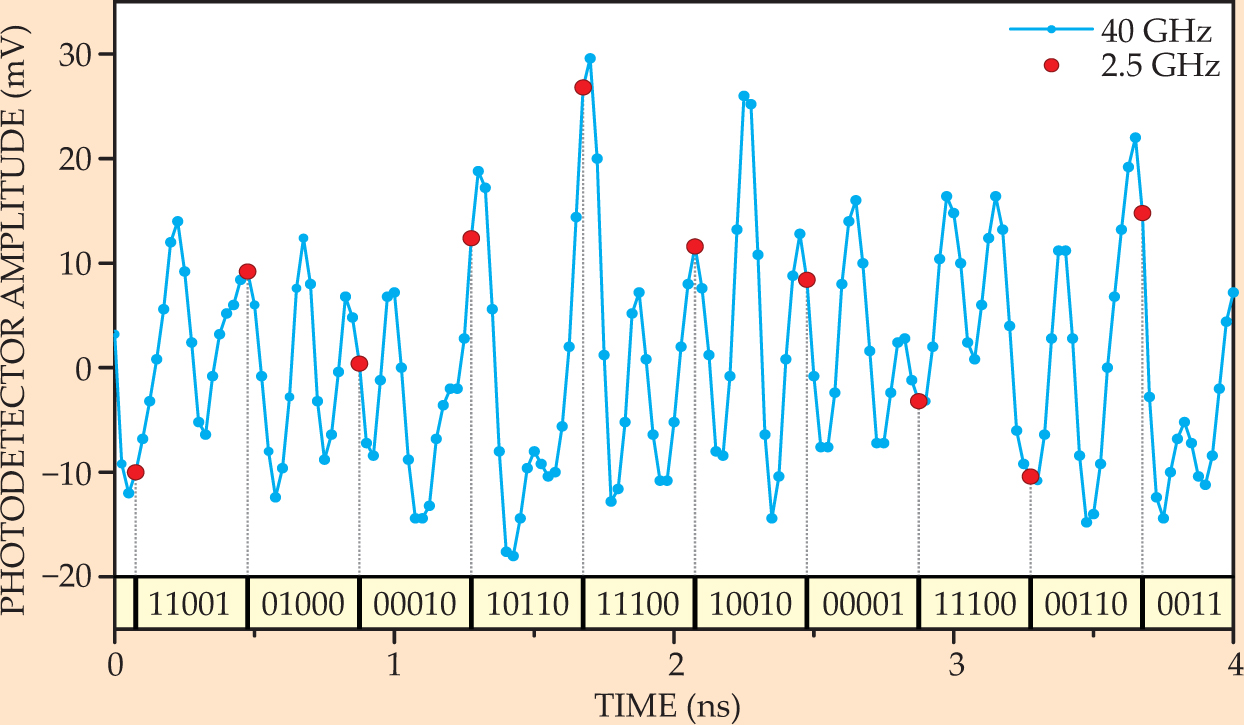
The chaotic output of a semiconductor laser sampled at 40 GHz (blue dots). Researchers from Bar-Ilan University in Israel use the output of one such laser to generate a random binary sequence by digitizing measurements taken at 2.5 GHz (red dots) into eight-bit numbers, taking the differences between consecutive measurements, and retaining from each difference the five least significant bits, shown at the bottom of the figure.
(Adapted from
Uchida and colleagues solved that problem by using two single-mode distributed-feedback semiconductor lasers with feedback times incommensurate with each other and with the sampling time. To generate one bit in their sequence, they measured the intensity of both lasers, digitized each using one-bit analog-to-digital converters (so an intensity above a threshold value becomes a “1” bit, and a lower intensity becomes a “0”), and then performed an XOR operation on those two bits.
The rate at which they could generate random bits was limited not by any aspect of their procedure but by the characteristic time scale of the chaotic laser intensity oscillations. They found that at sampling rates up to 1.7 GHz, their method generated sequences in real time that passed statistical tests for randomness. Small drifts in the lasers’ average intensities, however, could throw off the sequence’s balance of ones and zeroes, so the lasers needed to be kept carefully tuned.
Significant discard
The Bar-Ilan researchers sample the intensity of a single, inexpensive, edge-emitting diode laser—again, with a sampling time incommensurate with the laser feedback time—digitize the measurements using an eight-bit analog-to-digital converter, and compute the differences between pairs of successive measurements. For each difference, an eight-bit binary number, they discard the three most significant bits and keep only the five least significant.
Their method avoids the problem of sensitivity to intensity drifts: Even if the distribution of intensity measurements is skewed to one side or the other, the differences between measurements must be symmetrically distributed—what goes up must come down. Using only the least significant bits of each difference measurement allows them to avoid any measurable correlation between measurements made during different repetitions of the oscillation cycle. It also allows them to make measurements slightly more frequently, up to 2.5 GHz. Since each new measurement adds five bits to their sequence, they can generate up to 12.5 billion random bits per second.
References
1. A. Uchida et al., Nat. Photonics 2, 728 (2008). https://doi.org/10.1038/nphoton.2008.227
2. I. Reidler et al., Phys. Rev. Lett. 103, 024102 (2009). https://doi.org/10.1103/PhysRevLett.103.024102
More about the authors
Johanna L. Miller, jmiller@aip.org




