Beam Balance Helps Settle Down Measurement of the Gravitational Constant

The 14 October Physical Review Letters brought us a new measurement of G, Newton’s gravitational constant, by Stephan Schlamminger and coworkers at the University of Zürich. The group employed a novel method that abjures the traditional torsion balance. ¹ Why should this be of more than passing interest to anyone but a dedicated metrologist?

The 1986 compilation of fundamental constants by CODATA—the international Committee on Data for Science and Technology—gave its recommended value of G an uncertainty of 128 parts per million (ppm). That makes G, by far, the most imprecisely known constant on the list. Twelve years later, when CODATA announced its new compilation, one might have expected a decade of careful new measurements to have shrunk the uncertainty of G. But, in fact, the 1998 CODATA compilation actually raised the uncertainty of G by an order of magnitude, to 1500 ppm.

An outlier and a warning

How could there be such a retrogression? Two papers had caught the metrology community’s attention in 1995. First, Winfried Michaelis and coworkers at the Physikalisch-Technische Bundesanstalt (PTB), Germany’s national standards laboratory, measured G to be more than 40 standard deviations higher than the 1986 CODATA value. ² (See the figure at right.) Like most of the frontier measurements of G in recent decades, the PTB experiment used a modern variant of the torsion-balance design that goes back two centuries to the celebrated measurement by Henry Cavendish. Also in 1995, Kazuaki Kuroda, at the University of Tokyo, published an analysis that warned of the distorting effect of frequency-dependent nonlinearities in the torsion fibers of such instruments. ³ Cavendish’s balance was a dumbbell hanging from a torsion fiber, upon which nearby masses exerted a gravitational torque

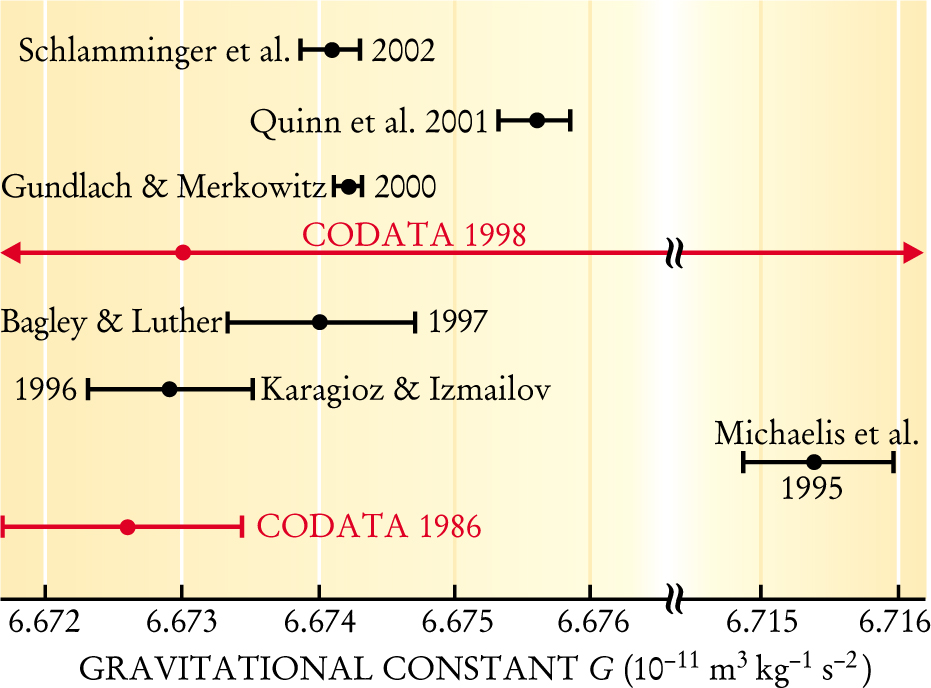
The PTB measurement incited a flurry of new measurements in a field accustomed to a more leisurely pace. And Kuroda’s warning has induced experimenters to devise new tricks that minimize what has come to be called the Kuroda effect. Since 1995, none of the new G determinations has strayed nearly as far from the consensus as the PTB measurement had. The PTB group’s torsion balance did not, in fact, hang from a fiber. And Michaelis and company have not yet found an explanation for their provocative outlier.

To date, the measurement with the smallest quoted uncertainty (14 ppm) is still the one carried out by Jens Gundlach and Stephen Merkowitz at the University of Washington two years ago ⁴ (see Physics Today, July 2000, page 21 ). They addressed the Kuroda effect by devising a novel scheme to minimize the twisting of the torsion fiber as the balance was rotated past a surrounding array of heavy steel balls. With that high-precision result, the metrologists hoped, the measurements of G would settle down for a while. But it was not to be. Last year, Terry Quinn and colleagues at the Bureau International des Poids et Mesures (BIPM) outside Paris used a modified torsion balance to measure G in two different ways designed to minimize Kuroda distortion. The result, unfortunately, differed from Gundlach’s by more than four standard deviations. ⁵

“I resolved 30 years ago that I would never try to measure G,” says Stanford University’s Francis Everitt, who devises precise tests of general relativity. “It’s been the graveyard of so many fine experimenters. That leaves one with all the more admiration for old Cavendish.”

The title of Cavendish’s historic 1798 paper, “Experiments to Determine the Density of the Earth,” reminds us that G cannot be determined simply from astronomical observation of orbiting bodies, if one does not have independent knowledge of the mass of the star or planet about which the body is orbiting. Instead, the experimenter faces the daunting task of measuring the tiny gravitational attraction between two objects of known mass in the laboratory.

A beam balance

To get away from torsion balances entirely, the Zürich group chose to measure G with a beam balance. The quoted uncertainty of this new measurement is about twice as big as Gundlach’s. But it has the important virtue of being free of systematic errors peculiar to torsion balances.

For its beam balance, the group chose and modified a commercial “mass comparator” of a kind that is regularly used by national standards laboratories to perform high-precision comparisons of secondary standard kilogram masses. (The kilogram is the last of the fundamental units that is still defined by an artifact: a platinum–iridium cylinder kept in the basement of the BIPM.) Unlike the traditional chemist’s analytical balance with its two pans and sliding counterweights, the mass comparator is a one-armed balance with a fixed 1-kg counterweight and an electromagnetic coil for fine tuning. The resolution of the Zürich group’s balance was 13 nanograms, well below the 200 ng noise level of a typical measurement.

The scheme was to measure the apparent weight difference between two identical 1.1-kg copper or tantalum test masses due to the gravitational attraction of 14 tonnes of mercury in containers that could be distributed in two different configurations. The idea came from the group’s earlier attempt to determine G by measuring the gravitational effect that the redistribution of water in a local reservoir would have on a pair of test masses. “We’ve brought the reservoir into the lab,” says Schlamminger.

The figure on page 21 shows the two test masses, vertically separated by 1.5 m, each hanging from wires that can be attached, in turn, to the beam balance. Two movable, 7-tonne cylindrical tanks of mercury that serve as the field masses can sit either together between the test masses or apart, above and below them. In each of these two field-mass deployments, the beam balance weighs the suspended test masses, one at a time. When the field masses are together, their gravitational pull on the test masses attraction makes the top test mass appear to be almost 0.4 mg heavier than the bottom one. Then, when the field masses are moved apart, the sign of this inequality is reversed.

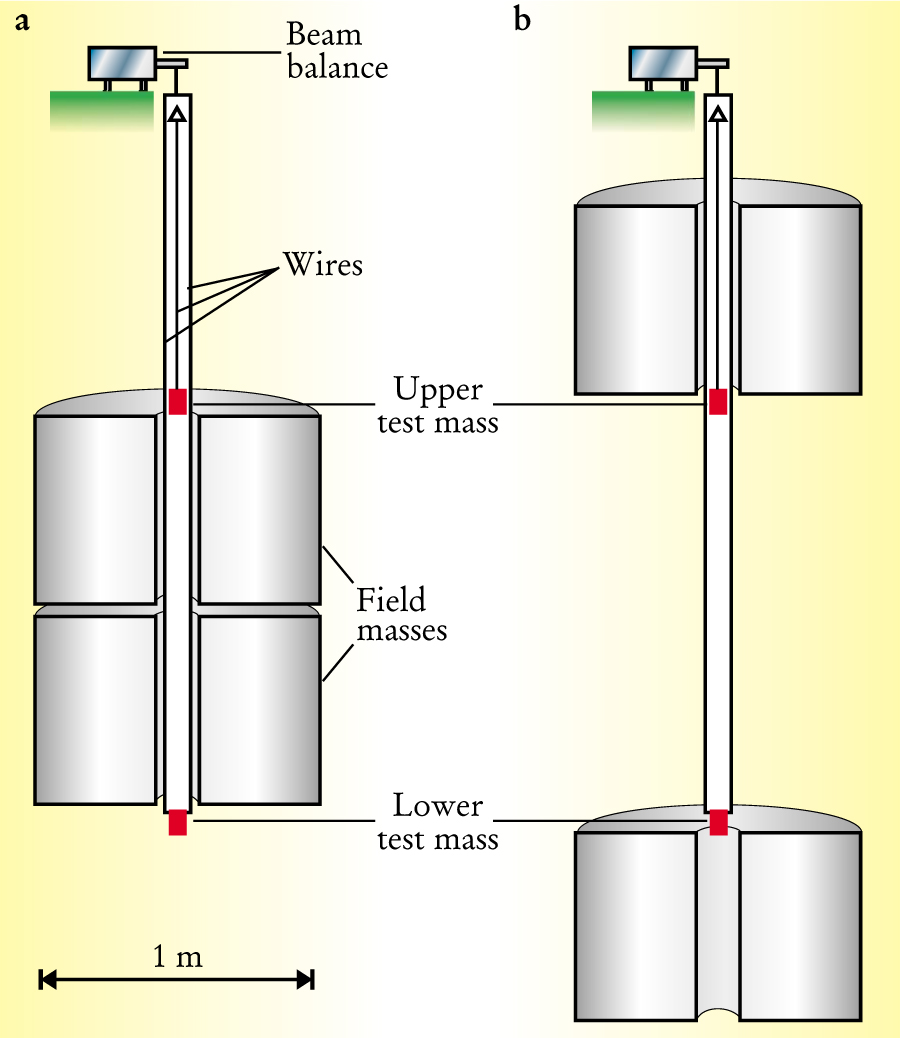
This alternating signal, modulated by repeatedly moving the field masses, is so unusually large because the mercury tanks are so massive and so close to the test masses. From measurements of the apparent weight difference in both deployments, and precise knowledge of g, the local acceleration of gravity, one can calculate G. One also needs to know the distribution of the field and test masses with high precision. Mercury was chosen not only for its very high density, but also because, being a liquid, it has a particularly homogeneous mass distribution.

The balance in the bunker

Precision measurement requires scrupulous attention to small effects. For thermal and mechanical stability, the Zürich apparatus sat in a pit 5 m deep, lined with thick concrete walls. To avoid the effects of buoyancy, air currents, and surface adsorption on the test and calibration masses, the balance and the test masses were ensconced in a vacuum system. To compensate for nonlinearities in the beam balance’s response, the weight measurements were carried out repeatedly, with a variety of small auxiliary weights added to the balance to provide different known offsets. A cycle of such measurements, with different working offsets and repeated rearrangement of the field masses, took about four days.

The Zürich group performed eight such measurement cycles with gold-plated copper test masses in the summer of 2001. The fact that the gravitational attraction to a cylindrical field mass with a narrow axial hole is maximum when the test mass is just at an entrance of the hole reduces the vulnerability of the G measurement to imprecision of the placement of the test masses. This vulnerability was even smaller in the group’s subsequent run with tantalum test masses, which are denser and therefore smaller.

Together, the measurements with the copper and tantalum test masses yielded a G of $$\left(\text{6}\text{.67407}\pm \text{0}\text{.00022}\right)\times {10}^{-11}{\text{m}}^3/\left(\text{kg}{\text{s}}^2\right)$$

The 33-ppm uncertainty is predominantly systematic rather than statistical. It is dominated by the nonlinearity of the beam balance and imperfect knowledge of the field-mass distribution.

The new result is well within one standard deviation of Gundlach’s measurement. This agreement is all the more heartening because the new experiment is so different from all the torsion balance experiments, and therefore susceptible to very different systematic errors. An important difference is that, in this latest measurement, the force exerted by the field masses is vertical. “Unlike the torsion-balance experiments,” Schlamminger explains, “we compare the field-mass attraction directly with the Earth’s attraction.”

Though it’s reassuring to see the measurements of G beginning, apparently, to settle down again, the precise numerical value of Newton’s constant is not of immediate, pressing interest for the comparison of theory with experiment. But there is a symbiosis between the new techniques developed in the quest for G and those being marshaled in the laboratory searches for non-Newtonian dependence of gravity on separation or material composition (see Physics Today, September 2000, page 22 ).

The Zürich measurement was Schlamminger’s PhD thesis experiment. His thesis supervisor, coauthor Eugen Holzschuh, died suddenly of a heart attack last November at age 53, while the experiment was in progress.