Archimedes’s principle gets updated

The fate of an object in a simple homogeneous fluid is easy to guess. If it weighs more than the fluid it displaces, it sinks; otherwise, it floats, just as Archimedes predicted 23 centuries ago. In both natural and industrial settings, though, the suspending fluid is usually complex, filled with several other dispersed species in a variety of sizes and densities.

Some of that complexity may be deliberate. Food scientists or cell biologists, for instance, often add heavy salts or colloidal nanoparticles to an already crowded fluid to create a density gradient in the solvent that will separate the different components in suspension. Proteins, nucleic acids, cell organelles, and other components sink or float to levels where their densities match that of the local solvent, in a process typically aided by centrifugation. The technique is a common way to efficiently resolve or extract the different species.

As early as the 1960s, however, researchers noticed that the apparent protein density in solution varied depending on the nature of the solvent. ¹ And recent fractionation experiments on suspensions of carbon nanotubes and graphene flakes revealed even more striking anomalies in apparent density. ² The discrepancies prompted researchers to ask what effect such fluid complexity has on the buoyant force felt by an object. Should the weight of displaced fluid in Archimedes’s principle be that of the bare solvent or the suspension? Dozens of papers advocating one or the other appear in the literature. ³

The answer turns out to be neither, according to a new study led by physicists Roberto Piazza (Polytechnic University of Milan) and Alberto Parola (University of Insubria). When the fluid is a colloidal suspension or highly structured solvent, they realized, the amount of displaced fluid can be significantly altered by density perturbations that a particle induces in its surroundings. ⁴

To see how, imagine adding a single object to a bunch of smaller ones suspended in water. In equilibrium and by themselves, the smaller particles in a given volume V experience a buoyant force that balances their own weight W = mngV, where m is the particles’ buoyant mass, n their number density, and g the gravitational acceleration. But when the test object is introduced into the same volume, the distribution of those particles is no longer uniform—it changes in a way that depends on their mutual interactions with the object.

More specifically, the interactions—which might include attractive van der Waals, repulsive coulombic, or, as illustrated in figure 1, simple hard-sphere interactions—generate a concentration profile set by a radial distribution function g₁₂(r). That function quantifies the local deviation from uniform density. Therefore, the actual weight W’ of fluid displaced in a given volume is proportional to an integral of the distribution function.

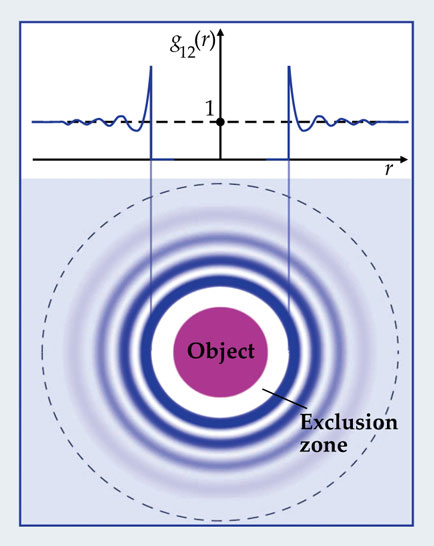
The difference between the weights before and after the object has perturbed its surroundings amounts to an excess buoyant force F beyond what Archimedes would predict: F = W’ − W = mgn∫[g₁₂(r) − 1]d³r. And in the case of hard spheres, the additional buoyancy has a simple physical explanation: It comes from the exclusion of particles from a region close to the submerged object, within which the surrounding particles cannot go. In short, the excluded volume has to be included as part of the total displaced fluid.

Generally, the effect is to lower the effective density of an object in suspension. But not always, because the excess buoyant force may not oppose gravity. A particularly strong attractive contribution to the mutual interaction could shrink the exclusion zone of an object enough—as neighbors glom onto it, say—that the object may be pulled down and thus appear denser than it really is. Alternatively, one might have a suspension of bubbles that, if somehow repelled by an object sitting among them, also leads to the objects’ sinking.

Size matters

The larger the submerged object relative to its neighbors, the smaller the excess buoyancy. So to test their theory, Piazza, Parola, and their colleagues studied the behavior of differently sized thermoplastic polymethyl methacrylate (PMMA) particles in aqueous suspension. Specifically, to three separate suspensions of MFA spheres (a polytetrafluoroethylene copolymer), each with a radius of 90 nm, they added minute amounts of PMMA of radius 220 nm, 300 nm, or 400 nm.

The MFA colloids, although spherical and dispersed, are partially crystalline and therefore birefringent. Thanks to that optical anisotropy, depolarized light scattering is an accurate probe of their local concentration, which gradually increases with depth as the particles pack closer together. By vertically scanning a softly focused laser beam along the suspension, the researchers measured the concentration profile and thus the suspension’s density as a function of depth.

After waiting a month for the mixture to equilibrate, they spotted the PMMA particles as a thin whitish layer lying in the clear suspension. From Archimedes’s principle, one would expect the differently sized PMMA spheres to settle to a single level at which the material’s density matches that of the local fluid around it. But they actually settled to progressively higher spots in the column—the smaller the PMMA, the higher it floated, in agreement with the researchers’ generalized principle.

In the opposite case of small, dense particles settling in a sea of larger but lighter ones, the theory predicts far stranger consequences. When Parola was working out the theory last year, he was struck by the fact that the density perturbations induced by a large particle could generate an excess buoyant force that amounts to a sizable fraction of the smaller particle’s weight—strong enough to push it to the surface despite its greater density. Indeed, one of the team’s experiments, outlined in figure 2, bears that out: Gold particles only tens of nanometers in diameter but nearly 20 times as dense as water were found—again after a month’s equilibration—to float on an MFA suspension whose density is only slightly greater than water’s.

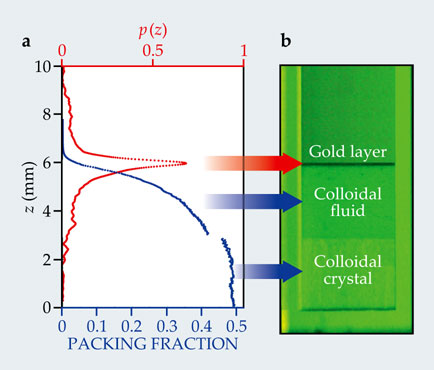
Evidently, as the tiny gold particles diffuse through the suspension, they carry with them enough bare solvent—far more than the volume displaced by gold alone—to offset the huge density disparity between the two materials. The striking effect occurs despite the colloids’ size—just five times as large as the gold particles. Even Archimedes would have been surprised.