Analysis quantifies effects of tides in Jupiter and lo

Moons and planets aren’t point particles, and their finite sizes and lack of rigidity affect their orbits. For example, the Moon’s gravity raises a tidal bulge in Earth’s oceans. Because Earth rotates faster than the Moon orbits, that bulge is always pushed slightly ahead of the line between Earth and the Moon, and the gravitational attraction between the Moon and the bulge pulls Earth backward in its rotation and the Moon forward in its orbit: Our days are getting longer, and the Moon is gaining energy and thus receding.

The same phenomenon occurs between Jupiter and its moons, particularly its innermost large moon, Io. On the other hand, Jupiter also raises a tidal bulge in Io, which causes lo to lose energy. Now the Paris Observatory’s Valéry Lainey and colleagues have teased out the previously unknown magnitudes of the Jovian system’s tidal interactions by analyzing 116 years’ worth of observations of the moons’ orbits. ¹

Many moons

Several dozen of the bodies orbiting Jupiter are classified as moons, but the largest by far are the four discovered by Galileo in 1610. In order from nearest to farthest from Jupiter, they are Io, Europa, Ganymede, and Callisto. Europa, the smallest of the four, is more than 7000 times as massive as Jupiter’s fifth and next largest moon, Himalia. Io, Europa, and Ganymede are in a Laplace resonance, meaning that their orbital periods form small-integer ratios: Approximately every seven Earth days, Jupiter is orbited by Ganymede once, Europa twice, and Io four times. The resonance has an effect on their orbits and how they influence one another.

In isolation from other satellites, moons tend to settle into synchronous rotation (meaning that the orbital period is equal to the rotational period) and circular orbits. The Galilean moons are in synchronous rotation, but because of the Laplace resonance, their orbits are not circular. For example, Io’s and Europa’s point of closest approach, where Europa pulls Io outward, is always at the same place in their respective orbits. That repeated tug gives Io’s orbit a nonzero eccentricity. Furthermore, the Laplace resonance means that any change in Io’s orbit strongly affects both Europa and Ganymede, and vice versa.

Battle of the bulges

Io is the only one of the Galilean moons to have significant tidal interaction with Jupiter. The moon creates a tidal bulge in the planet (as shown in panel a of the figure), which increases Io’s orbital energy at the expense of Jupiter’s rotational energy. By the virial theorem, when an orbiting body’s energy increases, its kinetic energy decreases while its potential energy increases by twice as much. So although Jupiter’s tidal bulge pulls Io forward in its orbit, its net effect is to slow Io’s motion.

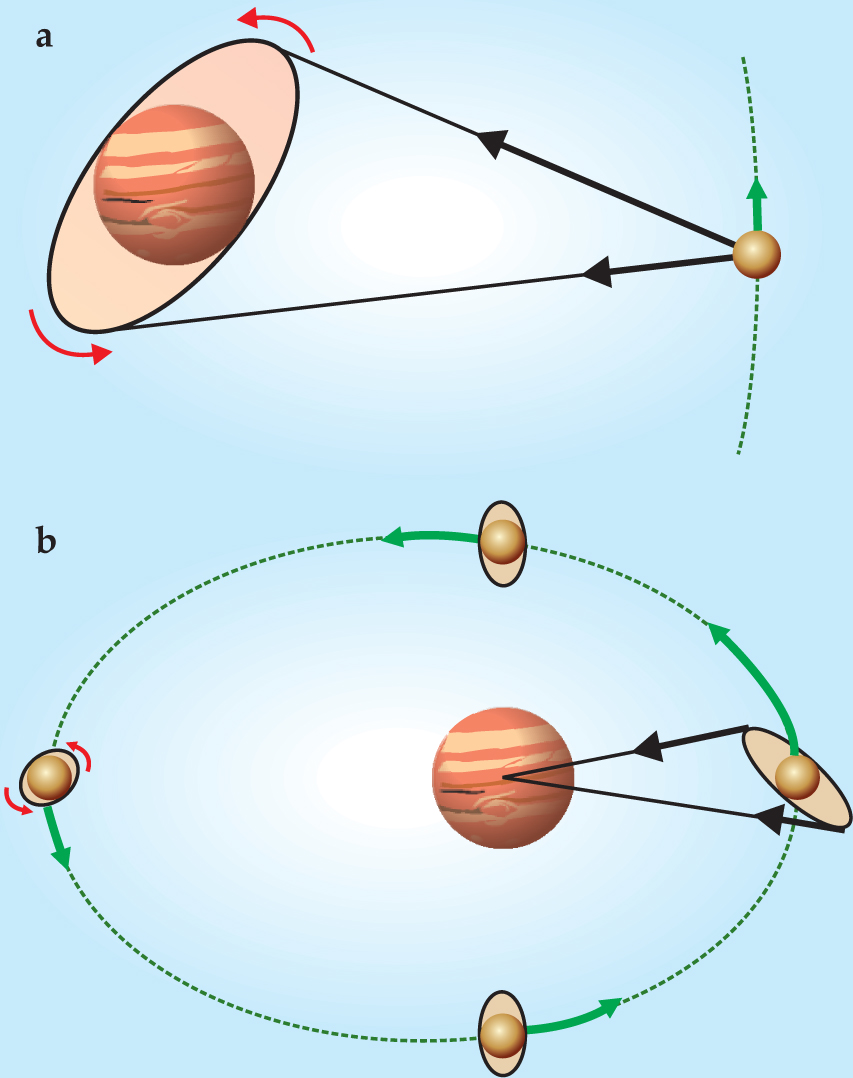
If Io’s orbit were circular, the tidal bulge that Jupiter generates in the rocky moon would have little effect, because it would always be aligned with the Io–Jupiter line. But the slight ellipticity of Io’s orbit has two consequences, as shown in panel b. First, as the Io–Jupiter distance changes, so too does the gravitational force felt by Io, and therefore the size of the bulge. Second, because Io is not always moving at the same angular speed, its instantaneous orbital and rotational rates are not perfectly matched. At its farthest point from Jupiter—the apojove—Io is spinning faster than it is orbiting, so the tidal bulge lies slightly ahead of the Io–Jupiter line in the direction of Io’s rotation. Thus Jupiter exerts a torque on Io that slows the moon’s rotation and adds to its orbital energy. At the other side of the orbit—the perijove—the opposite occurs: Io is orbiting faster than it is spinning, the bulge lags behind the Io–Jupiter line, and the planet’s gravity increases the moon’s rotational energy at the expense of its orbital energy. And since the bulge is larger and the gravitational attraction is stronger at the perijove, its influence wins out: Io’s tidal bulge causes Io to spiral inward toward Jupiter. Much of the energy that goes into growing, shrinking, and shifting the bulge is dissipated through friction; the resulting heat is thought to be responsible for Io’s volcanic activity, the most dramatic in the solar system.

Which tidal effect is stronger, and whether Io’s total energy is actually increasing or decreasing, depends on how severely Io and Jupiter are distorted by tidal forces. Those things can’t easily be observed from Earth. To infer the tide-induced accelerations from observations of the moons’ orbits, one must track the Jovian moons for a long time. The earliest usable measurements of the moons’ positions are photographic plates that date back to 1891. But the positions must be determined with much greater precision than any individual hundred-year-old measurement—or even many modern measurements—can provide. Averaging many measurements helps, but the positions must also be constrained through use of a model.

Tides over time

Several groups in the past have attempted to derive the orbital accelerations of Jupiter’s Galilean moons from the records of their positions. ² But they’ve always done it by treating the tidal effects as secular accelerations—that is, by modeling the system in the absence of the tidal effects and deriving the tide-induced accelerations from the differences between the actual trajectories and the modeled ones. The dynamical models they used have systematic uncertainties similar in magnitude to the accelerations themselves. And the method of secular accelerations doesn’t allow any conclusions to be drawn about the tidal magnitudes: Since tides in Jupiter and tides in Io have similar but opposite consequences for the moons’ orbits, the two effects can’t be decorrelated by looking at the orbital accelerations alone.

Lainey and colleagues were the first to include the tidal effects directly in a model. They numerically integrated the orbits, in two-hour time steps, from 1891 to 2007. Then they iterated the integration to fit the 26 parameters of their model: the initial position and velocity vectors of each of the four moons (they included Callisto even though it’s not in the Laplace resonance and doesn’t interact strongly with the others) and Jupiter’s and Io’s susceptibility to tides. They were able to separate the two tidal mechanisms because Io’s tides had a substantial effect on the eccentricity of Io’s orbit, whereas Jupiter’s tides had a much smaller effect.

The calculation revealed that Io is speeding up and thus spiraling inward and losing energy, whereas Europa and Ganymede are slowing down, spiraling outward, and gaining energy: At the end of the 116-year period, Io is 55 km farther ahead in its orbit than it would have been without any acceleration, Europa is 125 km behind, and Ganymede is 365 km behind. From Io’s tidal parameter, Lainey’s collaborators özgür Karatekin and Tim Van Hoolst, geophysicists at the Royal Observatory of Belgium, determined how much heat is generated by Io’s shifting tidal bulge. They concluded that if heat were lost from Io at the same rate as it was generated, the average heat flux at Io’s surface would be 2.24 ± 0.45 W/m². Io’s actual heat flux has been measured several times from IR spectral data, ³ with most estimates being between 2 and 2.5 W/m². It appears, therefore, that Io is close to a thermal steady state—that its volcanic activity is driven by the heat generated by tidal friction now, rather than by heat retained from a past period when tides might have been even higher.

Longer-term trends?

Lainey and colleagues reconstructed what happened to Io, Europa, and Ganymede over a period of 116 years. But on the time scale of orbital evolution, 116 years is just the blink of an eye. What’s next for the Jovian moons? It’s hard to tell, because the evolution the researchers found is not sustainable. Since Io’s orbital period is shortening while Europa’s and Ganymede’s are lengthening, the moons are evolving out of their Laplace resonance. Once the resonance is broken, Io’s orbit will lose its eccentricity, so the tidal bulge in Io will no longer grow and shrink and will no longer be susceptible to torque from Jupiter. That means no more spiraling inward and, most likely, no more volcanism. The present results don’t offer any predictions, though, about how soon the resonance will be effectively broken, how much Io’s orbital energy will ultimately decrease, or what will happen once it starts increasing again.

“Moving out of resonance and Io’s inward spiraling are both expressions of an evolution that cannot persist,” says David Stevenson of Caltech. “That’s the story of greatest interest, I think. It’s also the part we understand least well.”