A photonic crystal sets a peculiar trap

In 1929 John von Neumann and Eugene Wigner proposed a most unusual electron trap—one that could confine an electron whose energy exceeds that of its surrounding potential barrier. ¹ The trick was to shape the trapping potential so that the electron’s available paths of escape interfere destructively. The result is what’s known as a bound state in the continuum (BIC), a localized state whose energy lies within the continuous band normally reserved for spatially extended states.

An electronic BIC has never been achieved in an experiment, but recently researchers have sought to find its optical analogue—a bound state of light in the radiation continuum. Two years ago a group at the Technion–Israel Institute of Technology successfully generated an optical BIC in a system of waveguides, but they used a strategy quite different from the one von Neumann and Wigner envisioned. ² In the Technion group’s trap, symmetry incompatibility, not destructive interference, thwarts light’s escape: The bound state was an antisymmetric mode, which meant it couldn’t couple with surrounding waveguides designed specifically to support a continuum of symmetric modes.

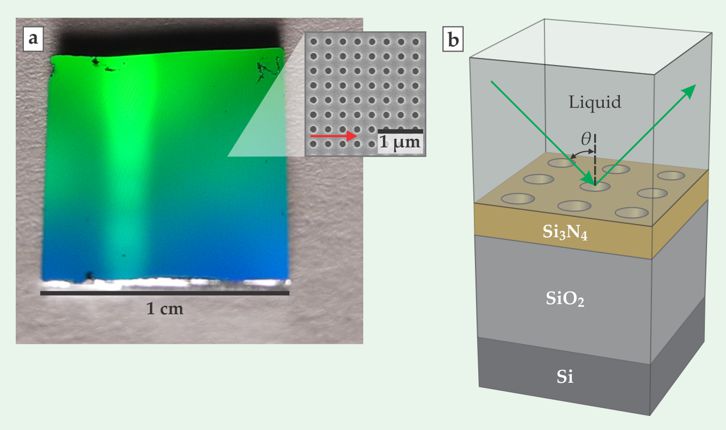
Now an MIT group led by John Joannopoulos and Marin Soljačić has demonstrated an optical BIC that arises even when symmetry makes no such demands. ³ The MIT researchers observed their BIC in a photonic crystal, a periodically nanostructured material designed to control the propagation of light. The 180-nm-thick crystal, shown in panel a of the figure, is patterned with nanoscale holes that give rise to a discrete set of internal optical modes. Some of those modes, usually the lower-energy ones, undergo total internal reflection at the crystal’s surface and remain permanently trapped; others, typically the higher-energy ones, are resonances that couple to free space and allow light to escape.

Each resonance can be described as a superposition of plane waves. If those plane waves happen to interfere destructively everywhere outside the crystal, then photons can’t escape—just as was the case for von Neumann and Wigner’s hypothetical electron. Finding one of those special resonances, however, is a bit like finding a needle in a four-dimensional haystack: Four independent quantities—the real and imaginary parts of two independent light polarizations—must cancel simultaneously.

Symmetries help to simplify the task. The time reversibility of Maxwell’s equations and the inversion symmetry of the crystal combine to eliminate one degree of freedom; mirror symmetry eliminates another. Unlike in the Technion experiment, the symmetric constraints don’t affect light’s ability to couple with free space; they simply restrict the modes that can exist within the crystal. Narrowing the possibilities still further, simulations by graduate student Chia Wei Hsu predicted a single bound state along each of four symmetrically equivalent directions, one of which is indicated by the red arrow in the inset of panel a.

From there, the search was relatively straightforward. As shown schematically in panel b of the figure, Hsu and colleague Bo Zhen angled a beam of light at the crystal to excite its various resonant modes. (To preserve the mirror and inversion symmetries, they immersed the crystal in a liquid whose index of refraction matched that of the crystal’s silica substrate.) From the widths of peaks in the reflectivity spectra, the researchers could calculate resonance lifetimes for a range of incidence angles θ. They found that as θ approached 35°, those lifetimes tended toward infinity—exactly as one would expect for a BIC.

In the parameter space near the BIC, the photonic crystal acts as a high-quality, tunable optical cavity. The group measured quality factors as high as 10⁶, and even larger values are possible in theory. (The quality factor corresponds roughly to the average number of round trips a photon makes inside a cavity before escaping.) The researchers anticipate that such an optical device could deliver practical payoffs: Concentrating large electromagnetic fields near a surface and looking for resonance shifts due to the presence of adsorbed molecules is one promising strategy for chemical and biomolecule sensing.