A photonic crystal localizes light in two dimensions

In 1958 Philip Anderson predicted that when a crystal is disordered enough—filled with a high concentration of defects, say—electron diffusion will cease. ¹ The phenomenon, called Anderson localization, explains the phase transition in a material that changes from a conductor to an insulator as disorder is increased and its electrons transform from diffusive, delocalized waves into localized, or trapped, wavepackets.

Researchers have been using Anderson’s model for decades to account for materials’ electronic properties, but they still struggle to calculate details of the phase transition; the strong interactions among electrons and between electrons and phonons complicate the problem because they can alter the local potential and the phase coherence of electrons. To estimate the critical exponents in equations that describe the transition, theorists must resort to a scaling theory based on postulates about the nature of a solution.

At the time, Anderson thought of electron localization in the context of quantum tunneling between lattice sites. In 1984 Sajeev John realized that it could be reinterpreted purely as an interference effect from multiple scattering. ² Accordingly, electromagnetic, acoustic, seismic, or any other classical wave could, in principle, be trapped within a medium that scatters strongly enough. John has since pioneered the field of light localization.

Unlike electrons, photons do not interact with each other, a simplification that makes optical experiments an ideal platform for studying Anderson localization. Photons do, however, interact with matter, and the challenge in optical experiments is to distinguish localization effects from absorption.

In a nearly perfect, or homogeneous, dielectric, light travels ballistically, scattering only occasionally from defects. An increase in disorder produces a concomitant increase in the scattering probability as light diffuses through the medium. In this diffusive regime, the same Ohm’s law holds for light as for electrons: The transmission intensity decreases linearly as sample thickness increases. In three-dimensional materials, once the disorder is high enough that the mean free path becomes comparable to light’s wavelength, the light becomes spatially trapped—effectively a standing wave held within countless random cavities—and its intensity decays exponentially with thickness. Over the past decade, a few groups have observed localization by monitoring deviations from classical diffusive behavior, typically using dielectric powders that strongly scatter the light.

Tal Schwartz, Guy Bartal, Shmuel Fishman, and Mordechai Segev—all researchers from the Technion–Israel Institute of Technology in Haifa—have now performed a different kind of localization experiment, one designed not to bring light to a standstill but to confine it in two dimensions. ³ Segev, the team leader, reasoned that if a system could be prepared in which the refractive index was disordered in two dimensions but invariant in the third, then the system could confine an incoming light beam as it flowed downstream, much as an optical fiber confines a propagating wave.

While at a conference this past summer, Schwartz learned that researchers led by Ad Lagendijk from the FOM Institute for Atomic and Molecular Physics in Amsterdam had actually predicted the effect and proposed, but never implemented, the same approach some 17 years earlier. ⁴ The advantage of the concept, known as traverse localization, lies in its geometry: The spatial evolution of the light in the propagating direction z can be mapped, Lagendijk realized, onto a Schrödinger equation that describes the evolution of a wavepacket, but with z replacing time. Researchers can thus measure localization in space rather than deduce it from a transmission spectrum.

Photonic engineering

As a first step toward measuring localization, Segev and company prepared a 2D photonic crystal—a periodic lattice that diffracts light in much the same way that a semiconductor diffracts electrons. The optical properties of a nonlinear crystal change with light intensity. By shining three intersecting laser beams within such a crystal, they could exploit interference to imprint a 2D periodic pattern onto its refractive index. Then, to introduce disorder, the group added “speckled” light to the lattice by shining yet another laser beam through a diffuser, which randomized the light’s phase and amplitude.

As a 2D effect, for which scaling theory predicts no sharp transition between diffusive and localized behavior, transverse localization arises from an exceedingly small amount of disorder—small fluctuations in the 10⁻⁴ index contrast that defines the photonic lattice. The sensitivity allowed the group to reach the level of disorder required to see the effect by simply increasing the relative intensity of the diffused laser beam.

Crucial to observing transverse localization, however, is ensuring that the index of refraction vary only in the x–y plane, with each index value remaining fixed along z. That is the equivalent of having the potential frozen in time in the Anderson model. To keep the interfering plane waves invariant in that direction, Schwartz had only to arrange the waves symmetrically around the z axis. Eliminating the diffraction of the speckled beam was less intuitive, but passing the light through a conical lens placed some distance before the diffuser did the trick. The optics produced a grainy pattern in the lattice in the form of a random superposition of plane waves, all with a common wave-vector projection in z.

With the disordered lattice set up, the researchers launched a weak probe beam and imaged the intensity distribution in the x–y plane downstream as the light passed through the material (see the figure). In transverse localization, a narrow beam propagating through a disordered medium undergoes diffusive broadening until its width becomes comparable to the localization length. The greater the disorder, the faster the beam evolves into the localized state.

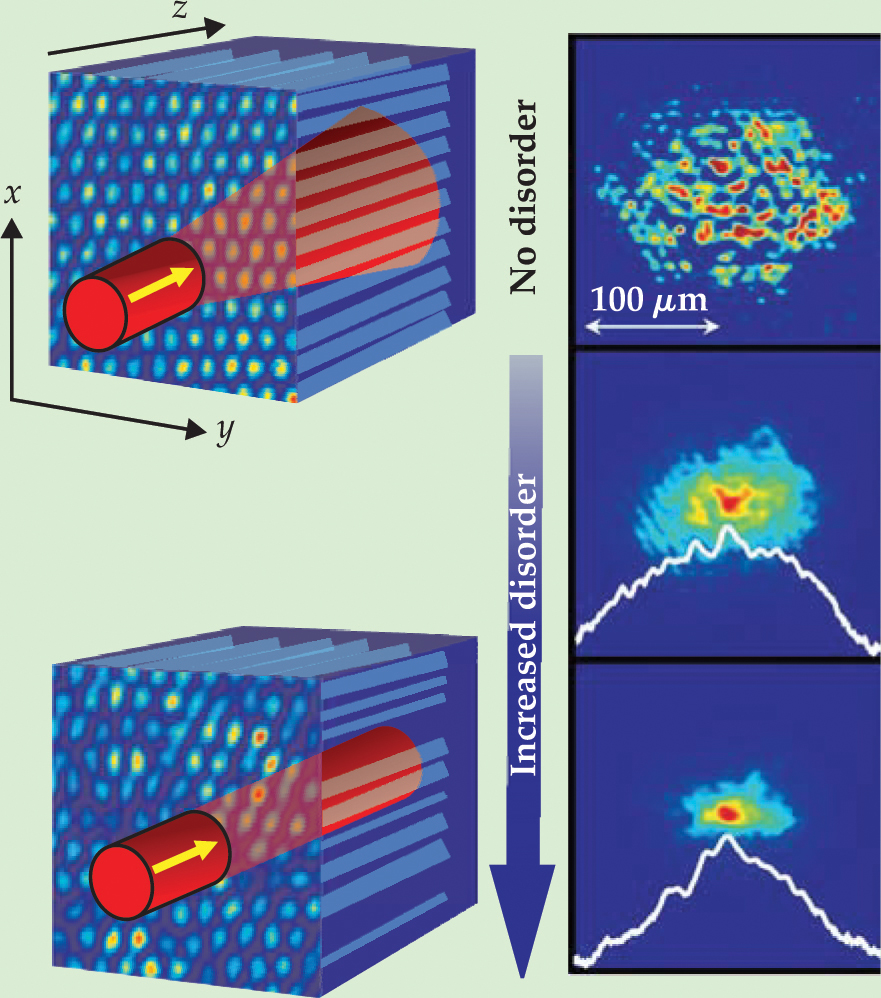
To describe the transport properties of the disordered lattice, Segev’s team measured the light-intensity distribution through various scattering regimes. When the 10⁻⁴ contrast in refractive index fluctuates by 15%, light scatters randomly among lattice sites. Adding progressively greater disorder, the researchers monitored the evolution of the output image, which eventually revealed the signature effect of Anderson localization—an exponential falloff in the light intensity through the beam’s cross section.

Central to the concept of localization are large statistical deviations in repeated intensity measurements of the same experiment. Because the intensity can vary wildly—owing to the effects of multiple interference—the researchers averaged 100 different measurements of the effective beam width for each level of disorder. To do that, they rotated the diffusion filter before repeating each measurement; each rotation altered the particular disorder pattern imprinted on the lattice.

Nonlinearity

In Segev’s experiment, increasing the laser power offers a path to explore the interplay between disorder and the nonlinear response of photorefractive crystals ⁵ (see the article by David Campbell, Sergej Flach, and Yuri Kivshar in Physics Today, January 2004, page 43 ). As the probe beam’s power rises, so does its influence on the local refractive-index modulation. The beam’s intensity has a Gaussian profile that causes the profile’s width to slightly narrow while traveling through the lattice. This self-focusing tends to enhance the transverse localization.

Although the addition of nonlinearity to the mix complicates the system, it offers a new tool for studying the emergence of exotica such as solitons, discrete breathers, and other wave instabilities. And as a source of new physics, it whets the appetite for a deeper understanding of the transition between localized and delocalized states in materials.