A nonbiological system offers insight into biological synchronization
DOI: 10.1063/1.3120884
Many biological systems —from cells to tissues to whole organisms—exhibit rhythmic or oscillatory behavior. And those oscillations can synchronize: Fireflies can flash in unison, and neurons and heart cells operate in synchrony. To gain an understanding of how such synchronizations arise, biologists often look at populations of single-celled organisms that display collective oscillations in cellular processes like metabolism. But the complexity of living cells makes unraveling the synchronization mechanisms a challenge.
Now, researchers led by Kenneth Showalter of West Virginia University (WVU) have studied a nonbiological system of thousands of oscillators and found that the system undergoes two types of synchronization transition thought to occur in biological systems. 1 Their system is simple enough to be theoretically understood and mathematically modeled. Showalter and colleagues’ work is relevant to populations of globally coupled oscillators—that is, systems in which each oscillator is linked to all the others, whether through a common electric potential, exchange of a signaling chemical with an external bath, or other means.
The two types of transition the researchers observed are a Kuramoto-type transition and a dynamical quorum-sensing transition. In the Kuramoto transition—named after Yoshiki Kuramoto, who developed much of its mathematical formalism—individual components of the system oscillate out of synchrony at low number density and gradually synchronize at higher number density. In the dynamical quorum-sensing transition, components do not oscillate at all at low number density, and above a threshold density they suddenly begin oscillating in near-perfect synchrony.
Chemical oscillations
The researchers used a form of the oscillating Belousov–Zhabotinsky (BZ) reaction based on the catalyst ferroin, which doubles as an indicator as it oscillates between its red, reduced form and its blue, oxidized form. The major features of the reaction are shown in figure 1. In one process in the oscillation cycle, shown in figure

Figure 1. The major features of the Belousov–Zhabotinsky reaction, with the dominant reactions and chemical species shown in boldface for two processes in the reaction’s oscillation cycle. (a) The activator species HBrO2 catalyzes its own production from HBrO3: Each HBrO2 molecule produces two BrO2 radicals, which go on to produce two more HBrO2 molecules. In the process, the catalyst ferroin is converted from its red, reduced form to its blue, oxidized form. (b) When enough of the ferroin is oxidized, it reacts with bromomalonic acid (BrMA) to produce reduced ferroin and the inhibitor species Br−, which draws HBrO2 out of the system and thereby shuts off the autocatalysis. When the level of oxidized ferroin falls and Br− production diminishes, HBrO2 autocatalysis can begin again. In the experiments performed by Kenneth Showalter and colleagues,
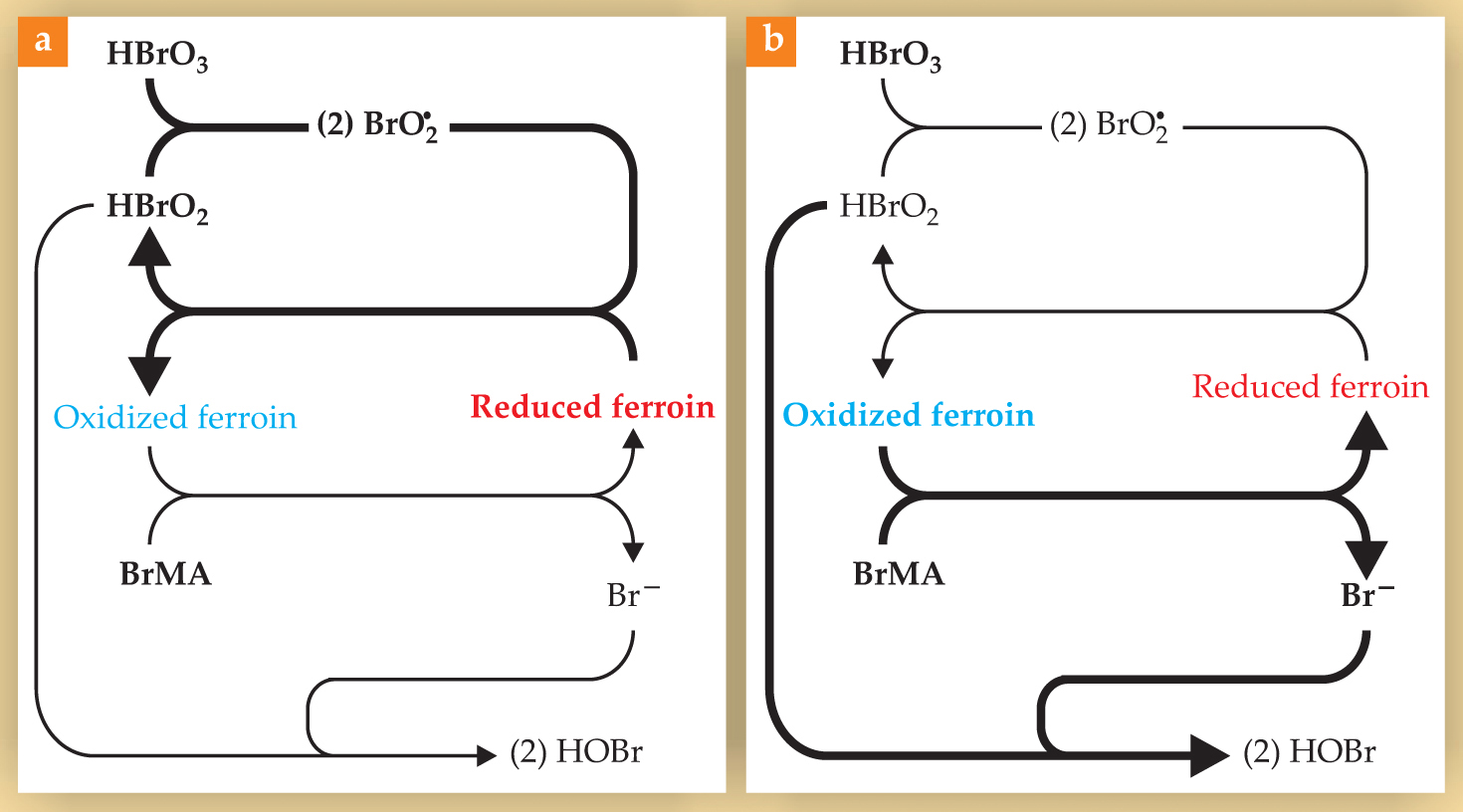
The newly oxidized ferroin then reacts with bromomalonic acid (BrMA, another abundant reagent), as shown in figure
In the system the researchers studied, the ferroin was loaded onto porous cation-exchange particles 200 µm in diameter, which were placed in a solution containing the rest of the chemical species. On each particle, the reaction proceeded as described above; in the rest of the solution, HBrO2 could not be produced (since that would require ferroin), but it could be consumed by reacting with Br−.
The idea of looking at a BZ reaction with the catalyst immobilized on cation-exchange particles originated in Showalter’s 1989 work with Jerzy Maselko. 2 The system was first used as a model of biological synchronization in a 2006 study by Annette Taylor of the University of Leeds, her student Rita Toth, and Mark Tinsley of WVU. 3 They found that when they stirred the reaction mixture, particles underwent a Kuramoto-type synchronization transition.
In an unstirred mixture—or in a stirred mixture with few particles—each particle oscillated with a different period on the order of 30–60 s. But at higher particle densities, stirring caused an exchange of chemicals between each particle and the rest of the solution, allowing the oscillations on each particle to influence the others. As a result, the particles’ oscillations aligned in both frequency and phase.
Kinetics
As chemical reactions go, the BZ system is complex—many more steps and species are involved than are shown in figure 1. But it is still simple enough that Toth, Taylor, and Tinsley were able to reproduce their experimental results using a kinetic model of the BZ reaction 4 —a system of coupled differential equations to describe the time-dependent behavior of each reaction step—that they modified to account for the exchange of chemicals between the particles and the solution. They parameterized the exchange using a rate constant k ex; to fit their data, they set k ex to a fairly low value. But they found that at higher values of k ex, corresponding to faster stirring rates, their model predicted very different behavior from the Kuramoto-type transition they observed in their experiments. At high k ex and low particle density, simulations showed that HBrO2 was removed from the particles so quickly that it couldn’t catalyze the production of more of itself, so the rate of ferroin oxidation never rose high enough to change the particles from red to blue. But in simulations at higher number density, so many particles were producing HBrO2 that it accumulated in the solution faster than it could be removed by Br−, which in turn slowed its loss from the particles and allowed it to accumulate on them. The simulated particles began to oscillate, suddenly and in near-complete synchrony. In short, the model predicted a dynamical quorum-sensing transition.
Showalter began a collaboration with Taylor and Tinsley to look for the quorum-sensing transition experimentally. Taylor went to visit WVU, where she and Tinsley continued their computational work and taught Showalter’s students Fang Wang and Zhaoyang Huang some of the experimental methods. Together, the researchers captured images of the particles on high-speed video, as shown in figure 2, and monitored bulk oscillations by measuring the electrical potential of the solution. Says Showalter, “We were surprised and delighted to see both transitions in essentially the same system in both the experiments and the computational model.”
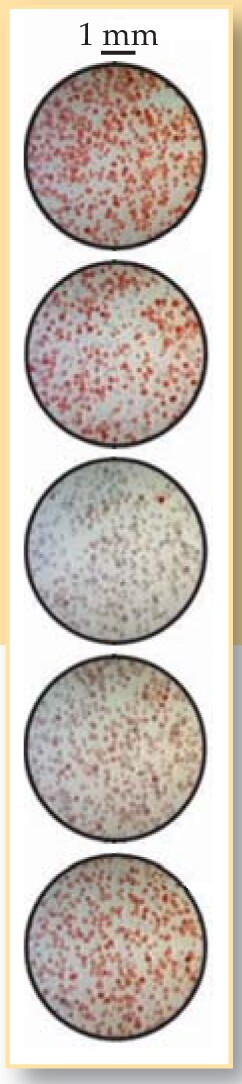
Figure 2. Frames from a high-speed video taken over the course of a nearly synchronized oscillation.
(Adapted from
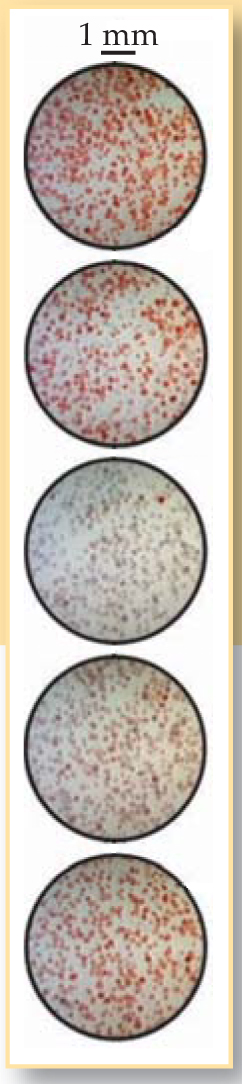
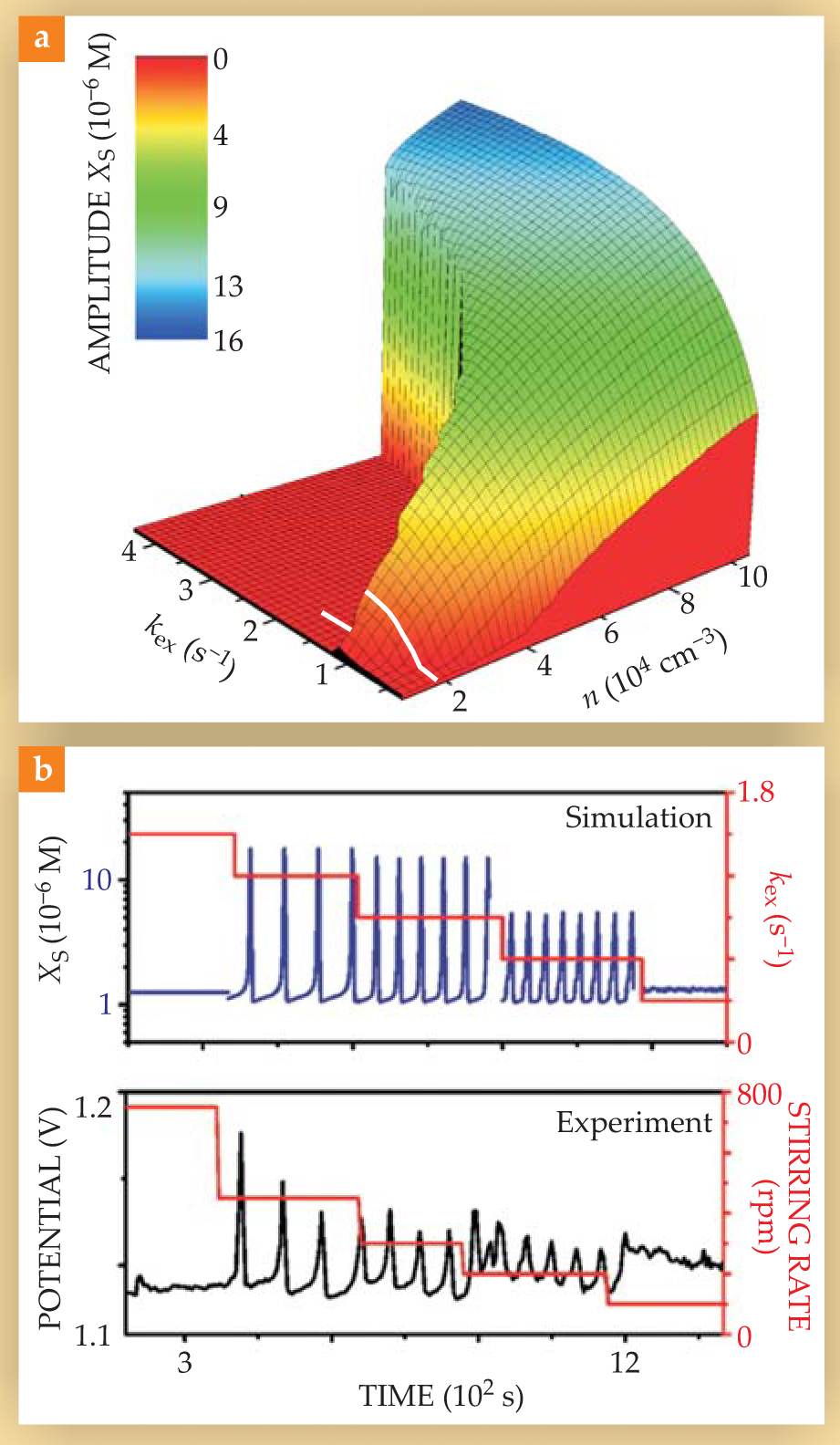
Figure 3(a) shows the results of the model. The horizontal axes represent the exchange constant k ex and the particle number density; the vertical axis and color scale show the amplitude of oscillations of the concentration of HBrO2 in the solution, a measure of the coherence of the particles’ oscillations. When the particles are unsynchronized or not oscillating at all, the amplitude is zero or nearly zero; when they are partially synchronized, the amplitude is low; and when they are fully synchronized, the amplitude is high. At low values of k ex, the amplitude increases smoothly with increasing density, and at larger k ex, the amplitude is zero at low density and jumps sharply at higher density.

Figure 3. Oscillations in X s, the concentration of HBrO2 in the solution, as a function of the exchange constant k ex and the particle number density n. At low values of k ex, the amplitude increases smoothly with increasing n as the particles undergo a Kuramoto-type transition from asynchrony to synchrony. At larger k ex, the amplitude is zero at low density and jumps sharply at higher density. (b) Comparison of simulation to experiment as k ex (or the stirring rate) is decreased and the density is held constant, following the path indicated by the white line in panel a. At the initial, high rate of exchange, neither simulation nor experiment shows any oscillations. As the rate is decreased, oscillations arise via a dynamical quorum-sensing transition and gradually desynchronize via a Kuramoto-type transition.
(Adapted from
Figure
Biological applications
The researchers hope that their study will offer insights into the dynamical nature of synchronization and quorum-sensing transitions in biological systems. In one recent study, researchers in France and Denmark found that in a stirred system of yeast cells, oscillations in the rate of a metabolic process synchronized via a dynamical quorum-sensing transition. 5 The BZ study suggests that biological systems such as stirred yeast cells might also undergo Kuramoto-type transitions, depending on the efficacy of the molecular signaling.
Showalter and colleagues have extended their study to look at catalytic particles in an unstirred solution, in which the coupling between particles is not global but local. They’ve found that spiral and bull’s-eye patterns propagate over the surface of a layer of particles, but only when the group contains more than a critical number of particles—adding or removing just a few particles is enough to turn the behavior on or off. Says Showalter, “We are excited about this because there is a striking resemblance of the grouped particles to groups of bacteria.”
References
1. A. F. Taylor et al., Science 323, 614 (2009). https://doi.org/10.1126/science.1166253
2. J. Maselko, K. Showalter, Nature 339, 609 (1989). https://doi.org/10.1038/339609a0
3. R. Toth, A. F. Taylor, M. R. Tinsley, J. Phys. Chem. B 110, 10170 (2006). https://doi.org/10.1021/jp060732z
4. A. M. Zhabotinsky et al., J. Phys. Chem. 97, 7578 (1993). https://doi.org/10.1021/j100131a030
5. S. De Monte et al., Proc. Natl. Acad. Sci. USA 104, 18377 (2007). https://doi.org/10.1073/pnas.0706089104
More about the authors
Johanna L. Miller, jmiller@aip.org




