A muscle’s mechanical advantage is not constant

Muscles pull on tendons and bones to make us move. As in any system of levers, the transformation of muscle-fiber motion into limb motion can be described by a mechanical advantage, or ratio of an output force to an input force. Muscle systems typically have mechanical advantages less than 1—they reduce forces and amplify speeds so researchers in the field of muscle mechanics work with the reciprocal quantity, the ratio of an output speed to an input speed. They call that number the gear ratio, in analogy to the gears of cars, bicycles, and other machines.

Just as a cyclist can speed up or slow down without shifting gears, a muscle with a fixed gear ratio can produce motion with a range of speeds because the muscle fibers themselves don’t always contract at the same speed. But you can achieve greater maximum speed on a bicycle by shifting to a higher gear, and you can climb steeper hills by shifting to a lower gear. Having multiple gears available increases your range of forces and speeds. Now, Emanuel Azizi and colleagues at Brown University have found, through a combination of experiments and simulations, that some muscles too can shift gears, apparently in direct response to the forces against which they act.¹

Azizi and colleagues looked at muscles that are feather-shaped, or pennate (from the same Latin root as the quill-shaped penne pasta), whose fibers are oriented at an angle to the line of motion. Arthropods’ muscles, which are confined within chitinous exoskeletons, have pennate structure, since they need to contract without bulging, as illustrated in figure 1. A possibly familiar example is a claw muscle of a crab or lobster. Vertebrates too have some pennate muscles because that arrangement fits many short muscle fibers into a long thin muscle, so that the muscle can exert greater forces than can a muscle comprising a smaller number of long fibers. The human gastrocnemius, part of the calf muscle that is responsible for lifting your whole body weight each time you take a step, is a pennate muscle.

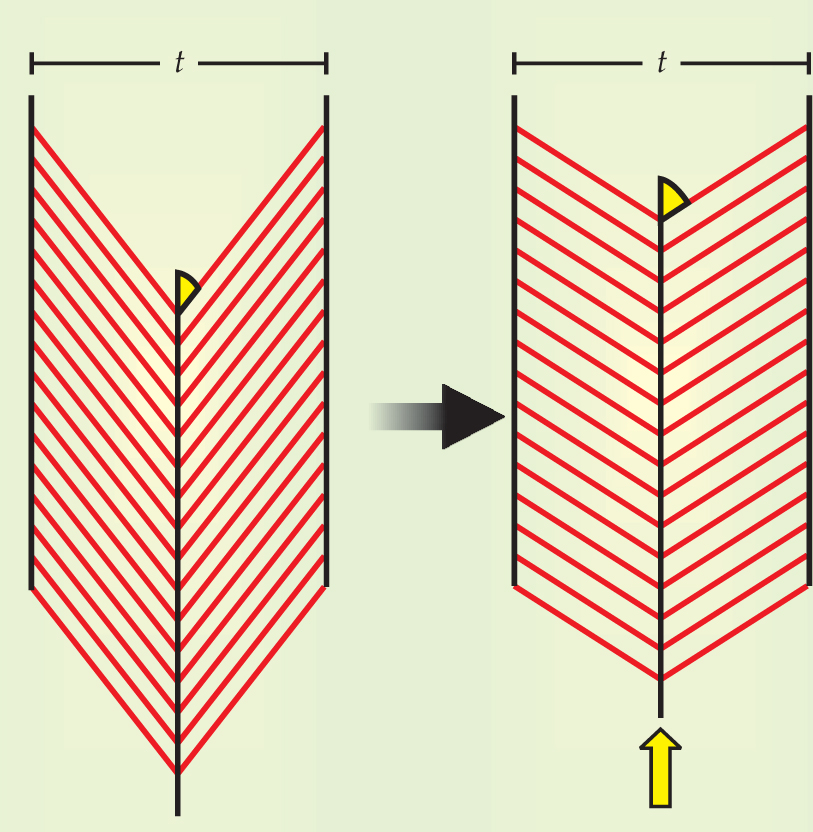
A 340-year-old model of pennate-muscle mechanics says that all pennate muscles, not just arthropods’, contract without bulging.² It’s been known for some time that the model is not always accurate, and the changes in thickness of the human gastrocnemius have been extensively quantified.³ But Azizi’s study is the first to relate a pennate muscle’s fiber structure to its shape changes and mechanical performance.

Talking turkey

Azizi and colleagues performed their experiments on wild turkeys, whose gastrocnemii, like ours, are pennate. The researchers focused on the lateral gastrocnemius, only half of the feather shape sketched in figure 1. “Quite a bit is known about the mechanical function of the turkey’s lateral gastrocnemius,” explains Azizi. “That information allowed us to integrate our isolated muscle result with in vivo behavior.”

The researchers anesthetized the turkeys, surgically accessed the nerve that controlled the muscle, and stimulated it electrically for several different resistive loads. They measured the changes in the muscle shape—fiber length, fiber angle (called the pennation angle), and muscle thickness—using piezoelectric crystals they had implanted in the muscle tissue. Since the procedure involved damaging the turkeys’ leg nerves in a way that could not be healed, all 10 of the birds they used were euthanized at the end of the experiment.

The researchers calculated the so-called architectural gear ratio, the ratio between the speed of muscle contraction and the speed of fiber contraction. According to the old model that assumes constant muscle thickness, that ratio is a simple function of the pennation angle. For a turkey’s lateral gastrocnemius, the constant-thickness model predicts an AGR of 1.2. Azizi and colleagues found that not only did the AGR differ from 1.2, but it varied based on the force against which the muscle was acting.

Figure 2 illustrates how. Compared with the relaxed configuration shown in figure 2(a), the muscle that’s contracted under a small load, as in 2b, is thicker and much shorter. The AGR for such a high-speed contraction is about 1.4. But a muscle contracting under a larger load, as in 2c, becomes thinner, doesn’t shorten as much, and has an AGR of about 1.0. The two illustrated contractions are just the two endpoints of a continuum of possibilities: Intermediate loads yield intermediate AGRs.

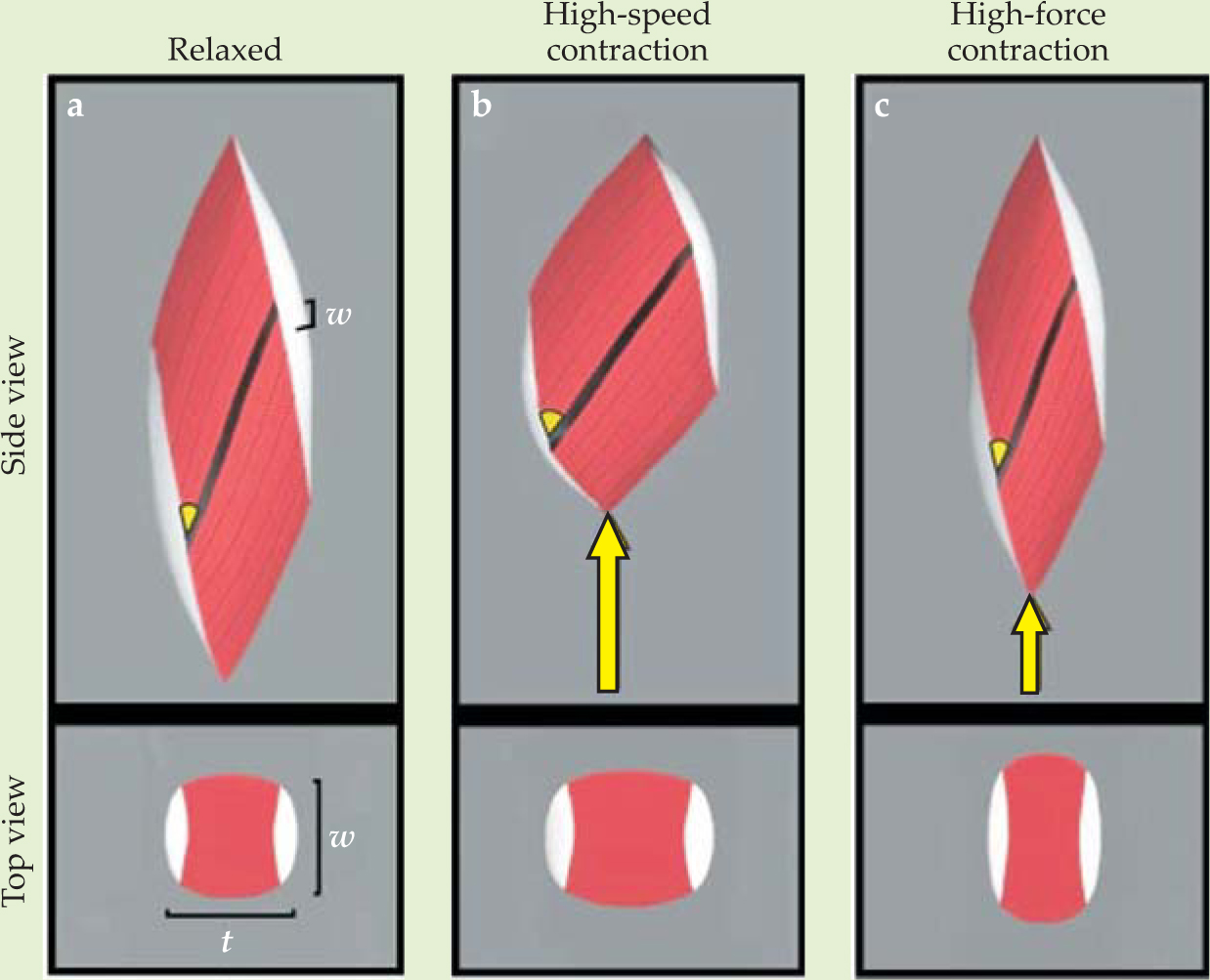
As a consequence of the variable-gearing mechanism, a greater range of forces and speeds is available to the muscle as a whole. The muscle fibers have a maximum speed at which they can shorten and a maximum force they can exert. If the AGR had a constant value of 1.2, the muscle’s shortening speed would always be 20% more than the fibers’ shortening speed, and the muscle force would always be 17% less than the total fiber force. But with the variable-gearing mechanism, the maximum muscle force is equal to the maximum total fiber force, since the AGR = 1 for high-force contractions, and the maximum muscle speed is 40% more than the maximum fiber speed, since the AGR = 1.4 for high-speed contractions.

Azizi and colleagues emphasize that the variation among the contractions is not the result of conscious or unconscious control by the nervous system, since the researchers stimulated the muscles in exactly the same way each time. Rather, it must be purely the result of forces acting on and within the muscle. Understanding the mechanics of turkey—and, by extension, human—muscles has potential applications in the design of powered prosthetic limbs, artificial muscles, and robotic systems. But also, as Lawrence Rome of the University of Pennsylvania says, “This is yet another beautiful design that has evolved but was just sitting there until someone appreciated it.”