A magnetic insulator transmits electrical signals via spin waves
DOI: 10.1063/1.3431354
Electrons carry both charge and spin as they flow in a material. For many applications, the spins are artificially polarized by magnetic fields or are naturally polarized in ferromagnets such as iron and nickel. The recent history of spintronics is rich with examples of heterostructures carefully engineered to send a current of spin-polarized electrons from a ferromagnet to metals, semiconductors, or superconductors (see the article by Jagadeesh Moodera, Guo-Xing Miao, and Tiffany Santos in Physics Today, April 2010, page 46
In fact, though, a spin current may appear wherever there is a charge current—no magnetism required. The spin polarization arises from the relativistic coupling of the electrons’ spin and orbital angular momenta. As electrons scatter from atomic impurities, they feel an effective magnetic field that alters their paths: Spin-up electrons bend in one direction, spin-down electrons in the other, both transverse to the original direction of the charge current. The transverse spin current, known as the spin Hall effect, was predicted in 1971 to exist in semiconductors but was not detected experimentally until just five years ago (see Physics Today, February 2005, page 17
A year later Eiji Saitoh (now at Tohoku University) and his Japanese colleagues discovered the inverse of the effect—the conversion of a spin current into a transverse charge current—in platinum. 1 Because both a spin Hall effect and its inverse can take place at room temperature and in metal, the researchers realized that the reciprocal conversion between spin and charge current was not a special phenomenon limited to semiconductors but could be used to integrate today’s metal-based spintronic technology with conventional electronics. Indeed, a heavy metal such as Pt exhibits a spin Hall effect far greater than that found in semiconductors such as gallium arsenide.
Saitoh, Sadamichi Maekawa (now at the Japan Atomic Energy Agency in Tokai), and their colleagues have now extended that earlier work, which was based purely on metals, to demonstrate another reciprocal effect: the interconversion of a spin current in a metal and a spin wave in an insulator. 2 The upshot is counterintuitive, at least at first glance. Although the bandgap of an insulator prevents charge conduction, it doesn’t prevent the propagation of elementary magnetic excitations called magnons, which are the quanta of a spin wave. By coupling to such excitations, an electric signal induced in the metal can be transmitted through the insulator over macroscopic distances. What’s more, because many insulators are optically transparent, the demonstration sets the stage for adapting the transport and processing of spins to photonic circuits as well as conventional electronic ones.
The diffuse and the coherent
As illustrated in figure 1, a spin current and a spin wave are different manifestations of the flow of intrinsic angular momentum J S. In a metal, the spin is typically carried by the diffusive motion of conduction electrons that scatter from impurities and atomic defects. But it can also be carried as a wave—the collective precession of stationary magnetic moments in a ferromagnet. In a thick metal film, spin waves quickly decay—typically within a micron—because of eddy currents and electron-magnon collisions. In contrast, spin waves in magnetic insulators such as certain metal oxides suffer far less damping and can travel as far as several centimeters.

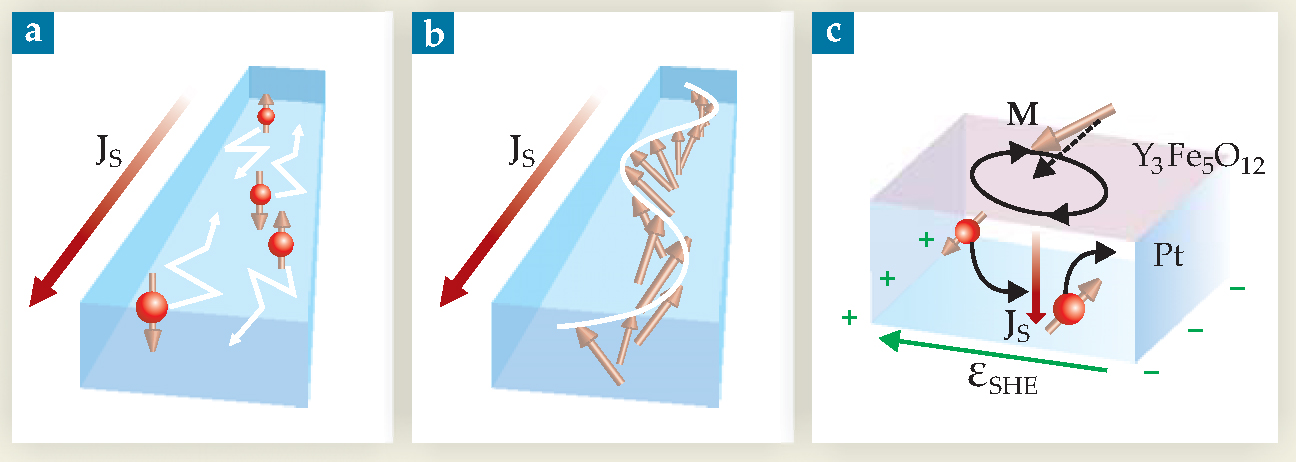
Figure 1. Spin currents in solids. Spin angular momentum J S can be carried by (a) electron diffusion or by (b) spin waves, the collective precession of magnetic moments. (c) At the interface of an insulator such as yttrium iron garnet and a metal film such as platinum, angular momentum from the precession of the insulator’s magnetization M can be pumped into the metal, where it appears as a conduction-electron spin current. By the inverse spin Hall effect, spin-orbit coupling deflects electrons of opposite spins in the same direction, whereby they accumulate on the same Pt edge. The charge imbalance sets up an electromotive force, εSHE’ measurable as a voltage.
(Adapted from ref. 2.)
That’s the reasoning behind Saitoh and company’s construction of a hetero-structure composed of a micron-thick slab of the ferromagnetic insulator yttrium iron garnet (YIG; Y3Fe5O12) that lies under two Pt strips that are separated by a millimeter. Figure 2 outlines the experimental scheme, designed to use the direct and inverse spin Hall effects to generate a spin current in the first Pt strip and then to detect it in the second.
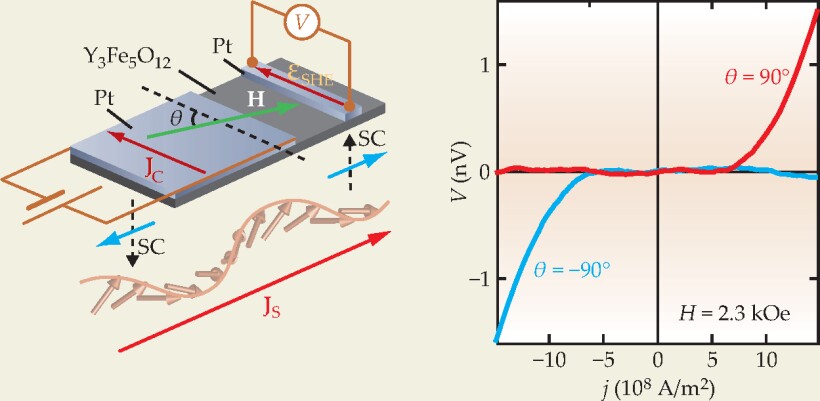
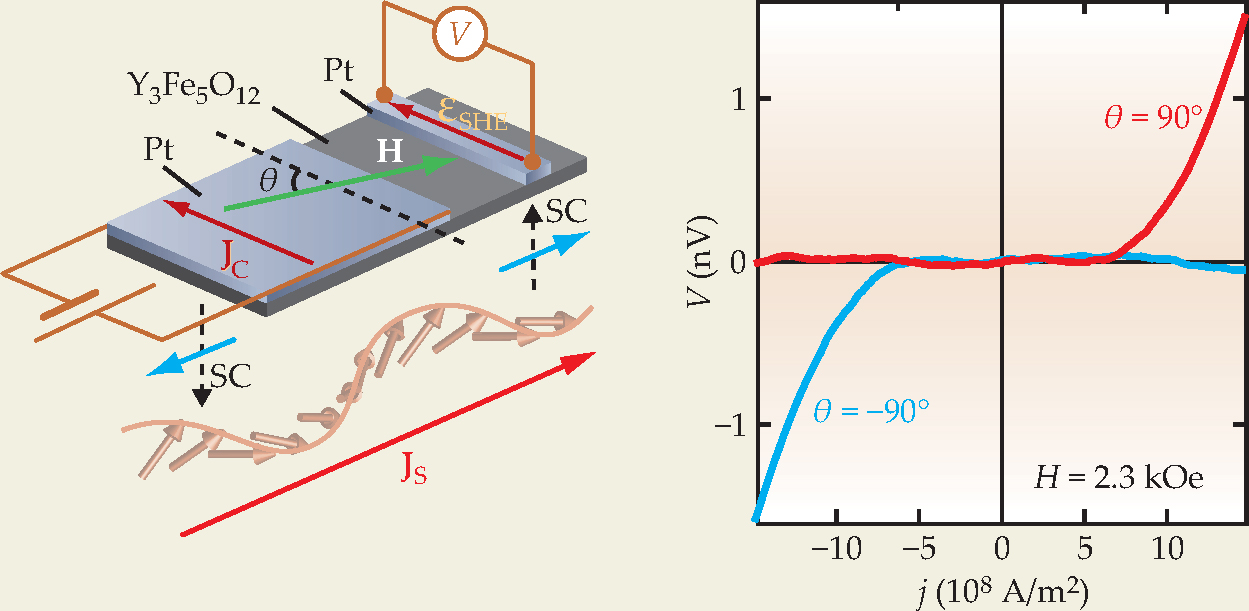
Figure 2. Electrical signal transmission. This metal-insulator heterostructure consists of two 15-nm-thick platinum films sputtered on a 1.3-µm-thick slab of yttrium iron garnet (YIG; Y3Fe5O12); the distance between the rectangular Pt films is 1 mm. A charge current J C set up by a voltage across the leftmost leads induces a downward spin current (SC) in Pt; the blue arrows indicate polarization direction. An applied magnetic field H orients the insulator’s magnetization relative to the conduction electrons’ spin polarization. When the orientation is antiparallel, a charge current density near 6 × 108 A/m2 exerts enough torque to set the magnetic moments in YIG oscillating, and the transferred angular momentum J S propagates as a spin wave. At the second Pt-YIG interface, the spin wave is transformed back to an electron-spin current, which, thanks to the inverse spin Hall effect, sets up a small but measurable voltage V. A plot of V as a function of current density j confirms the signal transmission.
(Adapted from ref. 2.)
For the spin current to be detected after crossing the 1-mm insulating gap, it must be transformed at each metal-insulator interface. A small but finite exchange interaction between Pt and YIG electron orbitals transfers angular momentum between them. As conduction electrons scatter from atoms in YIG, they exert a torque. If the current density is high enough, the spin torque can counter damping and set the moments oscillating, essentially through the quantum mechanical flipping of a spin. Downstream, the angular momentum is pumped from the spin wave back into a spin current of conduction electrons.
To test for evidence of the spin pumping at the interface, the researchers placed a rectangular YIG-Pt plate in a microwave cavity, applied a magnetic field, and measured its resonance spectra. The spin waves in YIG should be laterally quantized like the acoustic modes on a drum, they reasoned, and their recorded spectra of voltage oscillations measured as a function of field strength turned out to precisely match their spectra of absorbed microwave power as a function of field strength.
To verify that the magnetization oscillation was induced by spin torque from Pt conduction electrons, the team performed the experiment in reverse. They placed an RF antenna near the plate and looked for a microwave signal at various applied voltages. Only when the charge current in Pt reached a critical density of 4.4 × 108 A/m2—a current density consistent with their measurement in figure 2—did it induce a large enough spin current for them to see RF emission.
Could the researchers’ demonstration presage an eventual insulator-based spintronics? “That they achieved such low threshold currents in their spin-torque excitations is astonishing and certainly got my attention,” comments Thomas Silva (NIST Boulder, Colorado). By comparison, spin-torque devices used to drive the switching between random-access memory states typically require current densities three orders of magnitude higher. The Achilles heel in spintronics is usually ohmic heating from power dissipation, which increases as the square of the charge current. So lowering threshold current can really pay off.
Moreover, Silva argues, the geometry of spin Hall effects confers a practical advantage: Because spin current flows orthogonal to charge current, it’s possible to generate a total spin current much larger than the total charge current. Whereas the charge current scales as the current density times a wire’s cross section, the spin current scales as the current density times its surface area. The thinner the wire, the less ohmic heating for a given spin current density. And once the spin current is transformed to a spin wave in the insulator, Saitoh adds, the transmission generates no ohmic heating.
Although YIG has an exceptionally low spin damping—largely because it can be grown nearly defect free and generates no eddy currents—it’s unclear whether that alone can account for the low threshold current densities that are observed. Part of the mystery lies in YIG’s complex band structure and the fact that the research team had to rely on films at least a micron thick. “Thinner YIG films exhibit greater scattering and spin damping, which means researchers will have to turn to other materials to scale dimensions down,” explains Burkard Hillebrands (University of Kaiserslautern in Germany). “But that’s minor criticism. I feel sure that many groups will follow [Saitoh’s] work to optimize experimental parameters and explore more deeply the nature of the spin-wave excitations.”
It’s premature to speculate on device technologies that may emerge from the research. The transmitted signal is small: Even with 80 mA coursing through the circuit, the researchers measure an electromotive force less than a nanovolt. But the proof of principle itself plays a crucial role: By demonstrating that one can transmit a spin current into and out of a magnetic insulator, Saitoh, Maekawa, and their colleagues have opened to spintronics a rich new class of materials.
References
1. E. Saitoh et al., Appl. Phys. Lett. 88, 182509 (2006). https://doi.org/10.1063/1.2199473
2. Y. Kajiwara et al., Nature 464, 262 (2010). https://doi.org/10.1038/nature08876