A hovering resonator enhances the quantum Hall effect
DOI: 10.1063/pt.uvur.vjtr
Figure 1.
The gold square attached to the end of the copper post contains a split-ring resonator that influences the ground-state electromagnetic fields in its vicinity. By raising and lowering the resonator above a sample chip, researchers control how the sample exhibits the quantum Hall effect. (Photo by Kilian Kessler/ETH Zürich.)
The eerie music of a theremin—the instrument that’s played without touching it—seemingly comes from thin air. Eerier still is a new result from Jérôme Faist (of ETH Zürich in Switzerland) and colleagues. By holding a metallic resonator (the gold square attached to the copper post in figure
Even the darkest, emptiest vacuum isn’t devoid of electromagnetic fields. For the same reason that a particle can’t perfectly settle at the bottom of a bowl-shaped potential—because to do so would violate Heisenberg’s uncertainty principle—the energy in any of a system’s electromagnetic modes can never be exactly zero. But the set of allowed modes can be restricted through the placement of conductive materials, which impose electromagnetic boundary conditions. One manifestation of that is the Casimir effect, a measurable attraction between two conductors that stems from the diminished electromagnetic vacuum energy in the space between them (see the article by Alex Stange, David Campbell, and David Bishop, Physics Today, January 2021, page 42 ).
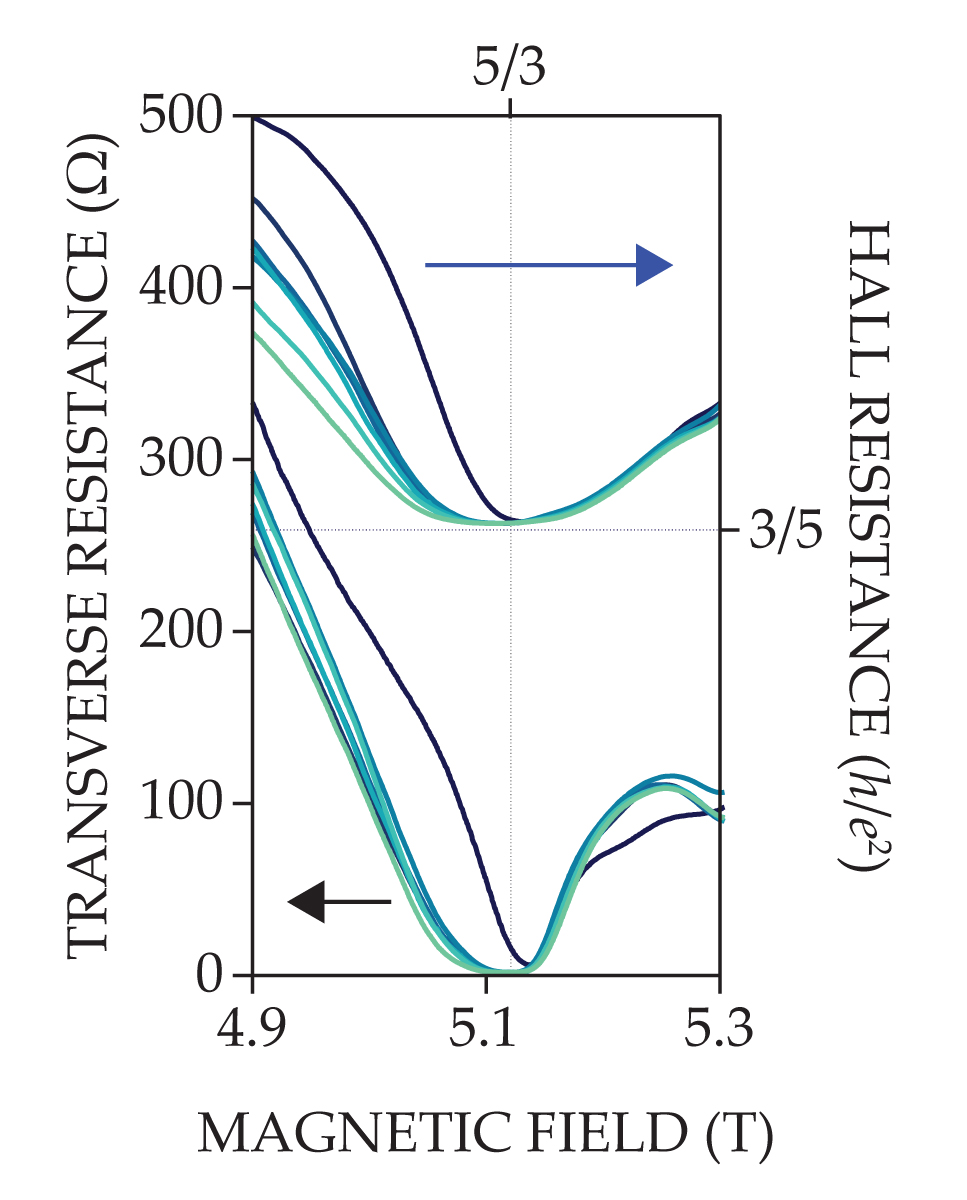
Figure 2.
The fractional quantum Hall effect is characterized by flat-bottomed curves for both the transverse and Hall resistances. When the resonator is too far from the sample to have an effect (darkest blue curves), the observed resistances barely qualify. But as the resonator is brought closer to the sample (lighter blue curves), the curves become flatter: The fractional quantum Hall effect is enhanced. (Figure adapted from J. Enkner et al., Nature 641, 884, 2025 .)
Can vacuum fields also be used to manipulate the exotic many-body states of a condensed-matter system? It should be possible, and a 20-year-old theory paper by Cristiano Ciuti (also a coauthor on Faist and company’s new paper) and colleagues drew a road map for identifying systems in which the vacuum-field energy scale could be large enough to have a measurable effect. But experimental searches have struggled until now, in part because electronic states are often probed optically, so the measurements are less sensitive to the vacuum field’s effect on the ground state. The quantum Hall effect is a fortunate alternative: It’s probed entirely through measurements of charge transport.
In the classical Hall effect, a magnetic field deflects an electric current to create a voltage perpendicular to them both; the Hall resistance—the transverse voltage divided by the current—scales linearly with the magnetic field. In the quantum Hall effect, plateaus appear at conductance values that correspond to integer multiples of e2/h, where e is the electron charge and h is Planck’s constant. In the still more exotic fractional quantum Hall effect, conductance plateaus appear at fractional multiples as well. Figure
The theory behind the enhancement mechanism, like a lot of solid-state theory, is complicated and not well understood. But there are hints of promising directions for future development. The fractional quantum Hall effect can be understood in terms of the magnetic field coupling to the electrons and forming them into quasiparticles with nonintegral charge. If the resonator’s influence is to assist with the quasiparticle formation, it’s at least plausible that manipulating the vacuum fields in other solid-state systems could help drive the assembly of other useful quasiparticles, such as the Cooper pairs that are responsible for superconductivity. (J. Enkner et al., Nature 641, 884, 2025 .)
This article was originally published online on 3 June 2025.
