A Dark-Horse Entry in the Race for an Excitonic Condensate

If electron pairs can condense into a macroscopic superconducting state, can’t electron-hole pairs—excitons—similarly condense to form a neutral superfluid? Such was the speculation of several theorists in the 1960s. Experimenters have been searching ever since for excitonic condensates. They have focused the search on the electron-hole pairs created by shining light onto a semiconductor. Such studies have turned up some intriguing behavior, but still no conclusive proof of a condensate.

The long-sought evidence for an excitonic condensate has now surfaced in a different and unexpected quarter: a quantum Hall bilayer. The bilayer is composed of two slabs of doped semiconductors separated by a thin insulating region. Each slab functions as a two-dimensional electron (or hole) gas. A strong magnetic field is applied perpendicular to the layers, and the charges move in quantized orbits about the field lines.

Because its two layers are doped with the same charge, a quantum Hall bilayer seems an unlikely place to find excitons. However, a remarkable coherence develops between the charges in the two layers when the magnetic field and the layer separation take on just the right values. In negatively doped bilayers, conduction-band electrons in one layer become acutely aware of those in the other, and they coordinate their spatial arrangement, as seen in figure 1. Each electron lines up opposite a vacancy in the conduction band—that is, a hole. These opposite charges bind as excitons that span the layers.

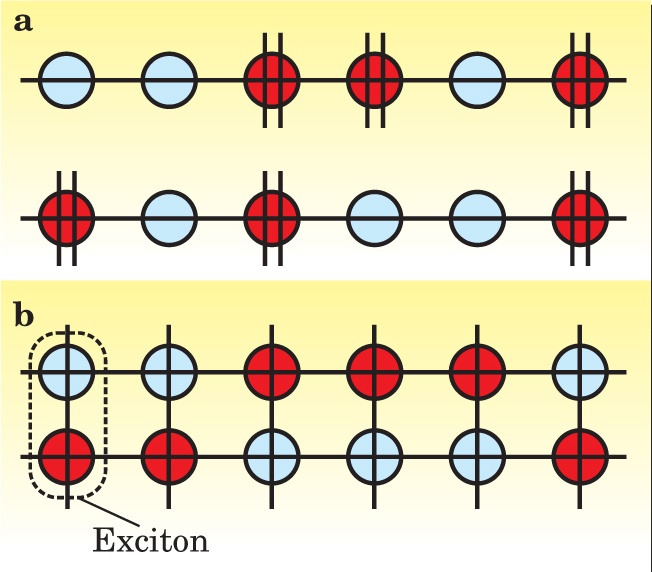
A similar pairing occurs for positively doped bilayers, but in that case, holes and electrons are both in the valence band. By contrast, the excitons created in semiconductors by photoexcitation are bound states of conduction-band electrons and valence-band holes.

The evidence for excitonic condensates comes from both electron-doped and hole-doped bilayers. The electron-doped samples were studied by Mindy Kellogg and Jim Eisenstein of Caltech together with Loren Pfeiffer and Ken West of Lucent Technologies’ Bell Labs. ² The hole-doped bilayers were probed by Emanuel Tutuc, Mansour Shayegan, and David Huse, all of Princeton University. ³

The two experiments determined both the longitudinal voltage and the transverse, or Hall, voltage when equal currents were sent in different directions through the top and bottom layers. The most dramatic result was the vanishing of the Hall voltage, which offers direct proof that excitons form and that they act as neutral particles. If electrons and holes had acted as separate particles, they would have migrated to opposite sides of the bilayer and contributed to a net Hall voltage.

The longitudinal resistance also exhibited a deep minimum. Together with the vanishing Hall voltage, the Caltech researchers assert, these data strongly suggest that the counterflowing currents are dissipationless in the limit of zero temperature. The experiments thus support the prediction that a new type of superfluid has formed.

A collective state

The sample in each of the experiments was a semiconductor structure in which two doped layers of gallium arsenide, each less than 20 nm thick, were separated by distances on the order of 10 nm by insulating layers of aluminum arsenide or aluminum gallium arsenide. The current could be injected through leads attached to the ends of both the top and bottom layers, and voltages could be measured through leads along the sides. Measurements were made at millikelvin temperatures.

These samples are far from easy to make: For more than 10 years, the Caltech–Bell Labs team has been honing the techniques needed to establish independent electrical leads and to make interlayer barriers that are sufficiently thin and yet adequately insulating.

Theorists predicted over 10 years ago that a special state would develop when the applied magnetic field corresponds to two flux quanta for each electron in a given layer—or, in the parlance of the quantum Hall system, when the filling factor ν (the ratio of electrons to magnetic flux quanta) in each layer is 1/2 (see Physics Today, May 2001, page 14 ). For large layer spacing, electrons in one layer are oblivious to the charges in the other, as sketched in figure 1.

When the layers are close enough, the charges in each layer feel one another’s presence and act as if they are all in the same layer. The charge carriers then can’t tell which layer they are in. The separate ν = 1/2 states behave collectively as a single ν = 1 quantum Hall state. Each electron always positions itself opposite an empty state in the other layer. Such electron–hole pairs are the excitons in this system.

In 1992, theorists Xiao-Gang Wen (MIT) and Anthony Zee (University of California, Santa Barbara) pointed out that excitons in the ν = 1 bilayer always form a condensed state. ⁴ That’s in contrast to the more conventional, photoinduced excitons in semiconductors, which exist as independent entities at temperatures above those at which they are expected to condense. Wen is excited about the recent experiments. “A superfluid in a fractional quantum Hall system,” he exclaimed. “This is quite amazing.”

Wen and Zee predicted that quantum Hall excitons should have all the properties of a neutral superfluid. One such property is the vanishing resistance in a counterflow experiment, which the new experiments have seen. Among the other properties is the zero-bias tunneling of current across an insulating junction separating two superconductors.

Four years ago, Ian Spielman and the rest of the Caltech–Bell Labs team saw the tunneling peak in essentially the same quantum Hall bilayer as the one used in the recent experiment. The group found that the interlayer tunneling current, which is normally strongly suppressed, developed an enormous and narrow peak when the voltage difference approached zero. ⁵ The enhanced tunneling signals strong coherence among excitons.

Vanishing resistances

In the recently published experiments, the Caltech–Bell Labs and Princeton groups independently measured the Hall and longitudinal voltages when equal but opposite currents flowed in the two layers. To find the corresponding resistances, they divided by the current in a given layer. The teams compared such counterflow measurements to those made when the top and bottom currents flowed in the same direction.

As shown in figure 2, the Hall resistivity for parallel current flow in the closely spaced bilayers exhibits the characteristic Hall plateaus at integer values of filling factor. (These integer values occur at magnetic field values denoted by arrows). With counterflowing currents, the Hall resistivity looks much the same—except at ν = 1, where the resistivity heads to zero. This behavior shows that the current is being transported by neutral carriers.

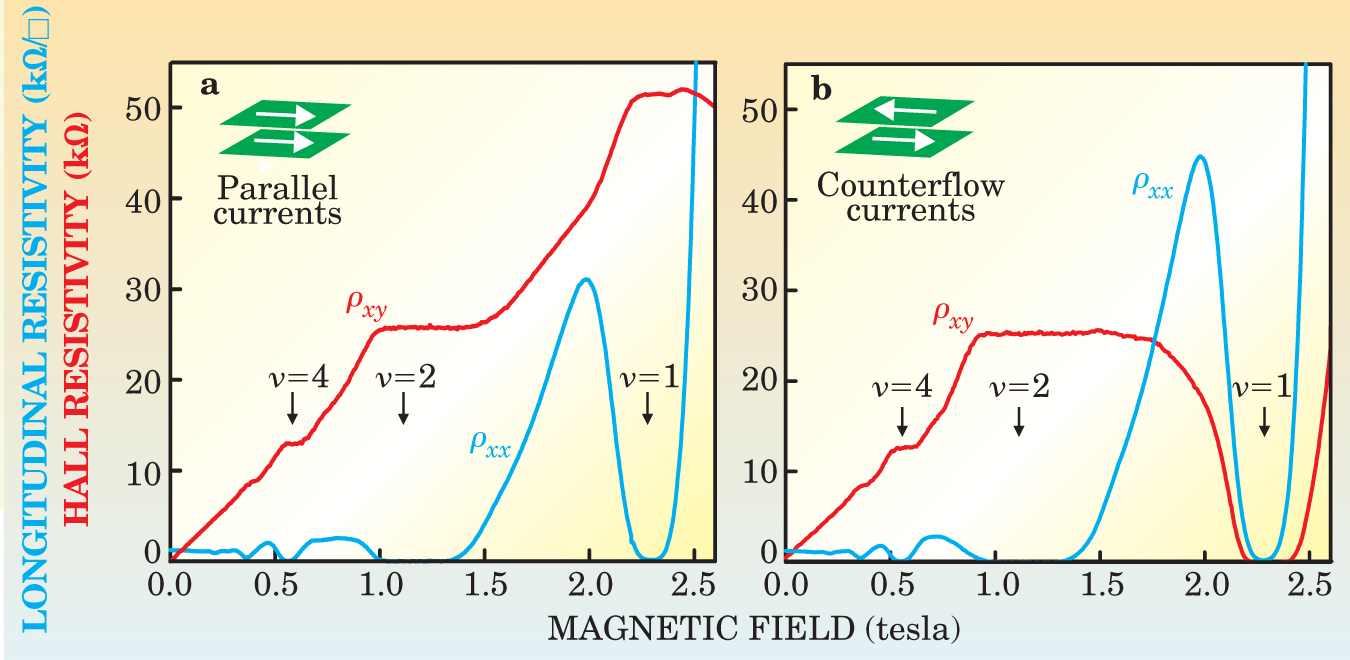
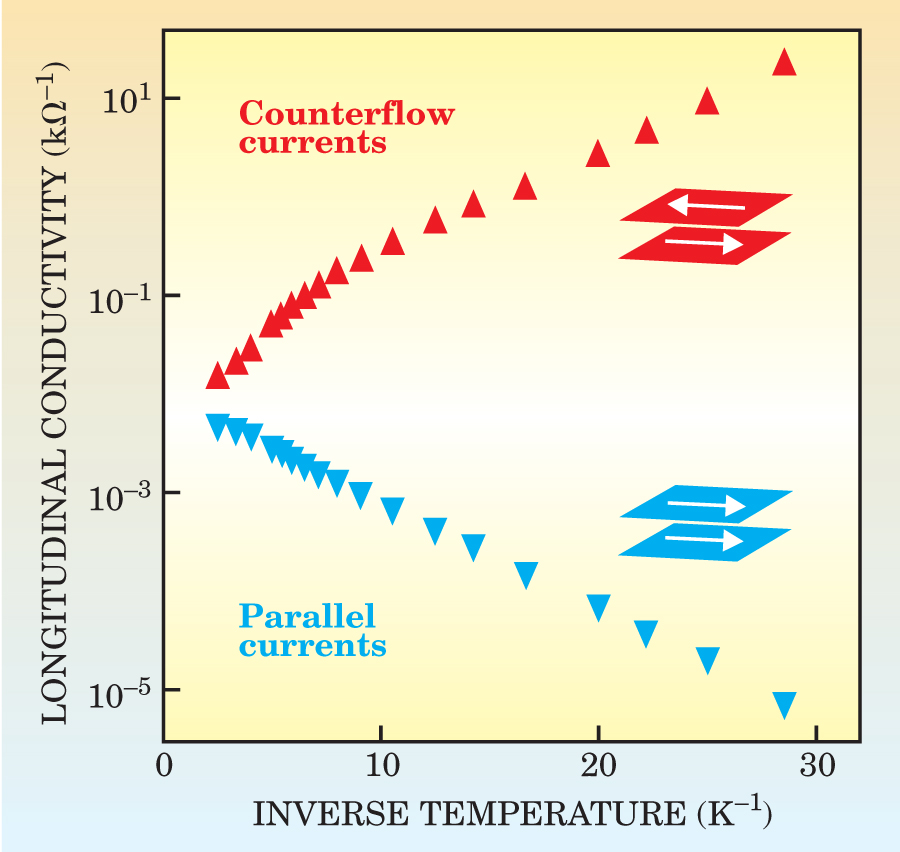
The longitudinal resistivity drops toward zero at ν = 1 for both parallel and counterflowing currents. But the conductivity tells a different story. That’s because the longitudinal conductivity is not simply the reciprocal of the longitudinal resistivity but also involves the Hall resistivity. In the case of parallel currents, one expects the conductivity to drop to zero because of the large Hall resistance. For the counterflow case, however, the longitudinal conductivity should be infinite if the excitons have formed a superfluid. As seen in figure 3, the recent experiments found that the longitudinal conductivity for the counterflowing currents grew very large with decreasing temperature—many orders of magnitude larger than the conductivity for the parallel currents. The conductivity, however, remained finite.

Strictly speaking, one cannot have a condensate in two dimensions because there is no true long-range order. The closest one can get is to enter a condensate-like phase described in 1973 by Michael Kosterlitz and David Thouless. ⁶ Below a certain temperature now known as the Kosterlitz–Thouless (KT) temperature, the system should consist of pairs of vortices of opposite rotation. The transition into that state should be signaled, says theorist Steve Girvin of Yale University, by a change in the dependence of the resistivity on the current. The recent measurements are not consistent with the KT predictions.

Both Shayegan and Eisenstein say that disorder in their respective systems is the most likely explanation for both the finite conductivity and the deviation of the low-temperature behavior from KT predictions. They and their colleagues are working to further reduce the disorder.

Shayegan notes that the key observation is that the counterflow Hall resistivity approaches zero as the temperature goes to zero. From that, he says, one can conclude that the T = 0 ground state is a superfluid.

Sankar Das Sarma of the University of Maryland, College Park, comments that the recent experiments have demonstrated an excitonic condensate but not necessarily a superfluid. He thinks that the strong disorder has suppressed the superfluidity in the system and perhaps lowered the KT temperature all the way to zero. To his mind, the system is more like a Bose glass of exciton condensate with no long-range superfluid order.

For his part, Eisenstein asserts that the counterflow results demonstrate that excitons are not only present but have a conductivity that grows rapidly as the temperature is reduced. Although the conductivity is finite at all finite temperatures, he says, it does appear to diverge as the temperature heads toward absolute zero. By contrast, the diffusion constant of electrons of an ordinary metal saturates at low temperature. In the opinion of Allan MacDonald of the University of Texas at Austin, the longitudinal conductivity (and the exciton diffusion constant) seen in the ν = 1 quantum Hall bilayers is highly unusual, and it provides strong evidence for the basic theoretical prediction of excitonic superfluidity in an ideal, disorder-free system. Theorists and experimentalists alike are still challenged to learn just how disorder limits the conductivity in real samples.

Conventional excitons

Other researchers are actively pursuing signs of a condensate of excitons that have been photoinduced in more conventional semiconductor systems. Unfortunately, the experiments have been hindered by the short time the excitons live before the electrons and holes recombine: Too often, the charges annihilate before they can cool down to the temperatures at which they might condense. In recent years, researchers have cleverly skirted that limitation by forming the excitons in coupled quantum wells so that electrons and holes are spatially separated in adjacent wells. Experiments have now attained lifetimes for such “indirect excitons” on the order of microseconds, much longer than the typical thermalization times.

Experiments to date have accumulated some evidence for condensation of indirect excitons. It includes enhanced exciton mobility, large fluctuations in exciton emission suggestive of proximity to a phase transition, and a strong amplification of the radiative decay rate.

Two years ago, two research collaborations reported photoluminescence characteristic of exciton emission that occurred in a circle some distance from where a laser had initially formed excitons. At first, researchers thought the bright ring might be attributed to condensate formation, but the ring has since been explained away as the boundary between spatially separated regions of charge. ^7,8 Leonid Butov of the University of California, San Diego, and his collaborators find, however, that the photoluminescence ring is fragmenting into a periodic array of aggregates, and they speculate that the fragmentation may be a sign of collective behavior.