A complex symmetry arises at a spin chain’s quantum critical point

In one dimension, the Ising model consists simply of a line of spins with nearest-neighbor interactions that tend to align the spins spontaneously in a ferromagnetic order. The one-dimensional model readily yields an exact solution, and the system has no phase transition at finite temperatures. The Ising model for a 2D array of spins is far more challenging, and its theoretical description, which includes a second-order phase transition, leads to far richer physics. The 1944 work that Lars Onsager did on the 2D Ising model paved the way for the subsequent study of critical phenomena that occur at phase transitions.

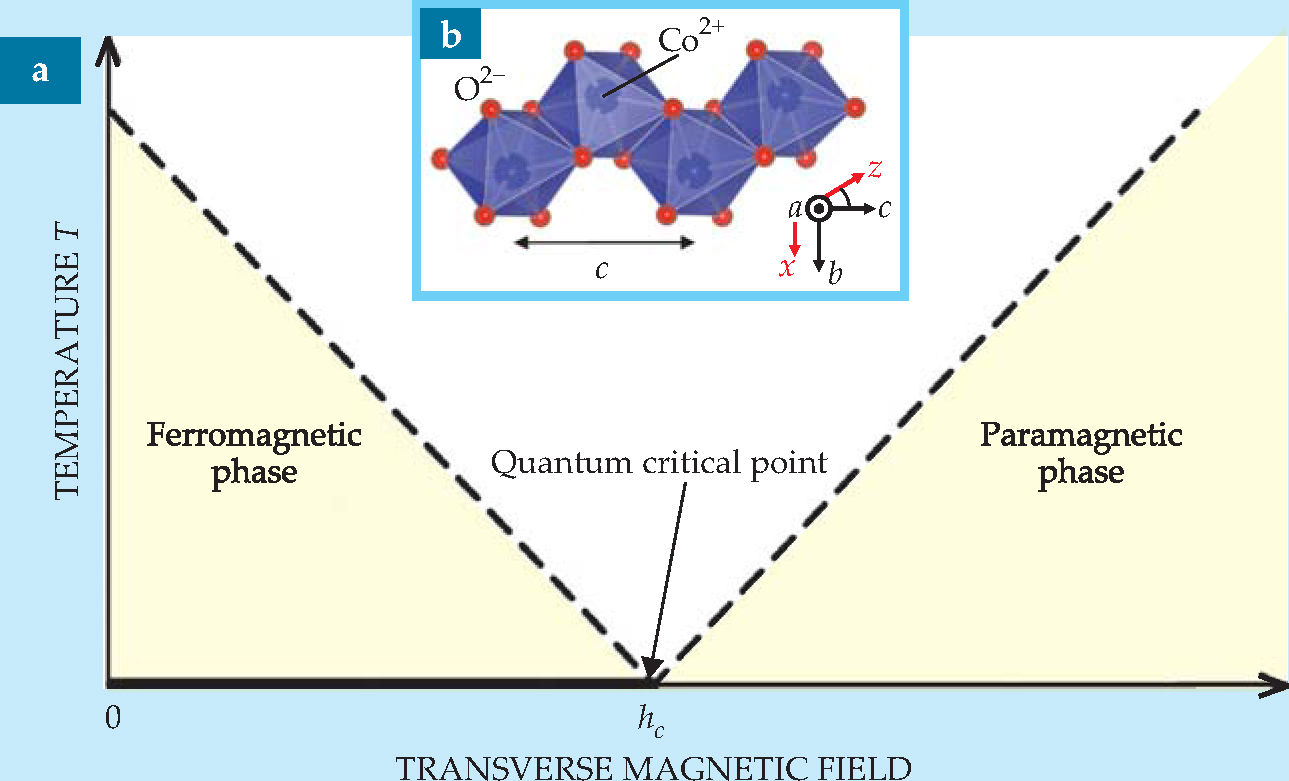
Many decades later, the Ising model retains its interest for studies of critical phenomena, but such studies are now largely focused on quantum critical points (QCPs), where phase transitions occur at a temperature of absolute zero. For example, as shown in figure 1(a), the 1D Ising chain, when placed in a magnetic field at right angles to the natural direction of spin alignment, has a phase transition at T = 0 from a ferromagnetic phase, with spins spontaneously aligned, to a paramagnetic phase, with spins rotated in the direction of the applied field. ¹

At a QCP, the system is governed by quantum rather than thermal fluctuations. Just like the thermal fluctuations in a classical phase transition, the quantum fluctuations melt the ordered phases and destroy any preference of the system for one type of order over another. The correlation lengths, or measures of the system coherence, go to infinity, and the system looks the same on all length and time scales. Those divergent length scales, says theorist Shou-Cheng Zhang (Stanford University), wipe out the geometrical differences and allow the emergence of higher symmetries. Theorists want to learn about the nature of such emergent symmetries because, even away from the QCP, they influence the system and the interplay between its competing phases.

Twenty years ago theorist Alexander Zamolodchikov (now at Rutgers University) discovered that a very complex symmetry—known as the exceptional Lie group E ₈—emerges at the QCP of the quantum 1D Ising chain. ² String theorists had known about E ₈, which plays a big role in heterotic strings in particular, but they were surprised to see it emerge in a condensed-matter system. The E ₈ group has a complex mathematical structure, but it can be interpreted physically as a theory for a group of eight particles, described by eight quantum numbers. Those particles correspond to the collective spin excitations, or quasiparticles, in the Ising model.

Zamolodchikov’s solution is the most complicated integrable model known, says Subir Sachdev of Harvard University. No one expected to see E ₈ emerge from it. It’s especially amazing, he adds, that one can check it with an experiment. Indeed, only recently could researchers reach the high fields and low temperatures needed to access the critical point and have high enough instrumental resolution to resolve the masses of at least some of the quasiparticles they excited. (Temperatures have to be low enough to suppress any impact of thermal fluctuations.)

A team led by Radu Coldea of the University of Oxford has now validated the E ₈ prediction in a neutron-scattering experiment on a crystal that contains rows of atomic spins. ³ The team was able to discern the masses of the two lowest-energy quasiparticles and found that as the Ising system neared its QCP, the mass ratio approached that expected for the two lowest masses of the E ₈ group.

Leon Balents (University of California, Santa Barbara) comments that the Ising model is the canonical theoretical example of a quantum critical point, and one of the most nontrivial. It’s also one about which much is known, thanks to Zamolodchikov’s work. “It’s rare,” Balents adds, “to know the full spectrum of particles in the vicinity of a QCP.” The results give hope to theorists like Piers Coleman of Rutgers University that higher mathematics can lend insight into more challenging condensed-matter systems. As an example, Coleman cites metallic systems, in which the interplay of the magnetism with charge leads to new kinds of excitations that we don’t fully understand.

Phases of the Ising chain

Picture a row of spins S that tend to align spontaneously along some preferred direction z, and you have the quantum 1D Ising model. Quantitatively, the interaction between neighboring spins S_z at sites i and j is given by —JSⁱ _zSⁱ _z, where J is the ferromagnetic coupling strength. When a magnetic field h_x is applied in a transverse direction x perpendicular to z, the field competes with the spontaneous ordering and, at high enough values, forces the spins to line up along the x direction. At absolute zero, the transition between the low-field ferromagnetic state and the high-field paramagnetic state occurs right at a critical value h _c that’s proportional to the coupling strength J.

To realize an Ising chain experimentally, Coldea and his team used a large crystal of cobalt niobium oxide (CoNb₂O₆), as shown in figure 1(b). Cobalt atoms behave as effective spin- $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ particles, arranged in a zigzag fashion along the crystal’s c axis. Each Co chain is only weakly coupled to its neighbors, so it can be treated effectively as being 1D. The direction of spin alignment z is in the crystal’s ac plane and the transverse field h_x is applied parallel to the crystal’s b axis. The exchange interaction J is particularly small in CoNb₂O₆, so that the QCP lies at h _c = 5.5 T, a field that is attainable by experiment.

The researchers hail from the University of Oxford, the Helmholtz Center Berlin for Materials and Energy, the University of Bristol, and the Rutherford Appleton Laboratory near Oxford. To create the E ₈ quasiparticles, they excited the spin chain by inelastic spin-flip scattering of neutrons from the Rutherford Appleton Lab’s ISIS pulsed neutron spallation source. At transverse fields below the QCP, each neutron flips one of the spins in the chain, as shown in figure 2(a). Flipping a spin is equivalent to creating two domain walls, or kinks, each separating a ground-state region with spins up from one with spins down. The kinks can move away from one another, as shown.

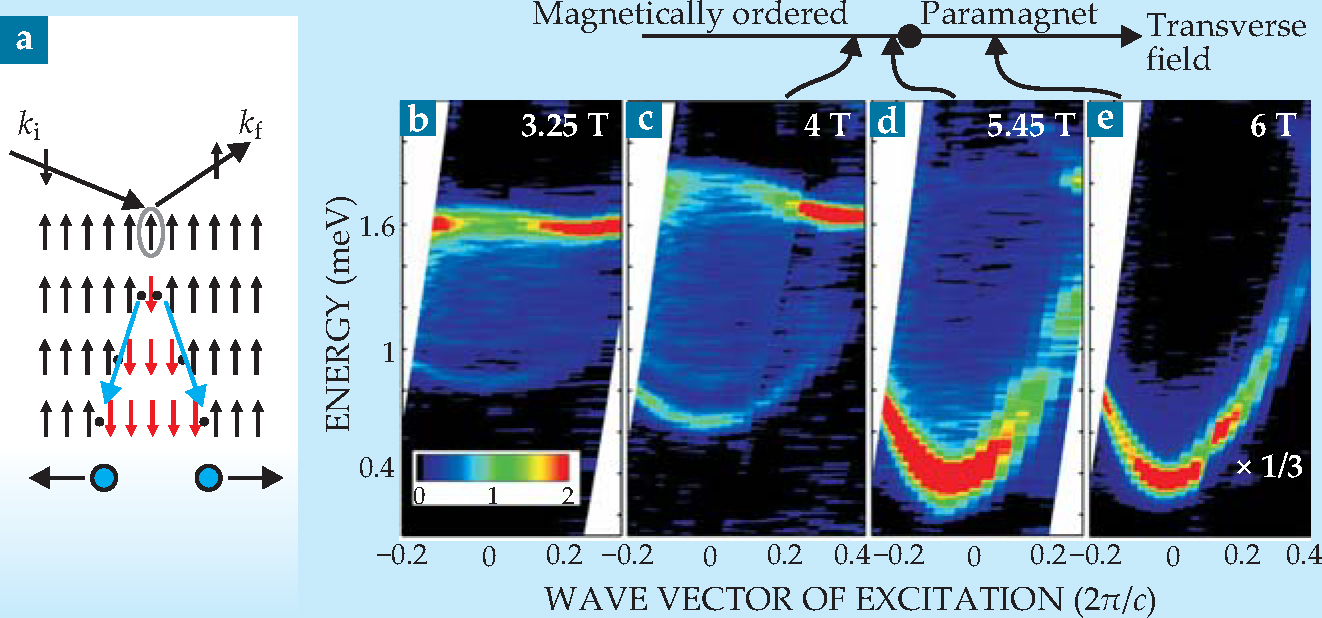
At values of the transverse field above the QCP, the system is no longer ferromagnetic but paramagnetic. In that region, neutron scattering also flips a spin. However, the excitation can’t be split into two domain walls because the system has only one ground state, which has spins aligned along the applied field. The flipped spin can move to neighboring sites, but it moves as a single entity.

The basic excitations produced by neutron scattering in the two phases produce unique signatures in the graphs of energy versus momentum that Coldea and his colleagues measured, as shown in figures 2(b)–2(e). Below the QCP, the continuum response seen in the experimentally measured scattering reflects the different ways in which the kinks can share the momentum and energy. The bottom of the blue shaded region resembles the quadratic dispersion curve that a single kink might have. The spread of energy is the widest when the total wave vector L for the kink pair is zero—that is, when the kinks are moving away in opposite directions with equal momentum. When L > 0, the kinks share the momentum unequally, and the energy spread is smaller. (The red areas near the highest energies have to do with kinetically bound kink pairs, which travel in the same direction.)

Above h _c, the phase space diagram is easier to understand. The system has only one quasiparticle, the flipped spin, and it has the quadratic dispersion seen in figure 2(e). Close to h _c (figure 2(d)), both the continuum and discrete spectra appear, merging with one another.

A small perturbation

Where are the eight particles predicted by the E ₈ symmetry? That symmetry was expected to emerge at the QCP of a 1D quantum Ising chain when the chain was subjected to a small longitudinal field in addition to the transverse field, whose purpose is to put the system at or near a QCP. An additional longitudinal field is needed to match the experimental system to the problem solved by Zamolodchikov. Fortuitously, the 1D Ising chain in the CoNb₂O₆ crystal naturally feels a small additional longitudinal magnetic field that stems from the weak coupling between adjacent Co chains in the crystal structure.

Strictly speaking, right at the QCP, the quantum critical state should have a gapless continuum of states. Away from the QCP, a low-energy scale emerges, and the system can no longer be described by a conformal, or scale-invariant, theory. Amazingly enough, however, the signature of the E ₈ Lie group emerges in the 1D Ising chain even with the longitudinal field perturbation. As Zamolodchikov explains, it’s like inferring the intricate symmetric patterns of a room full of dancers by studying their shadows along the wall. The shadows don’t have the same symmetry as the dance but they inherit some properties from the symmetry.

The impact of the small longitudinal field is to produce bound states of the kinks. Even in the absence of a transverse magnetic field, neutron scattering produces pairs of kinks. With a longitudinal field present, however, the motion of the kinks affects the interactions with the neighboring chains. If the kinks move apart from one another, the domain between them grows. Because of the couplings between adjacent chains, it costs more energy to create a larger domain. That energy penalty creates a kind of string tension between the kinks that resists their separation. The result of that “kink confinement” is to produce discrete bound states of the pairs of kinks.

In theory, the system has a large number of kink bound states. With the transverse field set to zero and with the crystal at very low temperatures, Coldea and his group were able to see up to five of the discrete bound kink states predicted by kink confinement, as shown in figures 3(a) and 3(b). Similar arrays of discrete states, sometimes called Zeeman ladders, have been seen in other systems, most notably in experiments on Ising-like antiferromagnetic compounds. ^{4 , 5} Steve Nagler of Oak Ridge National Laboratory, who was involved in those earlier experiments, notes that the new contribution by the Oxford group is that they can take their system all the way to the QCP.

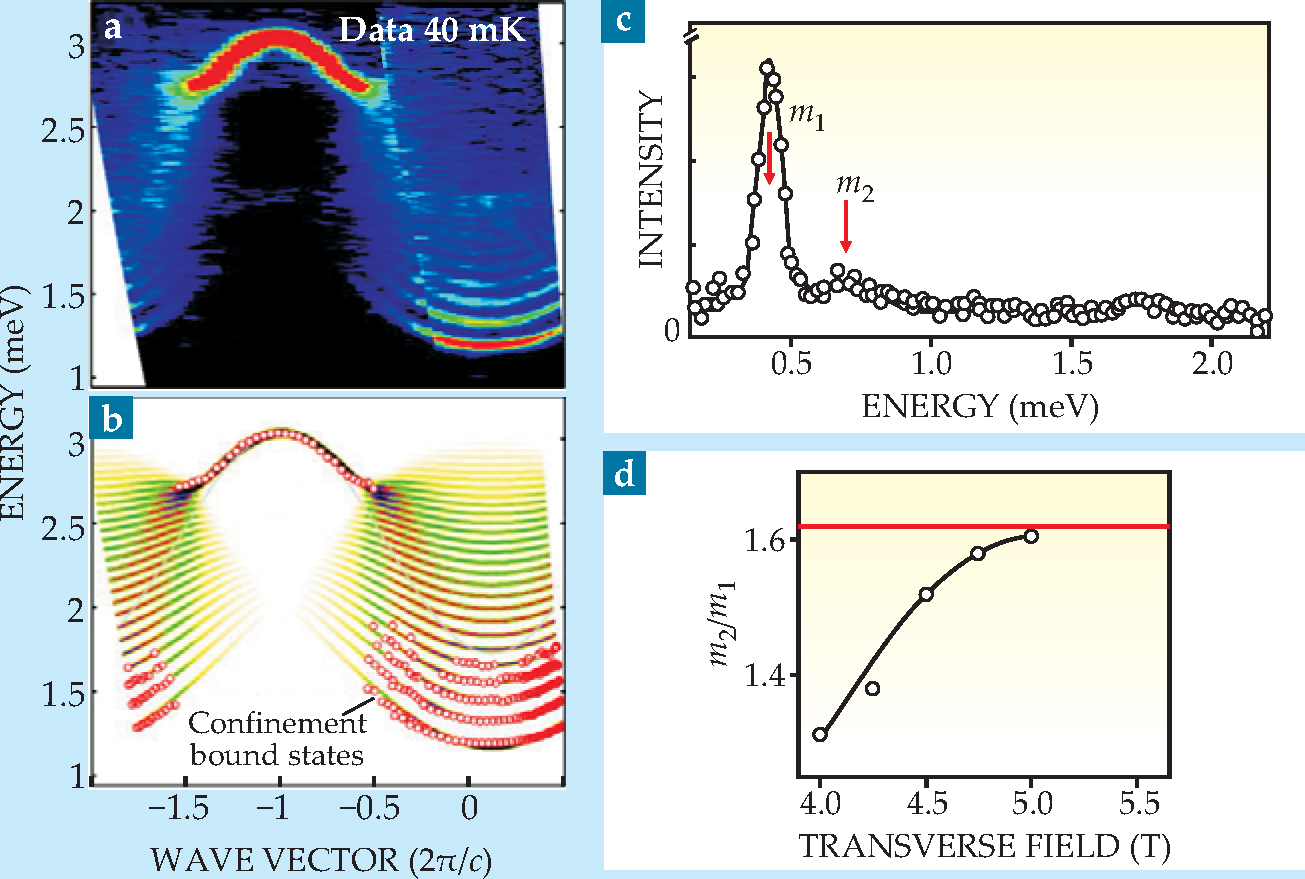
Coldea and his colleagues studied how the discrete states evolved as the transverse field approached h _c. At each field value, the experimenters extracted the energies, or masses, of the kink bound states (figure 3(c)). It’s expected that all but the eight lowest energy states become unstable and decay as the system approaches the QCP. At field values close to the QCP, the experimenters could resolve two mass peaks. They plotted the ratio of those two masses as a function of the transverse field value, as seen in figure 3(d). The ratio approaches the golden mean value of (1+√5)/2. That’s exactly the ratio of the lowest two masses as predicted by E ₈ group theory.

Seeing all eight of the masses predicted by the emergent E ₈ symmetry is beyond current experimental capabilities. Just to resolve the lowest two masses in the recent experiment required a very high resolution time-of-flight instrument. Even higher-resolution time-of-flight instruments are being built, says Coldea, one of them at ISIS. He hopes to be able to see the third and possibly higher E ₈ masses in future experiments.