The first wetting layer on a solid
DOI: 10.1063/1.3326987
Water is everywhere, the stuff of life, sculptor of the natural environment, helper and headache in a wide range of technologies. The first layer of water molecules at a surface is the structural template that guides the growth of ice, embodies the boundary condition for water transport, and mediates aqueous interfacial chemistry. It thus determines if rain will fall, how fast pollutants migrate in rock and soil, and governs corrosion, catalysis, and countless other processes.
This article is a report on recent efforts to understand water on surfaces that, by virtue of a stronger affinity for water than water has for itself, support a two-dimensional wetting layer. Such surfaces are said to wet completely. 1
The interaction of waxy or oily (hydrophobic) surfaces with adjacent water is weakly attractive at best. Thus, to a first approximation, water on hydrophobic surfaces is water in equilibrium with its vapor, a problem whose narrow range of outcomes is governed by surface topography and dielectric behavior—that is, macroscopic considerations. At complete-wetting surfaces, conversely, the water molecules’ arrangements, dynamical behavior, and roles in interfacial chemistry are largely contingent on atomic-scale surface structure and composition. And understanding them presents serious challenges to the experimental and theoretical state of the art.
Spectroscopy, high-resolution imaging, and the scattering of x rays or electrons can reveal important structural clues, provided the experiments don’t alter the typically delicate sample. But filling in the atomic-level details theoretically is fraught with difficulty, attributable to force laws of questionable accuracy (whether semiempirical or ab initio), energy surfaces with many relative minima and many barriers, and the quantum nature of the proton—that is, the effects of proton zero-point motion and tunneling.
Still, deciphering the details was not expected to be so challenging, at least not for water on the hexagonal surface of a precious metal. For some two decades researchers imagined that in that ideal case, water molecules would initially arrange themselves as one hexagonal layer of the naturally occurring ice crystal, “ice Ih,” which conserves hydrogen bonds by straining to fit the metal lattice constant. But 21st century work on water adsorption, both theoretical and experimental, has consistently called into question whether an icelike wetting layer ever exists (see
Even the most basic question about complete wetting—why a particular surface is more attractive to water than water is to itself—can be hard to answer. Is the observation of a 2D water layer the result of kinetic hindrance—that is, a dewetting barrier—or of thermodynamics? If kinetics is at stake, then total energy minimization is a structural tool of questionable value, whether or not a reliable force law is available. Is the formation of hydrogen bonds between a water layer and a solid sufficient to make complete wetting thermodynamically favorable? When is surface chemistry—for example, the transfer of hydrogen atoms from water molecules to surface sites or surface impurities—at the heart of wetting?
Learning the structure of the first layer of water molecules on a solid is not an end in itself but preliminary to understanding multilayers. With that in mind, two novel studies give one pause. 2 , 3 The first water layer on the close-packed surface of platinum, the studies agree, is hydrophobic to succeeding ones. That poses unexpected questions for ice epitaxy and for water transport. For example, on what wetting surfaces should epitaxy occur? And is a “no slip” boundary condition appropriate for transport along the surface? The same questions arise for water on kaolinite, a clay thought to seed ice nucleation in clouds. The first water layer on that oxide has been predicted to grow two-dimensionally—but once again in a way that seems to render the surface hydrophobic to subsequent water. 4
Structure of ice
Victor Petrenko and Robert Whit-worth’s Physics of Ice (Oxford University Press, 1999) provides a comprehensive review of the structure and properties of ice. The atomic arrangement of the defect-free, naturally occurring ice crystal (ice Ih) minimizes electron-electron repulsion in a tetrahedrally bonded, hexagonal-close-packed “wurtzite” structure. Thanks to tetrahedral bonding, the crystal forms a stack of bilayers, represented here schematically. Each oxygen atom in a bilayer forms hydrogen bonds with three nearest neighbors in a plane 0.92 Å below it, and a fourth with an equidistant O atom 2.76 Å above in the neighboring bilayer.
For two decades it was assumed that the first wetting layer on a hexagonal crystal face would be a single, icelike bilayer. First-principles calculations, however, imply that a nontetrahedrally bonded first water layer is energetically preferable. This was initially something of a surprise, but it should not be, given that complete wetting means water molecules have a stronger affinity for a surface than for each other.
Water on metals
But for the occasional nugget, metals are not part of our daily experience of nature. More stable materials such as oxides, sulfides, and salts are. So why have most molecular-level studies of wetting referred to metals nonetheless—and at low temperatures in ultrahigh vacuum (UHV)? It’s not that metals conduct electrons or that applications like corrosion, fuel cells, and electrocatalysis are any more important than rainfall, erosion, or transport of toxic materials in soil. Rather, metals represent the simplest test bed for refining understanding.
We know how to prepare and clean nearly perfect, single-crystal (particularly, precious) metal surfaces in UHV, and a wide variety of surface science techniques, many of which do require electrical conductivity, are available to study them—with and without water present. Years of such studies have produced a large database. 5 , 6 About a dozen wetting systems, including water on nine different metal surfaces, are known from diffraction experiments to be ordered and thus more susceptible to analysis. 6 Scanning tunneling microscopy (STM) images of adsorbed water are available for several metal-crystal faces, and some cases—for example, a recent study of water on the (110) surface of copper 7 —allow conclusions to be drawn from theoretical image simulation.
There are also telling spectroscopic experiments—for example, x-ray photoelectron spectroscopy, which easily distinguishes dissociative from nondissociative adsorption, and IR absorption, which in addition provides information on bond orientation.
The classic bilayer
Given that the naturally occurring ice crystal is hexagonal with a lattice constant of 4.5 Å, close to

Figure 1. The classic hexagonal bilayer on a five-layer ruthenium slab. Large, medium, and small balls represent Ru, oxygen, and hydrogen atoms. The O atoms of the flat-lying water molecules each lie 2.5 Å directly above a Ru atom. The O atoms of the remaining water molecules lie 0.8 Å higher. The green arrow indicates a dangling O-H bond, which largely consumes the power of the oxygen 2pz orbital to form a bond.
(Adapted from ref. 8.)
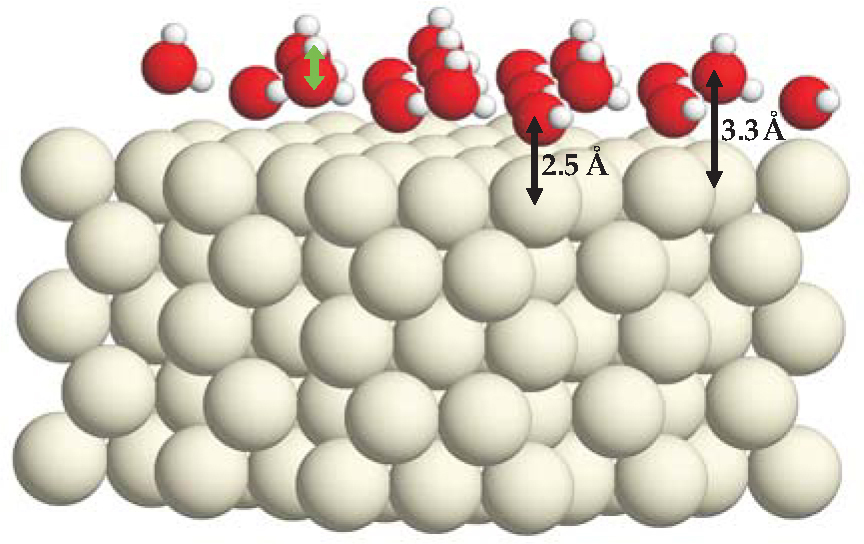
Though it has been a paradigm for decades, definitive evidence for the puckered bilayer remains to be uncovered. Indeed, much recent progress in understanding wetting has been the result of challenging the classic model. One contentious question has been whether wetting-layer water molecules remain intact.
Are the water molecules intact?
In their 1987 review, Patricia Thiel and Theodore Madey suggested that dissociative adsorption of an H2O molecule as OH and H fragments is unfavorable on all the precious metals—with ruthenium and osmium being borderline cases. 5 Seven years later Georg Held and Dietrich Menzel published a low-energy electron-diffraction study of a periodic D2O layer on the hexagonal face of Ru, yielding what was, for years, the only quantitative structural information for water on a surface. Importantly, Held and Menzel found that the heavy-water layer’s O atoms were virtually coplanar, confounding expectations based on the classic bilayer.
To explain coplanarity, a new idea was needed. After eight more years, a successful one emerged: 8 In the classic bilayer, there is no driving force to move an upper O atom toward the surface, because an upper O atom’s power to bind to the metal is consumed in forming its dangling O-D bond. Were that bond broken, the upper O atom would move down.
First-principles calculations supported that elementary chemical notion. Optimization of a water adlayer, with dangling O-D bonds replaced by Ru-D bonds, yielded a nearly coplanar O structure (see figure 2), bound at least 0.2 eV per D2O molecule better than the paradigmatic bilayer. Zero-point motion, which favors breaking stiff O-D bonds, adds to the binding of the partly dissociated water layer and makes it thermodynamically favorable compared with a nonwetting arrangement of 3D ice droplets on the 100- to 120-K surface.

Figure 2. A half-dissociated layer of water molecules on the close-packed surface of ruthenium, seen from side and oblique perspectives. The upper panel shows that the oxygen atoms (red) are almost coplanar. The lower panel shows that there are just enough metal-atom surface sites to accommodate the hydrogen atoms (small, white) dissociated from half the water molecules. Strong bonds between OH and Ru have pulled all O atoms closer to the metal than they were in the arrangement pictured in figure
(Adapted from ref. 8.)
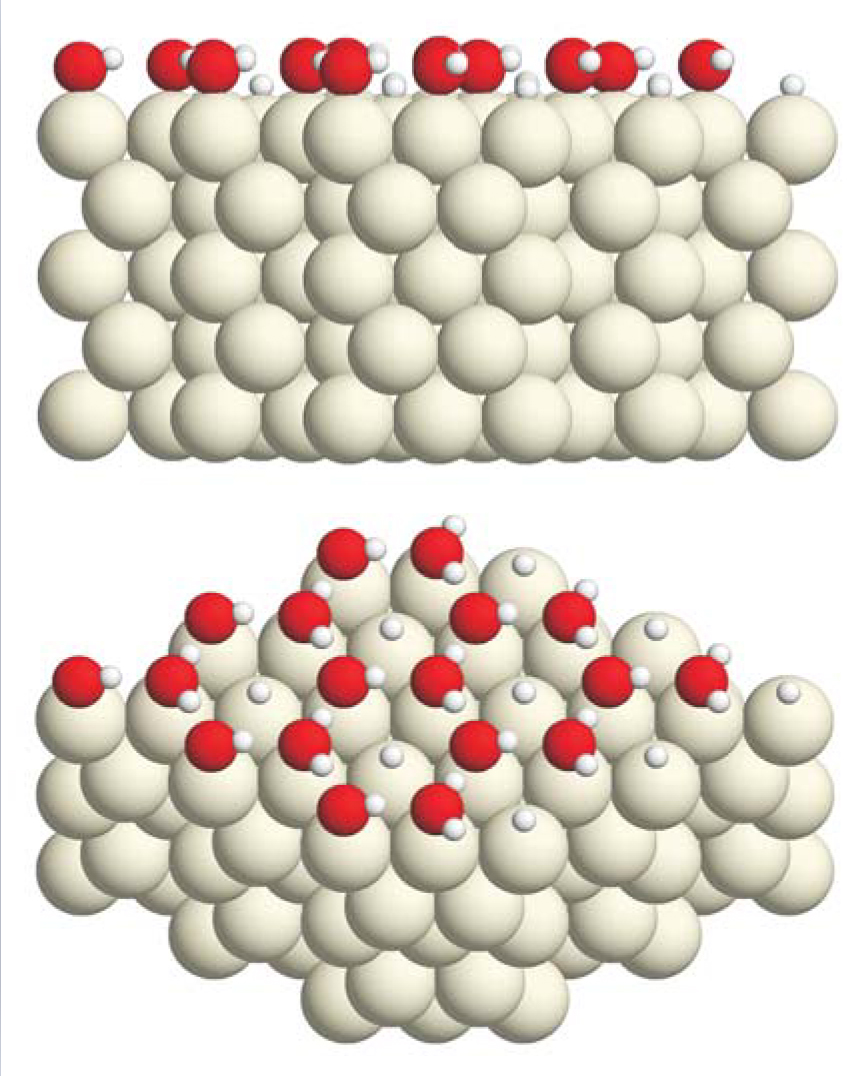
Thermodynamics notwithstanding, the dissociated-structure motif elicited much debate over a question that needs an answer in every high-vacuum, low-temperature experiment: Does an observed structure represent thermal equilibrium or kinetic hindrance? For heavy water on Ru, little doubt was expressed that the dissociated structure represents equilibrium. The worry was that the dissociation observed in the Held-Menzel electron-beam diffraction experiment could be an artifact of electron irradiation. Without irradiation, would dissociation have occurred or would a metastable wetting layer comprising intact water molecules have formed?
Realizing that all H bonds should be parallel to the metal surface in a structure with coplanar O atoms, Andrew Hodgson and coworkers offered a persuasive answer. 9 Using IR absorption spectroscopy to observe H-bond directions, they proved that a metastable, intact H2O layer forms below 150 K on Ru; at warmer temperatures dissociation occurs. The key is that dissociation occurs at a lower temperature than evaporation. If H2O is replaced by D2O, both processes occur near 160 K. And absent a background pressure that compensates evaporation with the deposition of D2O molecules, a thermally dissociated heavy-water layer does not form. The electron beam, accordingly, was responsible for dissociation in the Held-Menzel, heavy-water experiment.
Recent STM images from Miquel Salmeron’s group at Lawrence Berkeley National Laboratory confirm the existence of a low-temperature layer of intact water molecules. Thus, besides spectroscopy, the simulation of low-temperature, atomic-resolution images of adsorbed water is one way to approach the question, How can we make use of our favorite theoretical approaches when the energy differences they yield are indistinguishable from systematic error?
Density functional theory is today’s method of choice for first-principles estimates of the structural energetics of extended condensed-matter systems. Of DFT’s many successes, however, most involve materials governed by strong chemical forces. When one compares candidates for their optimal atomic arrangements, energy differences are correspondingly large, and the unavoidably approximate functional (see
In two recent studies, the problem was bypassed by comparing STM image simulations of DFT optimal structures with actual STM data—instead of relying on calculated energies. The first study 10 was an attempt to understand the appearance of “lace” and “rosette” islands of water on Pd(111). Both structures appear to comprise flat-lying water molecules in their interiors and molecules in another configuration, initially unknown, at their edges. DFT calculations for a rosette island implied only a small preference for edge molecules with O-H bonds dangling downward, toward the metal, versus edge molecules whose dangling H atoms are dissociated and bound to water-free regions of the Pd surface. Image simulation, nevertheless, left little doubt that the first picture is the correct one, as shown in figure 3.

Figure 3. (a) A water “rosette” adsorbed on the close-packed surface of palladium, as seen by scanning tunneling microscopy (STM). (b) An image simulation based on the density-functional-theory optimized model structure (c), in which one of the hydrogen atoms of each water molecule on the rosette periphery lies below its oxygen atom. (d) An image simulation based on the assumption that alternate peripheral water molecules have lost an H atom. Comparison to the STM image makes clear that the “H-down” model is the better representation of experiment. The black parallelogram delimits the unit cell used in the periodic DFT calculation.
(Adapted from ref. 10.)
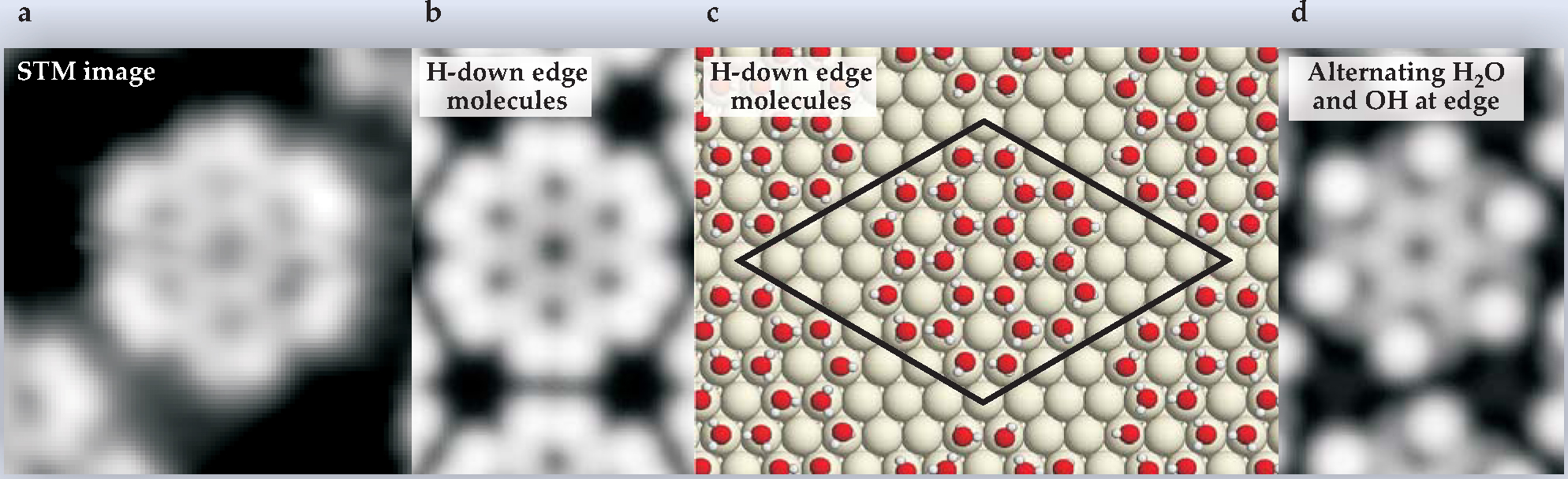
A second example of bypassing energy calculations in favor of STM simulation concerns 1D water islands observed on Cu(110).
7
In the classic bilayer picture, a 1D island cannot be a low-energy structure, because of the cost of the many broken hydrogen bonds at its periphery and because the regular hexagons of the bilayer are a poor match to the long, narrow hexagons of the Cu surface. Javier Carrasco and his colleagues resolved the conflict last year with an unconventional idea—that the molecules of the 1D islands adopt a side-sharing pentagonal arrangement (see Physics Today, May 2009, page 17
Notwithstanding that success, and evoking a continuing issue for theorists, the calculations did not explain on the basis of energies, why 1D islands grow on Cu(110) in preference to 3D ice mounds. Just as for water molecules on low-temperature Pd(111), image simulation based on a DFT-optimized structure was needed to interpret the STM data because systematic error makes today’s DFT energies unreliable in wetting problems.
Water on silver iodide
Worrisome examples are not limited to water on metals. In 1947 Bernard Vonnegut proposed using fine particles of silver iodide to nucleate ice in clouds, a necessary precursor to rainfall. 11 The idea was based on a survey of crystal lattice parameters, which revealed that the lattice constants of hexagonal ice Ih and β-AgI agree to about 1.6% at 0 °C. Admitting an AgI “smoke” to a humid container in the lab was then found to result in rapid formation of ice crystals on the walls. Subsequently, Irving Langmuir of the General Electric Co analyzed experiments conducted in New Mexico to learn if seeding with AgI could make southwest monsoon clouds drop rain. Establishing a causal relationship has not been possible—still, floods and downwind droughts following cloud seeding have been a healthy source of income to legal practitioners ever since.
The scientific question of interest is whether epitaxial match really is the key to ice nucleation efficiency on AgI. Over the decades, most researchers have dismissed that notion, although studies of ice formation in biological systems make the answer less clear. DFT calculations ought to help resolve the matter, but only if the approximate density functional that is used reproduces the epitaxial match found in nature. Otherwise, the functional imposes an unphysical strain on the nucleating ice structure. For water on AgI, I have found mismatches ranging from 4.2% to 7.9%, depending on which of eight semilocal functionals are used. Once again, it appears today’s approximate functionals are not up to the task.
Water multilayers
As noted earlier, knowing the structure of the first layer of water molecules on a surface is not an end in itself but needed for a general understanding of water’s behavior in contact with a material. In many cases, first-principles calculations imply that instead of being ready to donate H atoms to form H bonds with a second layer of water molecules, the first water layer on a hydrophilic surface locates its H atoms either in that layer or between it and the solid. This suggests that the first wetting layer has a propensity to make the surface hydrophobic, a propensity most pronounced at low temperatures.
Two novel techniques have confirmed that theoretical result for water on the close-packed surface of Pt metal. Gregory Kimmel and colleagues approached the problem of multilayer morphology by studying the evaporation of krypton atoms deposited on the water layers. 2 The evaporation onset temperature is higher for Kr atoms that lie closer to the metal, and thus one can determine the surface area covered by a given number of water layers by measuring the number of desorbing Kr atoms in the corresponding thermal peak. In that way, Kimmel’s group showed that although the first water layer on Pt wets the metal completely, additional water grows in 3D mounds, which leave parts of the first layer exposed even at rather high coverages.
Konrad Thürmer and Norman Bartelt drew the same conclusion in 2008 from an STM study. 3 Prior to their work, researchers had not imagined that enough electron current would tunnel through an insulating water layer to make imaging possible. Serendipitously, Thürmer discovered that at high bias (around 6V), ample current tunnels nondestructively from the Pt(111) crystal face through adsorbed water multilayers. This discovery allowed them to observe the dewetting of water layers grown on top of the first to form 3D mounds. That amounted to direct evidence that the final configuration, expressing the hydrophobicity of the first layer, reflects thermodynamics and not kinetic hindrance.
Density functional theory
An elegant and ultimately Nobel Prize-winning theorem proven by Pierre Hohenberg and Walter Kohn in 1964 states that the energy of a condensed system is a functional of its electron density n (r) and that the correct energy density is the one that minimizes the system’s total energy. The theorem means that, in principle, one can find the optimal arrangement of atoms in a solid by iterative solution of a nonlinear differential equation in three Cartesian coordinates—something of a saving compared with a Schrödinger equation with 1023. Nonetheless, the faithfulness of density-functional-theory results to nature depends on how well one approximates the a priori unknown functional. Certain aspects—for example, its asymptotic properties at high electron density and a variety of sum rules it must satisfy—are understood. Still, there is no systematic way to improve a functional, and newer versions are therefore judged purely according to how accurately they predict the structures and formation energies of suites of systems assumed to be representative. Hydrogen-bonded materials ought to present a relatively light challenge to functionals because the hydrogen bond is electrostatic and because we know Coulomb’s law. In practice, the issue is to describe polarization accurately enough in relatively weakly bonded systems. A functional that does this well for water and also accurately describes metals and oxides remains to be developed.
Water multilayers on oxides
To learn why minute particles of kaolinite nucleate ice crystals efficiently and thus seed clouds, a recent theoretical study extended from metals to oxides the notion of a first water layer hydrophobic to the second. 4 A first guess is that a good lattice match between the mineral and ice Ih is the key factor. 11 But the DFT results suggest that structural chemistry is more important.
Kaolinite is a stack of silica-alumina layers, with OH ligands hydrogen-bonding Al atoms of one layer to O atoms that bridge Si atoms of the next. Cleaving kaolinite thus exposes an alumina surface on which the OH ligands are available to form donor H bonds to water molecules and O atoms are also available as H-bond acceptors. That chemical environment and not the good lattice match, argue Xiaoliang Hu and Angelos Michaelides, is the basis of the hydrophilic behavior of kaolinite. 4 According to their calculations, the binding of deposited water is sufficiently strong that a 2D complete-wetting layer is thermodynamically favored. But the strong water-solid bond at zero temperature is achieved only by virtue of a molecular arrangement that leaves no OH bond dangling and thus available to bind a second water-molecule layer (see figure 4). How water multilayers should grow on nominally hydrophilic kaolinite(001) is, accordingly, as unclear as it is on Pt(111). The boundary conditions these surfaces impose on water transport also need new understanding.

Figure 4. Water on a clay. The positions and orientations of a simulated layer of water on a thin slab of the silicate mineral kaolinite (Al2Si2O5(OH)4) were calculated using density functional theory. Oxygen atoms of the water layer are shown in blue, and those that bridge aluminum atoms are green. The remaining O atoms are red. (a) In the side view, no H atoms (small and white) dangle into the vacuum above the water layer. (b) In the top view, water molecules either lie flat, as in the case labeled “F,” or form a donor H bond to the solid, as in the case labeled “D” for “H-down.”
(Adapted from ref. 4.)
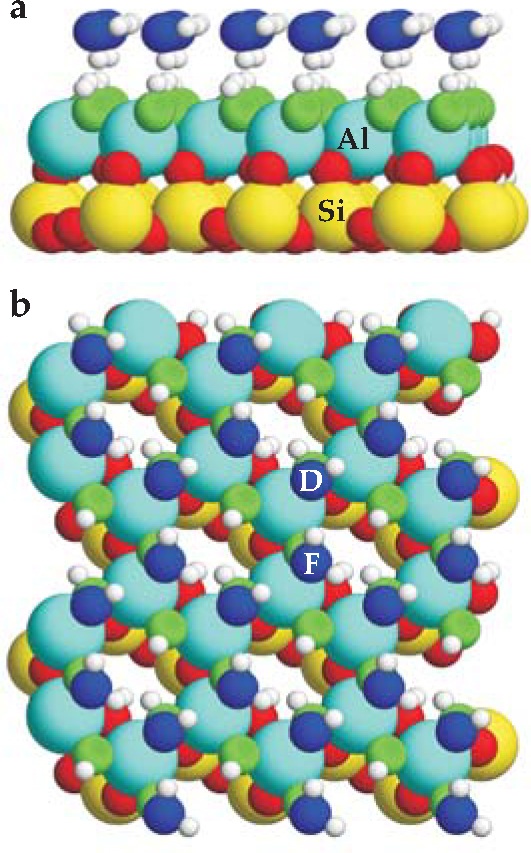
Transport of confined water
That the structure of the first water layer on a material affects transport of adjacent water need not just be a matter of speculation. Direct measurements of resistance to shear should clarify not only how the structure and chemistry of confining surfaces affect the boundary conditions for flow but also the regime wherein continuum hydrodynamics—and specifically the concept of viscosity—is meaningful. They should tell the degree and nature of solute effects and whether incipient crystallization—the layering of water molecules—gives rise to oscillatory variations of friction with channel thickness. One day we will know the answers; for now, results conflict, sometimes spectacularly.
The conflicts might involve inadequate surface characterization, but not a lack of appropriate instrumentation. For example, the interfacial force microscope (IFM), a cousin to the atomic force microscope (AFM), is designed to study adhesive and frictional forces in liquid or air between a probe tip and a flat sample. 12 The tip-sample forces are measured not by the bending of a cantilever spring but by observing how much charge must be delivered to appropriately positioned capacitors to counteract the force (see figure 5). The design is advantageous in that the tip-sample spacing and approach speed are under the experimenter’s control, even when strong adhesive forces would otherwise overcome the resistance to the bending of a soft spring or mica sheet and end the experiment with an abrupt “snap to contact.”

Figure 5. The interfacial force microscope, shown schematically at left. The force between tip and sample is counterbalanced by delivery of charge to the capacitors, allowing a force measurement with no mechanical deflection. At right, data from an IFM experiment by Ryan Major and colleagues show the forces experienced by an OH-functionalized tungsten tip that approaches an OH-covered silica surface in water at different speeds. (Each plotted point is scaled by a factor of 30 Å/s divided by the tip speed.) Between 10 and 30 Å, the resistance of the water to being squeezed out of the tip-sample gap scales with speed, suggesting a viscous response. The gray curve is a prediction based on hydrodynamics at low Reynolds number.
(Figure courtesy of Jack Houston.)
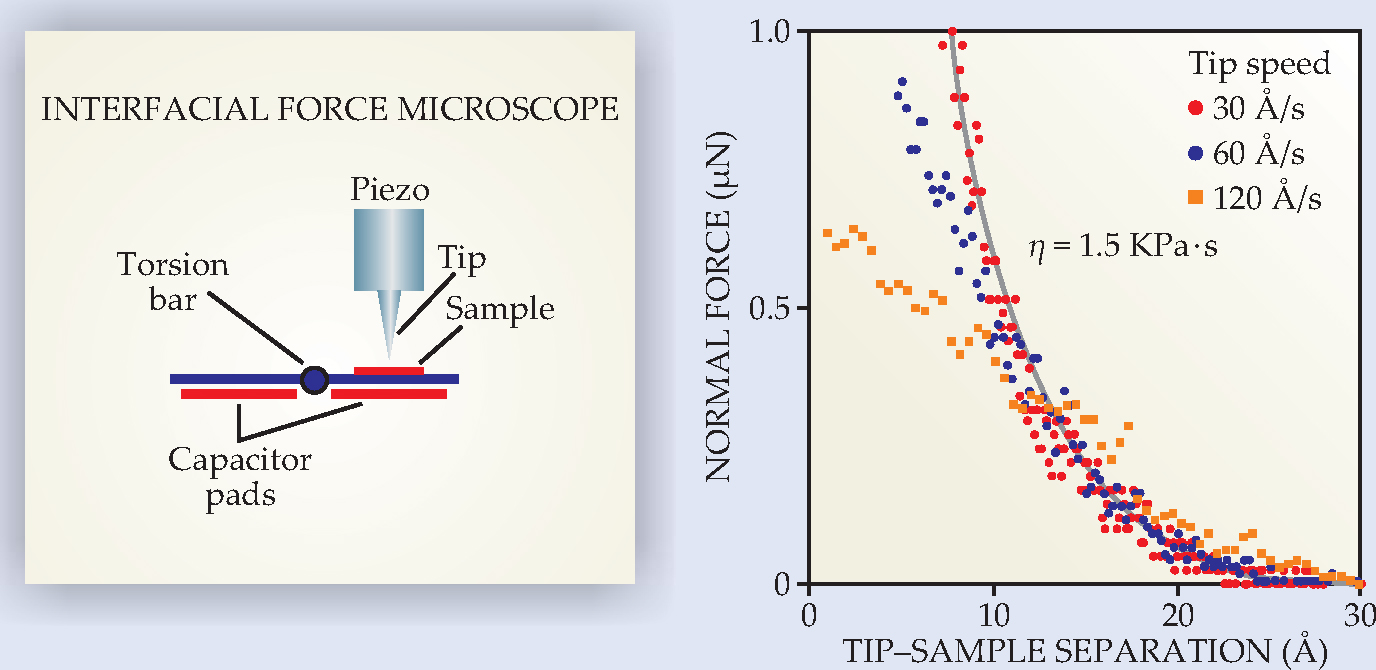
The remarkable result of IFM studies of water confined to 1-2 nm between a tip and sample is that the measured force as a function of relative tip-sample speed implies a water viscosity roughly a million times that of water in bulk. 13 This result, obtained for a variety of hydrophilic tip and sample combinations and with the tip approaching the sample or oscillating parallel to it, is orders of magnitude larger than what has been found when water is confined between the hydrophilic mica sheets of a surface force balance. 14 (The SFB’s design is discussed below.)
Locking water molecules into layers, as in a crystal, is a conceivable source of greatly enhanced shear resistance near a surface. But x-ray reflection measurements of water on hydrophilic oxide surfaces typically reveal only one or two well-defined water-molecule layers, largely within 0.5 nm of the interface. 15 Beyond that distance, layering should not affect forces much. And, indeed, neither the IFM nor the SFB shows evidence for oscillatory forces at tip-sample separations over a nanometer. That said, AFM measurements for water between a silica tip and a mica sample do show oscillations and a substantial enhancement to the viscosity at separations smaller than 2 nm. 16
Water on mica
Water on mica has been the subject of many transport studies that use either Jacob Israelachvili’s surface force apparatus (SFA) or Jacob Klein’s SFB. 17 The liquid is confined between two cylindrical mica sheets, with the cylinders at right angles. The distance between the sheets is measured interferometrically (in the SFA) or capacitively (in the SFB), and the force opposing their approach toward each other, or the sliding of one sheet relative to the other, by an arrangement of springs. Contrary to findings with the IFM, SFB results imply that confined water is not much more viscous than water in bulk. Neither technique, however, shows evidence for layering, even down to a fraction of a nanometer.
To understand how proximity to the mica surface affects the arrangement of water molecules, Salmeron and coworkers developed and applied a novel scanning probe technique; this (decade old) work is reviewed in . Ordinary STM was not an option because muscovite mica is a very good insulator, and ordinary AFM would disturb the water layer too easily. To surmount these obstacles, they used the rather low resolution technique they dubbed scanning polarization force microscopy, in which an AFM tip retracted to a distance of a few hundred angstroms detects the presence of water by the degree to which an electric field affects the force the tip experiences. Using this tool, the LBNL group found that at 20-40% relative humidity and room temperature, water adsorbs as 2D crystals; that is, the water islands observed are faceted along the principal lattice directions of the underlying mica.
With the sense that crystallinity expresses underlying simplicity, several computational groups have hoped to account for the 2D crystal structure at the molecular level by using empirical force fields or DFT. But their efforts have been frustrated by several complexities. One is that surface potassium atoms, which bind mica’s silica-alumina-silica layers to each other, are water soluble. Another is that the mica surface’s Al atoms are, within certain rules, randomly located. Also, x-ray reflectivity measurements require that a model wetting layer have a certain fraction of water molecules lying low in the array of depressions intrinsic to the mica surface.
On the basis of a molecular dynamics simulation, Artur Meleshyn of the University of Hannover in Germany has proposed that the low-lying water molecules in surface holes are responsible for the observation of island facets aligned to the substrate and that K atoms rising out of their surface hollows to become fully solvated are what drive wetting energetically. One might hope this picture would stand the test of time. My own DFT optimization of a snapshot from the simulation, however, suggests that 3D mounds of water on mica are significantly better bound.
Does that result prove that the model wetting layer is missing a physically or chemically important feature? Given the level of systematic error in today’s density functionals, one is hard put to say. Accordingly, water transport on mica is not yet a timely theory problem at the molecular scale.
Where we stand
Access to large, powerful computers and modern algorithms raises the appealing prospect that simulations will reveal how the first water layer guides epitaxy and governs transport and chemistry at water-solid interfaces. To achieve that level of understanding, theorists require a density functional that accounts reliably for the energy differences among hydrogen-bonded structures. Accuracy of DFT binding energies to 10 meV or better, per H bond, is needed. Until such is available, progress in deriving insight from data will remain fitful. Most needed from experiment is quantitative, atomic-scale information. Scanning probe images have been helpful in devising model wetting structures. Atomic coordinates from diffraction data, for example, would be better. They would constrain and thus help to improve the reliability of theoretical models.
Still, 21st-century research into the nature of the first wetting layer on a solid has borne important fruit. On the evidence, we have learned that adsorbed water can organize nonhexagonally. We have discarded the ideas that H bonds around a surface O atom must be arranged tetrahedrally and that water molecules must adsorb intact on precious metals. As a result, we have had to refine our considerations of what might be the molecular basis of the “no-slip” boundary condition for water transport and of how an ice crystal nucleates. The recent confrontation of theory and experiment has led to an understanding of wetting structures that is far richer than the imagined ideal, icelike bilayers—no longer a paradigm, at best a straw man.
My many discussions with Norman C. Bartelt are gratefully acknowledged. This work was supported by the US Department of Energy’s Office of Basic Energy Sciences, division of materials sciences and engineering, and Sandia National Laboratories.
References
1. P. G. de Gennes, Rev. Mod. Phys. 57, 827 (1985). https://doi.org/10.1103/RevModPhys.57.827
2. G. A. Kimmel et al., Phys. Rev. Lett. 95, 166102 (2005). https://doi.org/10.1103/PhysRevLett.95.166102
3. K. Thürmer N. C. Bartelt, Phys. Rev. Lett. 100, 186101 (2008). https://doi.org/10.1103/PhysRevLett.100.186101
4. X. L. Hu A. Michaelides, Surf. Sci. 601, 5378 (2007). https://doi.org/10.1016/j.susc.2007.09.012
5. P. A. Thiel T. E. Madey, Surf. Sci. Rep. 7, 211 (1987). https://doi.org/10.1016/0167-5729(87)90001-X
6. M. A. Henderson, Surf. Sci. Rep. 46, 1 (2002). https://doi.org/10.1016/S0167-5729(01)00020-6
7. J. Carrasco et al., Nat. Mater. 8, 427 (2009). https://doi.org/10.1038/nm0502-427
8. P. J. Feibelman, Science 295, 99 (2002). https://doi.org/10.1126/science.1065483
9. C. Clay, S. Haq, A. Hodgson, Chem. Phys. Lett. 388, 89 (2004). https://doi.org/10.1016/j.cplett.2004.02.076
For a recent review, see A. Hodgson S. Haq, Surf. Sci. Rep. 64, 381 (2009). https://doi.org/10.1016/j.surfrep.2009.07.00110. J. Cerdá et al., Phys. Rev. Lett. 93, 116101 (2004). https://doi.org/10.1103/PhysRevLett.93.116101
11. B. Vonnegut, J. Appl. Phys. 18, 593 (1947).
12. S. A. Joyce J. E. Houston, Rev. Sci. Instrum. 62, 710 (1991). https://doi.org/10.1063/1.1142072
13. M. P. Goertz, J. E. Houston, X.-Y. Zhu, Langmuir 23, 5491 (2007). https://doi.org/10.1021/la062299q
14. U. Raviv et al., Langmuir 20, 5322 (2004). https://doi.org/10.1021/la030419d
15. P. Fenter N. C. Sturchio, Prog. Surf. Sci. 77, 171 (2004). https://doi.org/10.1016/j.progsurf.2004.12.001
16. T.-D. Li et al., Phys. Rev. B 75, 115415 (2007). https://doi.org/10.1103/PhysRevB.75.115415
17. E. Kumacheva, Prog. Surf. Sci. 58, 75 (1998). https://doi.org/10.1016/S0079-6816(98)00017-3
18. P. J. Feibelman, Langmuir 20, 1239 (2004). https://doi.org/10.1021/la035430s
More about the Authors
Peter Feibelman is a senior scientist at Sandia National Laboratories in Albuquerque, New Mexico.
Peter J. Feibelman. Sandia National Laboratories, Albuquerque, New Mexico, US .




