Features

Article

The Bethe ansatz after 75 years

JAN 01, 2007

A 1931 result that lay in obscurity for decades, Bethe’s solution to a quantum mechanical model now finds its way into everything from superconductors to string theory.

DOI: 10.1063/1.2709557

Murray T. Batchelor

Hans Bethe introduced his now-famous ansatz to obtain the energy eigenstates of the one-dimensional version of Werner Heisenberg’s model of interacting, localized spins in a solid. ^1,2 Although it is among Bethe’s most cited works and has a wide range of applications, it is rarely included in the graduate physics curriculum except at the advanced level. The 75th anniversary of the Bethe ansatz is appropriately marked by reflecting on the impact of Bethe’s result on modern physics, ranging from its profound influence on the field of exactly solved models in statistical mechanics to insights into the subtle nature of quantum many-body effects observed in cold quantum gases.

Bethe (figure 1) completed his PhD in theoretical physics under Arnold Sommerfeld in 1928. During his subsequent time at the University of Munich, Bethe used a traveling fellowship to go to Cambridge in the fall of 1930 and to Rome during the spring terms of 1931 and 1932. His 1931 paper, published in German in Zeitschrift für Physik, was submitted from Rome. That period was one of the most exciting times in the history of physics; the theory of quantum mechanics was being refined and applied to reveal the intricate nature of the quantum realm. Those breathtaking developments, along with encounters with pioneers such as Heisenberg, Paul Dirac, and Enrico Fermi, clearly had a strong influence on Bethe’s research. (For further biographical details, see the October 2005 Hans Bethe special issue of Physics Today; for Bethe’s own account of his time spent with Fermi in Rome see Physics Today, June 2002, page 28 .)

PTO.v60.i1.36_1.f1.jpg — **Figure 1. Hans Bethe** early in his career.

AIP EMILIO SEGRÈ VISUAL ARCHIVES
View larger

**Figure 1. Hans Bethe** early in his career.
AIP EMILIO SEGRÈ VISUAL ARCHIVES

Download

Solving the Heisenberg model

In German “der Ansatz” can mean “basic approach,” “rudiment,” or “beginning.” A mathematical ansatz is a sort of hypothesis: an attempt at a solution followed by a demonstration that it is correct, rather than a solution derived using a previously known method.

The Bethe ansatz began as a solution to the Heisenberg model, a 1D array of quantum mechanical spin- $\frac{1}{2}$ particles at fixed locations. Pairs of nearest-neighbor spins interact, and periodic boundary conditions mean that the last spin interacts with the first. Solving the model means finding all of the eigenstates of the Hamiltonian and their corresponding energies.

Spins in the Heisenberg model can point in any direction, but any state of the system can be written as a linear combination of basis states in which each of the spins is either spin up or spin down in a specified direction. Angular momentum in the direction of quantization is conserved, which means that each eigenstate is a linear combination of basis states that all have the same number of down spins. In other words, the Hamiltonian for an array of L spins is a block-diagonal matrix, with one block for each number of down spins. It is useful to think of each down spin as a quasiparticle, and the state of all up spins as the vacuum state.

The wavefunction for a single quasiparticle looks very much like the wavefunction for a free particle in a ring: a plane wave of the form exp(ikx), with an energy that depends on the wavenumber k, which itself must be an integer multiple of 2π/L. Eigenstates with two or more particles are more complicated because the particles interact—but the interaction is short-range, since only pairs of nearest-neighbor spins contribute to the Hamiltonian.

Bethe developed his ansatz by looking at those regions, in the configuration space of quasiparticles, where all the quasiparticles are separated from one another. For n quasiparticles, there are n! such regions in the n-dimensional configuration space, one for each ordering of the quasiparticles. Bethe’s big idea was to hope that the wavefunction in each region is a superposition of plane waves, as if the quasiparticles were not interacting at all. By matching the wavefunctions on the interfaces between those regions, he worked out a system of equations, shown in box 1, for the coefficients and wavenumbers of the plane waves. The wavenumbers were then no longer integer multiples of 2π/L. Taking the place of that constraint is a complicated set of equations known as the Bethe-ansatz equations, or simply the Bethe equations.

Bethe went on to show that his ansatz gives 2^L energy eigenvalues, where L is the length of the chain. Since 2^L is the total number of eigenstates, he had found the complete energy eigenspectrum for any finite system.

Bethe never returned to the problem. It was next picked up in 1938 by Lamek Hulthén, working in Leiden, in the Netherlands. Hulthén’s work pertained to the antiferromagnetic case of the Heisenberg model, in which antiparallel spins are energetically preferred. Hulthén used Bethe’s solution to the finite system to obtain the ground-state energy per site in the limit of an infinitely long chain. ³ Hulthén correctly guessed that the wavenumbers describing the ground state form a uniform distribution in the infinite size limit. Because of Hulthén’s contribution, the Bethe ansatz is sometimes called the Bethe–Hulthén hypothesis.

Interacting bosons and fermions

Hulthén’s work was followed by a long hiatus for the Bethe ansatz. Its next appearance was not until 1963, but the development was a remarkable one: the exact solution of a 1D model of interacting spinless bosons. ⁴ In that model, now known as the Lieb–Liniger Bose gas after Elliott Lieb and Werner Liniger, N bosons interact on a line of length L via zero-range contact potentials, as described in box 2. Unlike the 1D Heisenberg model, in which spins are fixed at discrete lattice sites, the Lieb–Liniger Bose gas is a continuum model in which the particles (equal spinless mass bosons) are free to move along a line. The form of the wavefunction is precisely that of the Bethe ansatz, but with a different form of the two-body interaction term, and therefore a different energy eigenspectrum. Again, the Bethe ansatz provides the complete solution to the model. An important feature of the model is that the interaction strength, parameterizing the relative magnitudes of the kinetic and potential energy terms, is variable. In the limit of infinite interaction strength, the model reduces to the model of “impenetrable” hard-core bosons discussed by Marvin Girardeau in 1960. ⁵ That limit is special because no two impenetrable bosons can occupy the same state, which means that the strongly interacting bosons effectively behave like noninteracting fermions.

The problem of N fermions interacting in one dimension can be solved using the same method, but now one has to do additional work to account for the spin degrees of freedom. ^6,7 The result is an even more complicated, nested set of Bethe-ansatz equations. The energy eigenspectrum is still given in terms of the wavenumbers, but the spin degrees of freedom influence the values of those wavenumbers. Of particular interest in the 1D fermion model are the bound states for attractive interaction and the differing behaviors of the bound fermion pairs for different values of the interaction strength. For strong attraction, the bound states behave like tightly bound molecular dimers (a condensation-like behavior), but in the weakly attractive regime, the system describes loosely bound Cooper pairs (a superconductivity-like behavior).

The more complicated Bethe-ansatz equations of the interacting-fermion type appear in a number of other models, including the 1D Hubbard model solved by Lieb and Fred Wu, which describes electron correlations in a narrow energy band. ⁸ Those fundamental models of interacting particles, solved in the 1960s in terms of the Bethe ansatz, are enjoying a revival of interest due to the striking experimental advances in quantum atom optics.

The ice model

Applications of the Bethe ansatz extend to systems seemingly unrelated to the 1D problem in quantum mechanics that Bethe originally considered. The Bethe-ansatz solution to the Heisenberg model involves the diagonalization of the Hamiltonian, a 2^L by 2^L block-diagonal matrix. If a similar matrix appears in a model of another type, then that model may also admit a Bethe-ansatz solution.

Such is the case of the ice model, a 2D model in statistical mechanics, so called because of its resemblance to the crystalline structure of ice. An oxygen atom sits at each vertex of a square lattice with periodic boundary conditions, and a hydrogen atom sits on each edge. Each hydrogen atom is closer to one of the neighboring oxygen atoms than to the other. The “ice rule” requires that each lattice site contain a molecule of H₂O—that is, that each oxygen has two near neighboring hydrogens and two far neighboring hydrogens. The model is usually represented graphically by placing an arrow on each edge of the lattice to represent the position of the hydrogen. The ice model is also called the six-vertex model, because each vertex has six allowed configurations of two inward-pointing and two outward-pointing arrows.

Solving the model means calculating the partition function, a count of all allowed configurations weighted according to their energies. In actual ice, all allowed configurations have the same energy, but the model is generalized by assigning different energies to the six different vertex configurations. In 1967 Lieb solved the ice model by calculating the partition function in terms of the eigenvalues of a matrix called the transfer matrix. ⁹

If two adjacent rows of vertical arrows are specified, there are at most two ways of filling in the horizontal arrows between them; if the rows of vertical arrows are not identical, then there is at most one way. The energy of a configuration is therefore almost completely determined by the configuration of the vertical arrows. For a lattice of width N, a 2^N by 2^N transfer matrix has elements describing the contributions that are made to the partition function by all the possible pairs of adjacent rows of vertical arrows.

In any configuration of the ice model, two adjacent rows (in fact, any two rows) of vertical arrows must contain the same number of down arrows. The transfer matrix is therefore a block-diagonal matrix, with one block for each number of down arrows from 1 to N. The “conserved” down arrows in the ice model play the same role as the conserved quasiparticles in the Heisenberg model.

Lieb showed that the eigenvectors of the transfer matrix can be obtained in terms of the Bethe ansatz. The solution of the ice problem created great excitement at the time and was on a par with Lars Onsager’s solution of the 2D Ising model. The six-vertex ice model was soon refined and generalized, and the study of exactly solved lattice models got under way in earnest.

The similarity between the Bethe-ansatz solution of the six-vertex model and the generalization of Bethe’s solution to a variant of the Heisenberg spin chain was soon noticed. Not only are the two models both solvable using the Bethe ansatz, but their respective matrices share the same eigenvectors. In other words, the Heisenberg model Hamiltonian commutes with the ice model transfer matrix. ¹⁰ The connection between those two models is a manifestation of a more general connection between 1D quantum problems and 2D classical statistical-mechanics problems. All this pointed to the power of the Bethe-ansatz approach and set the stage for the remarkable developments to follow.

Technicalities of the Bethe ansatz

The Hamiltonian for a Heisenberg spin chain of length L is

$H = \frac{J}{2} \sum_{i = 1}^{L} (σ_{i} \cdot σ_{i + 1} + 1),$

where σ_{i =} (σ_x, σ_y, σ_z )_i are the Pauli spin matrices at site i. The constant J is negative in the case of the Heisenberg ferromagnet (in which parallel spins are energetically preferred) and positive for the Heisenberg antiferromagnet (where antiparallel spins are preferred). Periodic boundary conditions are imposed so that σ _L+1 = σ ₁. The eigenstates are linear combinations of basis states

$| ψ 〉 = \underset{1 \leq X_{1} < … < X_{n} \leq L}{Σ} a (X_{1}, …, X_{n}) | X_{1}, …, X_{n} 〉,$

where |x ₁, …, x_n 〉 is the state in which the n spins x ₁, …, x_n are overturned. Bethe’s great insight was to deduce that the amplitudes a(x ₁, …, x_n ) are of the form

$a (x_{1}, …, x_{n}) = \underset{P \in S_{n}}{Σ} A_{P} exp (Σ_{j = 1}^{n} i k_{p_{i}} x_{i}),$

where the sum over P ε S_n is over all n! permutations P = {p ₁, …, p_n } in S_n , the group of permutations of the integers 1, …, n. Bethe was able to use that ansatz to obtain the coefficients A_P in terms of the two-body interaction terms s_jℓ = 1 −2exp(ik_ℓ ) + exp(ik_j + ik_ℓ ). Specifically, he found

$A_{P} = ɛ_{P} \underset{1 \leq i < j \leq n}{Π} S_{P_{j} P_{i}},$

where ε_P is the signature of the permutation. The variables kj must satisfy the system of equations

$exp (i k_{j} L) = {(- 1)}^{n - 1} \underset{ℓ \neq j}{Π} \frac{S_{ℓ j}}{S_{j ℓ}}$

for j = 1, …, n. The above equations for the wavenumbers k_j are known as the Bethe-ansatz equations. Solutions for k_j give the energy eigenvalues in the form

$E = J L + J Σ_{i = 1}^{n} (2 cos k_{j} - 2) .$

Integrability and the Yang–Baxter equation

Bethe found that his many-particle problem reduced to dealing with the way in which two particles come together. His ansatz thus effectively factorizes interactions among many particles into two-body interactions. Such factorization is intimately entwined with the concept of integrability. By way of analogy, in classical mechanics a system is integrable if all the constants of motion can be calculated. For example, the two-body gravitational problem is integrable, but the three-body problem is not. The long-range nature of the gravitational force means that the three-body interaction cannot be reduced to a series of two-body interactions. Almost without exception, a given model system is integrable if it can be solved in terms of the Bethe ansatz.

A key step in C. N. Yang’s solution of the 1D interacting fermion problem was the introduction of operators that obey what is now called the Yang–Baxter equation. The same concept appeared in a different guise in Rodney Baxter’s solution of the eight-vertex model (similar to the ice model, but with two additional vertex configurations allowed) as the condition for commuting transfer matrices. ^10,11 For example, in the context of the Heisenberg spin chain or the Lieb–Liniger Bose gas, the three-body Bethe ansatz wavefunction amplitudes A_abc can be written in the general form A_abc = Y_abA_bac and A_abc = Y_bcA_acb’ , where Y_ab = −S_ba/S_ab. In terms of those operators, two possible ways exist to get from A_abc to A_cba , namely

$A_{c b a} = ϒ_{a b} ϒ_{a c} ϒ_{b c} A_{a b c} and A_{c b a} = ϒ_{b c} ϒ_{a c} ϒ_{a b} A_{a b c} .$

Both paths must be equivalent, with

$ϒ_{a b} ϒ_{b a} = 1 and ϒ_{a b} ϒ_{a c} ϒ_{b c} = ϒ_{b c} ϒ_{a c} ϒ_{a b} .$

The relations have a simple graphical interpretation. The first is a unitarity-type relation, and the second is a form of the Yang–Baxter equation as shown in figure 2, also called the star-triangle relation.

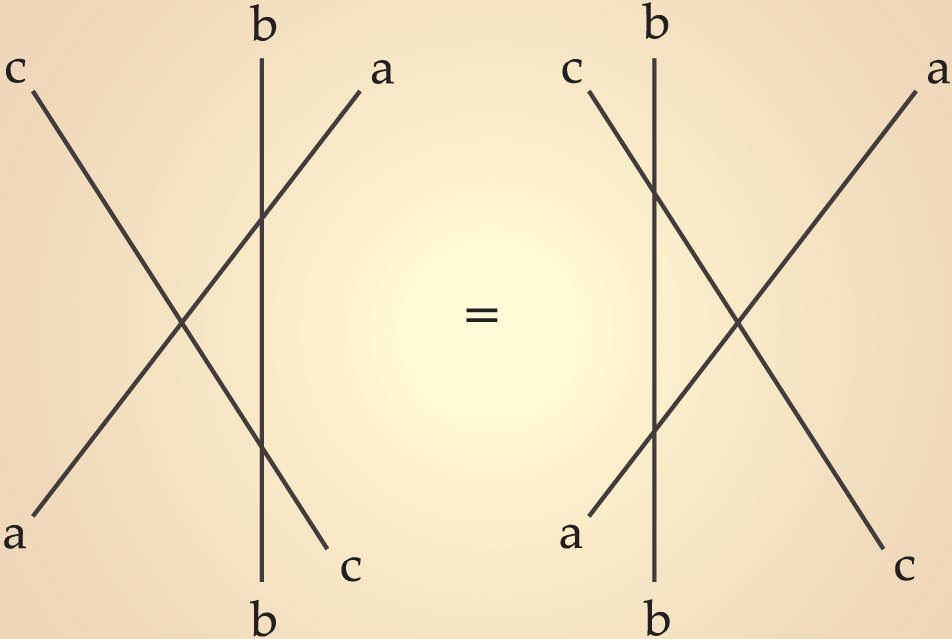
PTO.v60.i1.36_1.f2.jpg — **Figure 2. Graphical interpretation** of the Yang–Baxter equation *Y_abY_acY_bc = Y_bcY_acY_ab* . It can be viewed as a space-time plot of the scattering of three particles *a, b*, and c, with time going from bottom to top. The scattering is seen to factor into successive two-body interactions.
View larger

**Figure 2. Graphical interpretation** of the Yang–Baxter equation *Y_abY_acY_bc = Y_bcY_acY_ab* . It can be viewed as a space-time plot of the scattering of three particles *a, b*, and c, with time going from bottom to top. The scattering is seen to factor into successive two-body interactions.

Download

The Yang–Baxter equation provides a set of relations that can be solved to yield new integrable models. That realization sparked a revolution in the fields of exactly solved models in statistical mechanics and integrable models in quantum field theory. In quantum field theory, the Yang–Baxter equation describes the scattering of particles in one spatial dimension plus time (“(1 + 1) dimensions”), a class of problems that caught Richard Feynman’s interest shortly before he died. In one of his last articles, he wrote: ¹²

I got really fascinated by these (1 + 1)-dimensional models that are solved by the Bethe ansatz and how mysteriously they jump out at you and work and you don’t know why. I am trying to understand all this better.

The theory of integrability also has an influence on developments in mathematics. Investigation into the mathematical structure of the Yang–Baxter equation led to the introduction of the theory of quantum groups and to significant advances in the theory of links, braids, and knot invariants. More recently, the Bethe ansatz itself has led to some intriguing developments in the field of combinatorics. Specifically, components of the ground-state wavefunction for a variant of the Heisenberg spin chain can be used to count combinatorial objects called alternating sign matrices. ¹³ Recent developments in string theory involve a surprising connection between semi-classical strings in super Yang–Mills theory and the Bethe-ansatz solution of the 1D Heisenberg spin chain. ¹⁴

The interacting boson model

The Lieb–Liniger Bose gas, in which N bosons interact on a line of length L via zero-range δ-function contact potentials, is defined in terms of the Hamiltonian

$H = - Σ_{i = 1}^{N} \frac{\partial^{2}}{\partial x_{i}^{2}} + 2 c \underset{1 \leq i < j \leq N}{Σ} δ (x_{i} - x_{j}) .$

The particles are located at the positions x ₁ < x ₂ < …< x_N , a set of positions known as the fundamental domain. A key feature of the model is the variable interaction strength c. The form of the wavefunction is precisely that of the Bethe ansatz, described in box 1, with the two-body interaction terms given by s_ab = k_a − k_b + ic. The Bethe-ansatz equations are

$exp (i k_{j} L) = - Π_{ℓ = 1}^{N} \frac{k_{j} - k_{ℓ} + i c}{k_{j} - k_{ℓ} - i c}$

for j = 1, …, N. Solutions of the equations give the energy eigenvalues

$E = Σ_{j = 1}^{N} k_{j}^{2} .$

Out of the paper, into the lab

Systems solved by the Bethe ansatz occasionally appear in condensed-matter physics experiments. For example, a number of compounds are made up of effectively 1D arrays of spins, which behave like the 1D Heisenberg spin chain. Notable models that are relevant to experiments in condensed-matter physics and whose solutions involve the Bethe ansatz include the Gaudin long-range magnets, the Bardeen-Cooper-Schrieffer electron pairing model, the Kondo model, and the Anderson model.

Experiments designed to realize the more fundamental models solved in terms of the Bethe ansatz also have value. The spectacular recent progress in trapping atoms in optical lattices ¹⁵ may provide the most fertile testing ground for the realization of 1D quantum mechanical models. Indeed, from those studies, the exactly solved interacting Bose gas has emerged as a fundamental model of quantum many-body physics of direct experimental relevance.

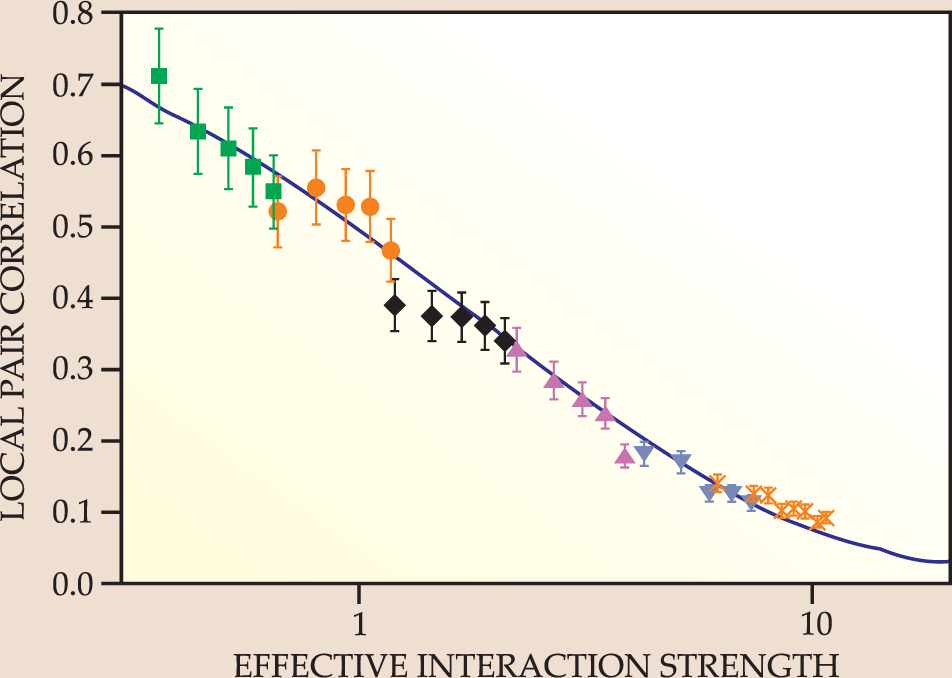
One particularly striking example involves the experimental realization of the 1D Lieb–Liniger Bose gas over a wide range of interaction strengths. In experiments performed by Toshiya Kinoshita, Trevor Wenger, and David Weiss, freely moving 1D Bose gases of cold rubidium-87 atoms are confined in an ensemble of long cigar-shaped tubes made by a combination of two light traps. ^16,17 The atomic interaction strength can be varied by changing the trap depths. The measurements of the total 1D energy fit the Lieb–Liniger exact solution for the ground state of the interacting 1D Bose gas. ¹⁶ Moreover, the researchers obtained the local pair-correlation function by measuring photoassociation rates over a range of interaction strengths, as shown in figure 3. ¹⁷ The local pair-correlation function is proportional to the probability of observing two particles in the same place, so it should decrease as the interaction strength increases, and tend to zero in the strong-interaction limit in which the bosons behave like noninteracting fermions. The experimental data are in excellent agreement with the theoretical result obtained using the Bethe ansatz. The experiments give a direct observation of the fermionization of bosons.

PTO.v60.i1.36_1.f3.jpg — **Figure 3. Comparison between experiment** and theory for the local pair-correlation function versus effective interaction strength of the one-dimensional Bose gas. For strong coupling the local pair-correlation function approaches zero, indicating that strongly interacting bosons act like noninteracting fermions. The solid line is obtained from the Lieb–Liniger result, which uses the Bethe ansatz.

(Adapted from ref. 17.)
View larger

**Figure 3. Comparison between experiment** and theory for the local pair-correlation function versus effective interaction strength of the one-dimensional Bose gas. For strong coupling the local pair-correlation function approaches zero, indicating that strongly interacting bosons act like noninteracting fermions. The solid line is obtained from the Lieb–Liniger result, which uses the Bethe ansatz.
(Adapted from ref. 17.)

Download

Given the ongoing experimental advances in the trapping of fermions in low dimensions, the 1D interacting fermion model may soon be experimentally realized. Then the door should open for many other exactly solved models that have essentially lain fallow over the years: the multi-component Fermi model, a mixed equal-mass boson–fermion model, a model of a spinor Bose gas, and a model of interacting anyons, among others.

Optical-lattice experiments may even allow the realization of the Heisenberg model and other integrable quantum spin systems. By developing cold gases of polar molecules as a quantum simulator for strongly correlated condensed-matter systems, researchers may be able to construct a complete toolbox to realize effective spin models with desired forms of two-spin interactions and coupling strengths. ¹⁸ That tantalizing development parallels the growing interest in integrable quantum many-body systems and their applications to quantum entanglement, quantum information theory, and quantum computation, all of which depend on the quantum interference of amplitudes of mutually exclusive events. Of course, quantum interference is not present in any classical dynamics, information, or probability theory. However, it is a vital ingredient in quantum systems integrable by the Bethe ansatz.

After 75 years the Bethe ansatz is alive and well. It has been used to solve genuine interacting quantum many-body systems for which perturbative approaches and mean-field theories often fail. In the case of interacting bosons and fermions, the spatial confinement to one dimension leads to enhanced dynamics and correlations, and ultimately to new quantum phases. Because of its underlying mathematical structure and the richness of its results, the Bethe ansatz has had a remarkable impact on several fields, with many surprises along the way. Given the recent advances in the manipulation of atoms in optical lattices, no doubt many more surprises lie ahead.

References

1. H. A. Bethe, Z. Phys. 71, 205 (1931).
2. M. T. Batchelor, in Encyclopedia of Mathematical Physics, Elsevier,Boston (2006), p. 253. https://doi.org/10.1016/B0-12-512666-2/00172-3
3. L. Hulthén, Ark. Mat. Astron. Fys. A 26, 1 (1938).
4. E. H. Lieb, W. Liniger, Phys. Rev. 130, 1605 (1963)
E. H. Lieb Phys. Rev. 130, 1616 (1963).
5. M. Girardeau, J. Math. Phys. 1, 516 (1960).
6. J. B. McGuire, J. Math. Phys. 5, 622 (1964).
7. M. Flicker, E. H. Lieb, Phys. Rev. 161, 179 (1967)
M. Gaudin, Phys. Lett. A 24, 55 (1967)
C. N. Yang, Phys. Rev. Lett. 19, 1312 (1967)
B. Sutherland, Phys. Rev. Lett. 20, 98 (1968).
8. E. H. Lieb, F. Y. Wu, Phys. Rev. Lett. 20, 1445 (1968).
9. E. H. Lieb, Phys. Rev. 162, 162 (1967).
10. R. J. Baxter, Exactly Solved Models in Statistical Mechanics, Academic Press, New York (1982).
11. R. J. Baxter, Ann. Phys. (N.Y.) 70, 193 (1972).
12. R. P. Feynman, Asia-Pacific Physics News 3, 22 (June/July 1988).
13. A. V. Razumov, Y. G. Stroganov, J. Phys. A 34, 3185 (2001)
M. T. Batchelor, J. de Gier, B. Nienhuis, J. Phys. A 34, L265 (2001).
14. J. A. Minahan, K. Zarembo, J. High Energy Phys. 03, 013 (2003)
N. Beisert, M. Staudacher, Nucl. Phys. B 670, 439 (2003)
J. A. Minahan, J. Phys. A 39, 12657 (2006).
15. I. Bloch, Nat. Phys. 1, 23 (2005).
16. T. Kinoshita, T. Wenger, D. S. Weiss, Science 305, 1125 (2004).
17. T. Kinoshita, T. Wenger, D. S. Weiss, Phys. Rev. Lett. 95, 190406 (2005).
18. A. Micheli, G. K. Brennen, P. Zoller, Nat. Phys. 2, 341 (2006).

More about the Authors

Murray Batchelor is head of the department of theoretical physics and a member of the Mathematical Sciences Institute at the Australian National University in Canberra.

Murray T. Batchelor. Mathematical Sciences Institute, Australian National University, Canberra.