Intuitive or rational? Students and experts need to be both

Suppose you are teaching an introductory-physics course. You ask your students to consider a box on a rough, level surface that remains at rest while a horizontal 30 N force is applied to it (see figure 1a). Your students seem to recognize that because the box is at rest, the frictional force must be equal in magnitude to the applied force. Using that realization, they correctly deduce that neither the mass of the box nor the coefficient of static friction is relevant for determining the magnitude of the frictional force.

Figure 1.

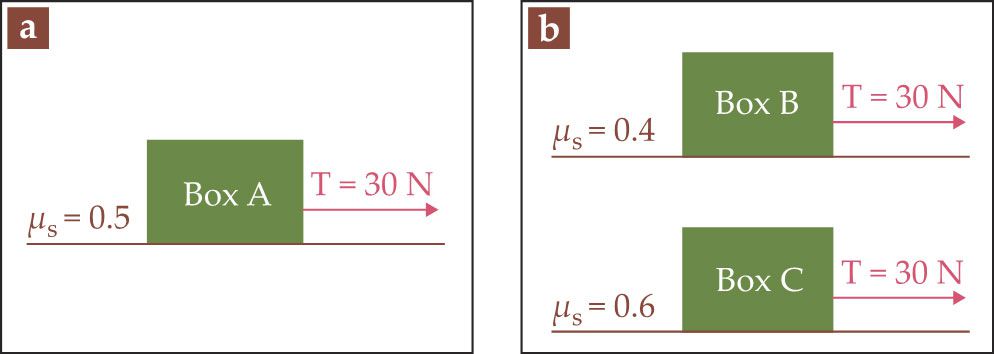
As an instructor, you might be tempted to celebrate that little instructional victory. But then you ask your students a follow-up question about two identical boxes on surfaces with differing roughnesses, as shown in figure 1b. Both boxes remain at rest when pulled by horizontal forces of equal magnitude. You notice that many students seem to abandon the correct reasoning they formerly applied. Instead, they argue based on their intuition that the rougher surface under box C means that it must be subject to a greater frictional force.

The inconsistency in reasoning highlighted in that vignette may be familiar. Students who demonstrate desired knowledge and reasoning on one question often abandon that approach on closely related problems—even when those follow-up questions are posed just minutes or seconds later. That tendency can persist even after extensive instruction devoted to conceptual understanding and qualitative reasoning. As an instructor, you may wonder why students apply concepts, principles, and intuition in such a selective manner. More importantly, if students do possess the knowledge necessary to reason productively, why don’t they catch their mistakes?

Reasoning inconsistencies can be puzzling and frustrating to both instructors and students. Yet research in cognitive psychology suggests that they are a result of general human processes of thinking and decision making—and are thus normal, expected, and inevitable. In fact, studies show that experts use those same thinking processes to their advantage. Thus instructors should be able to anticipate and address inconsistencies in student thinking in a manner that encourages further learning and reduces frustration.

Our research on the teaching and learning of physics demonstrates that dual-process theories (DPTs) of reasoning, popularized by psychologist Daniel Kahneman, provide a useful lens for understanding how both novices and experts reason in physics. ¹ DPTs model thinking in terms of both a fast, automatic process and a slow, effortful process. The theories allow us to pinpoint mechanisms contributing not only to incorrect answers and reasoning difficulties but also to productive expert-like reasoning pathways. In this article we describe how DPTs model human cognition and then apply them to the friction problem from the introductory vignette. We also present an analogy for DPTs that suggests some implications for physics instruction.

Dual-process theories

Since the early days of scientific inquiry into the human mind, researchers have worked toward developing general models of cognition that explain reasoning and decision making in all contexts. That work has led to DPTs, an influential family of models that are strongly supported by both neural imaging and laboratory studies that have examined participants’ performance on various cognitive tasks. ^{2 , 3}

Most DPTs share the same key features. They model human cognition in terms of interactions between two processes: a fast, automatic, and subconscious process and a slow, effortful, and deliberate process. Following other researchers, we will refer to the former as process 1, or the “intuitive” process, and the latter as process 2, or the “analytic” process.

The differences between the two can be illustrated by the following question: “A bat and a ball cost $1.10 in total. The bat costs $1.00 more than the ball. How much does the ball cost?” ⁴ For most people, the answer 10¢ springs to mind from process 1. In fact, many immediately and subconsciously embrace that answer as correct without giving it any further consideration. Once it is revealed that it is incorrect, however, most can determine through process 2 that the correct answer is 5¢. Thus process 1 provides an immediate response; process 2 is needed to examine the situation more carefully and determine the correct one.

The interplay between a quick, automatic response and more deliberate processing can also be observed in student performance on physics problems, as illustrated in the opening vignette and other examples from our studies. ^5–7 Specifically, when one is confronted with a new task, process 1 quickly makes associations between contextual cues and past experiences and produces a provisional mental model. In the case of our vignette, a student may associate more roughness with a greater frictional force and base their response on that model. The model cued by process 1 might be applicable in other contexts—that is why it is a learned association—but not necessarily to the situation at hand.

Incorporating intuition

DPT models also help researchers build a more formal characterization of intuition. Physicists value intuition and rely on it when practicing physics. Often, physics instructors stress that they want their students to develop physical intuition without carefully defining what that means. How can educators improve instruction toward a goal that is so vaguely defined? Although a precise definition of physical intuition remains elusive, DPTs offer some clues. Social scientist Herbert Simon once provided a parsimonious and pragmatic definition of intuition as “nothing more and nothing less than recognition.” ⁸ In other words, intuition is the outcome of process 1: It is a quick and unconscious model or impression arising from associations based on past experiences. When a person says, “my intuition is that …,” they mean, “process 1 is telling me …”

Although physicists claim to value intuition, sometimes it is viewed negatively. For example, when a student’s intuition leads to an erroneous response, their thinking is often described as everyday or informal and contrasted unfavorably with supposedly more sophisticated formal and analytical thinking. Yet intuition is also an indispensable component of expertise. ^{9 , 10} Experts possess an extensive repertoire of prior experiences, including recovery from errors, and learn to recognize appropriate cues and associate proper models. In fact, experts often automate formal processes so that they become effortless and intuitive. For instance, physicists may use intuition from their experience with conservation laws to constrain possible outcomes of a physical situation.

In the case of our introductory vignette, an expert will intuitively know that Newton’s second law is the relevant concept and rapidly recognize that the question is about balanced forces. Their experience will lead them to correctly ignore seemingly alluring yet extraneous information, such as the differing coefficients of static friction. For the expert, intuition thus provides a quick, effortless solution and conserves cognitive resources for more challenging situations.

Importantly, according to DPTs, the quick, subconscious process 1 cannot be turned off; we all perceive the world around us through its lens. It is overwhelmingly prevalent in everyday life, in which it is highly efficient and quite accurate in guiding judgments most of the time. As such, the output of process 1 serves as the entry point in most reasoning paths. The slow and deliberate process 2 may intervene to evaluate the output of process 1, but if a reasoner is confident in their first impression—for example, “the ball costs 10¢”—process 2 is circumvented and the first available mental model yields the final response. In physics, that can lead to reasoning pitfalls.

Reasoning pathways

To illustrate DPT models in greater detail, consider the opening vignette. In figure 2 we illustrate pathways to a solution to the problem, as predicted by DPTs of reasoning, along with four possible hazards, A–D.

Figure 2.

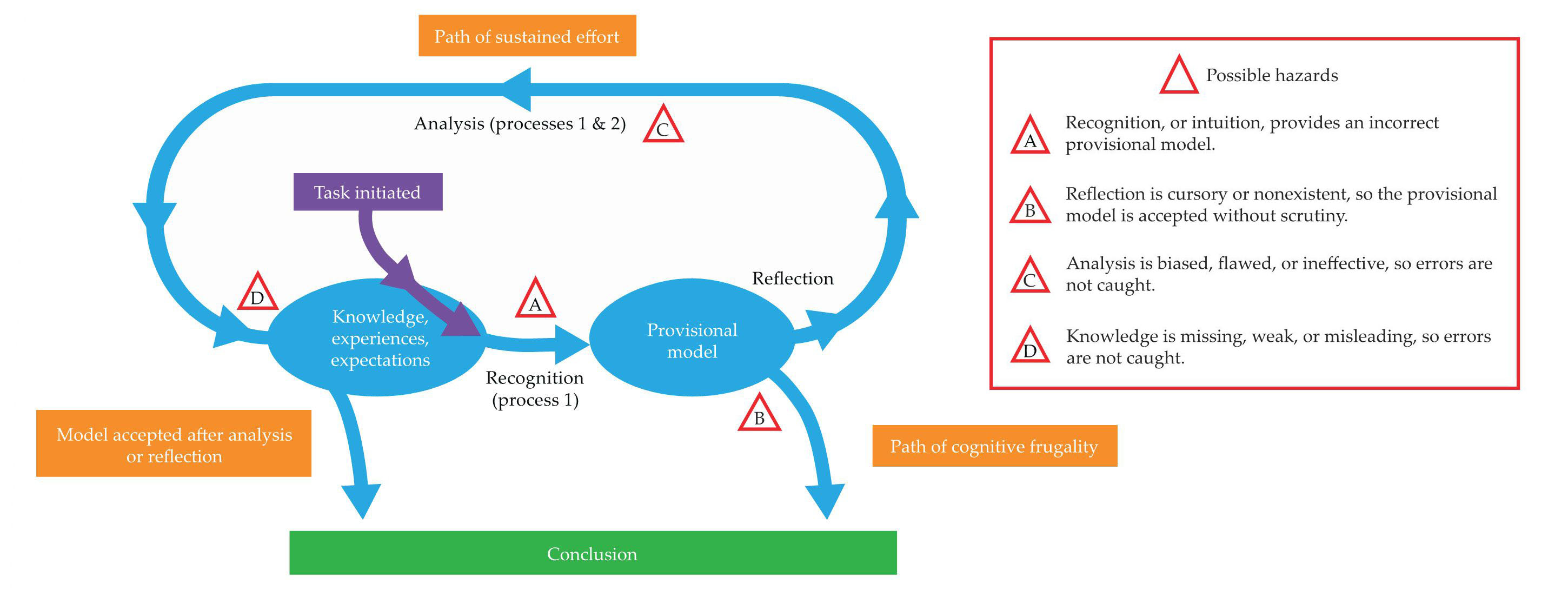
The first step is recognition, which is led by process 1. After reading the question, the student subconsciously recognizes a provisional mental model based on prior experiences, expectations, and contextual cues. In the case of the vignette, the problem contains two main features that compete for attention. The salience of an irrelevant feature—namely, the differing coefficients of static friction μ_s—will distract many students from the relevant feature, which is that the boxes remain at rest. As a result, process 1 prompts many students to erroneously interpret the problem as being about frictional forces and surface roughness.

That intuitively appealing but incorrect model, illustrated by hazard A in figure 2, presents the first potential setback on the path to a correct conclusion. Other students—and presumably experts—recognize that the situation concerns an object at rest and requires an application of Newton’s second law. That more accurate provisional model puts them on a path to a correct final response that avoids hazard A.

The second step involves a bifurcation: reflection versus final decision. After the initial mental model is formed, it can be scrutinized by the slow, logical, deliberate, and analytic process 2. However, if a reasoner feels confident in the accuracy of their first intuitive response, the analytic process may be circumvented, which results in a final decision based only on intuition. Such a direct path from the first intuitive mental model to a conclusion is said to stem from “cognitive miserliness,” a universal human tendency to spend the least amount of effort on a cognitive task. We believe that student responses that contain nothing but a statement such as “friction is greater because μ_s is greater” are likely a product of that reasoning shortcut.

Direct paths from an intuitive mental model to a final response can sometimes be desirable. An expert whose provisional mental model is consistent with a normative response does not need to engage the analytic process 2 to answer correctly. For that reason, we prefer the term “cognitive frugality” to cognitive miserliness. Frugality on some tasks is necessary if more computationally demanding tasks are to be tackled. Knowing when it is safe to proceed with the output of process 1 and when it is important to scrutinize that output is essential. Reasoners with more highly developed cognitive reflection skills will navigate that juncture more effectively and engage the analytic process when appropriate. ^{4 , 11} Failure at that point is represented by hazard B in figure 2.

Analyzing mental models

If the reasoner avoids hazard B, the third step is explicit analysis. Here, again, there are several ways such an analysis can fail. For example, reasoners tend to struggle with searching for alternative solutions or generating counterarguments. ¹² As such, the analytic process may be influenced by a process 1 form of confirmation bias in which cognitive resources are devoted to rationalization rather than error detection.

For example, a student who thinks that the coefficient of static friction μ_s is relevant to the problem posed in the opening vignette will find quick confirmation for that approach in a mathematical expression, F_fr = μ_sN, where F_fr is the frictional force and N is the normal force that the surface exerts on the box. That expression is not applicable to the vignette, but it is often cited by students to validate a response they already believe to be correct. Such biased or flawed reasoning presents another significant obstacle on the path to a valid conclusion, and it is depicted by hazard C in figure 2.

Another threat to the validity of the analytic process is a lack of a sufficiently robust conceptual framework to evaluate the output of process 1. For example, some students who are successful at applying physics knowledge in straightforward situations, such as an object at rest, may not know how to use that knowledge to evaluate an intuitively appealing response in a more complex situation that involves significant distractions. They may rely on criteria other than consistency with Newton’s laws to establish the validity of their argument. For instance, they might argue that “different coefficients of friction are given, so they must be relevant to the solution” or that “the formula F_fr = μ_sN has worked successfully in solving many other physics problems and therefore is likely to work here as well.”

In fact, some tend to dismiss the outcome of qualitative reasoning if it appears to disagree with a mathematical formula because they perceive formulas to be higher in the hierarchy of reasoning tactics in physics. One student, for example, admitted to us that “people would probably think that the friction is the same in both cases because neither box moves, but after applying the formula for static friction, you can see the force of friction is different.” In other words, an incorrect intuition-based mental model can often persist and lead students to an erroneous final response.

If correct and relevant formal knowledge is absent or is not developed to the degree needed to support detecting and overriding errors, students who engage the analytic process 2 will likely be unsuccessful. That is indicated by hazard D in figure 2. One student described their failed attempt as follows: “I tried to formally think it through by trying to remember the magnitude equations and by thinking of the different forces or anything that may be relevant to the problem. I was uncertain with my formal thinking attempt, so I went with my intuitive reasoning.”

Students who avoid hazard B—accepting the provisional mental model without scrutiny—are following a line of reasoning that we term the path of sustained effort, which is also shown in figure 2. That path can be iterative. If the first loop is completed without detecting red flags in reasoning, a response based on the provisional model is accepted and a conclusion is reached. However, if a reasoner identifies a need to consider alternatives, their process 1 may suggest a different provisional model cued by either the same or a different set of ideas, experiences, or expectations. In that case, the reasoning process persists and may undergo multiple iterations. As a result of that iterative reasoning process, the student may be able to successfully override the incorrect provisional model or models and reach a correct final response.

The more reasoning hazards a person must overcome during the analytic process, the more likely they will yield to the intuitive appeal of their initial model. The reasoning path that involves detecting and overriding errors is often cognitively expensive and emotionally unsettling. It is not surprising, then, that it is also frequently avoided. Adam, an introductory-physics student, provided a nearly perfect response to the question posed in the vignette: “[The] forces of friction are equal…. Since the boxes have equal force applied while remaining stationary, the friction will also be equal. The μ_s value is used more for maximum friction before being overcome.” Adam not only compared the frictional forces correctly but also articulated why the coefficients of static friction are irrelevant to the question. Yet even he admitted some uncertainty upon finishing the friction task: “I applied the formal reasoning to the best of my ability, unless I thought myself into a wrong answer, which would look idiotic.” ¹³

The terrain analogy

Human reasoning’s dual nature suggests that formal knowledge alone may not be sufficient for productive reasoning. Situations that tend to elicit intuitively appealing but incorrect responses are plentiful in physics. Because people cannot turn off the intuitive process 1, error detection mechanisms must be highly effective if they are to identify and override an initial mistake. Moreover, individuals must be motivated to tolerate the demands of the analytic process 2. We therefore argue that instructors should take the dual nature of reasoning into account and help students develop strategies for navigating reasoning challenges that can be likened to negotiating treacherous terrain.

The terrain analogy is useful for understanding instructional implications. Imagine that the task you set for your students lands them at an initial position in a hilly region (see figure 3). They don’t have a map, but they expect their destination to be the lowest point in the terrain. Although they may not recognize it, the journey to the actual destination requires them to traverse a hill—or, in the problem, to expend some cognitive effort. However, process 1 provides them with an initial direction along an easy path. Arriving at a local minimum (the position marked as the intuitive response in figure 3), students may not recognize that it is not the actual desired destination.

Figure 3.

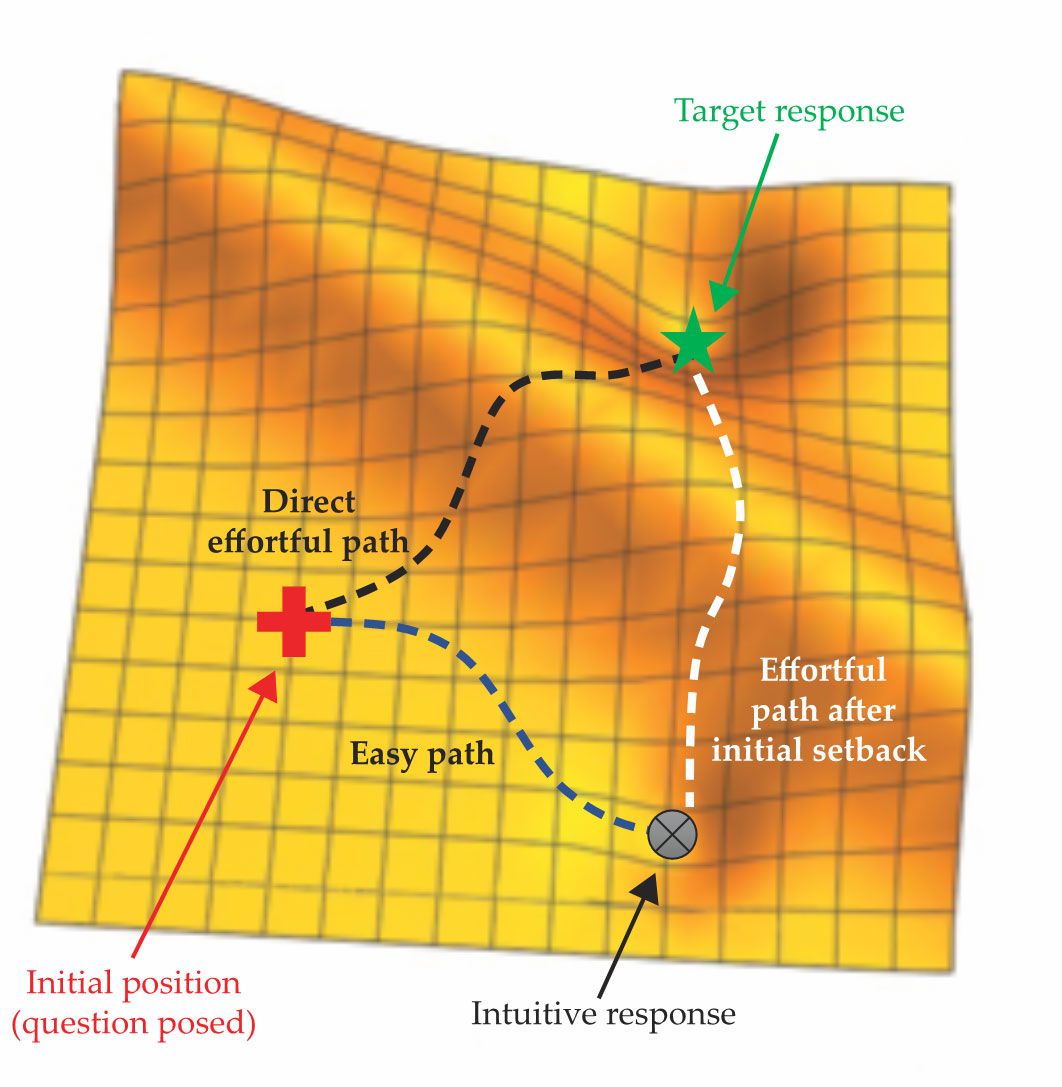
Our opening vignette can be applied to the terrain analogy. The destination (realizing that the frictional forces are the same) is located on the other side of a steep hill that requires effort to traverse (overriding the appeal of the intuitive response and applying Newton’s second law). The information about coefficients of static friction, however, suggests an easy stroll to an attractive depression in the terrain (larger μ_s means larger frictional force).

That location satisfies several criteria associated with the desired destination: an unambiguous answer supported both by prior experience with problems in which friction is linked to surface roughness and by mathematical authority in the form of a familiar equation. Because of those criteria, it is easily mistaken for the sought-after destination. Climbing out of the depression and exploring more terrain is rejected by many students as an unnecessary expenditure of effort (cognitive frugality).

Although some stay contentedly in that local minimum, expert reasoners quickly recognize that the easy path, although attractive, is not the way to their destination. Equipped with endurance, techniques, and superior travel gear—that is, motivation, reasoning skills, and formal knowledge—such experts are able to scale the ridge with confidence by using the direct effortful path to the target response, illustrated in figure 3. Even if experts are briefly led astray, their tendency to explore, using their cognitive reflection skills, may enable them to detect a navigation error, emerge from the alluring depression, and proceed to scale the ridge (indicated in figure 3 by the effortful path taken after the initial setback).

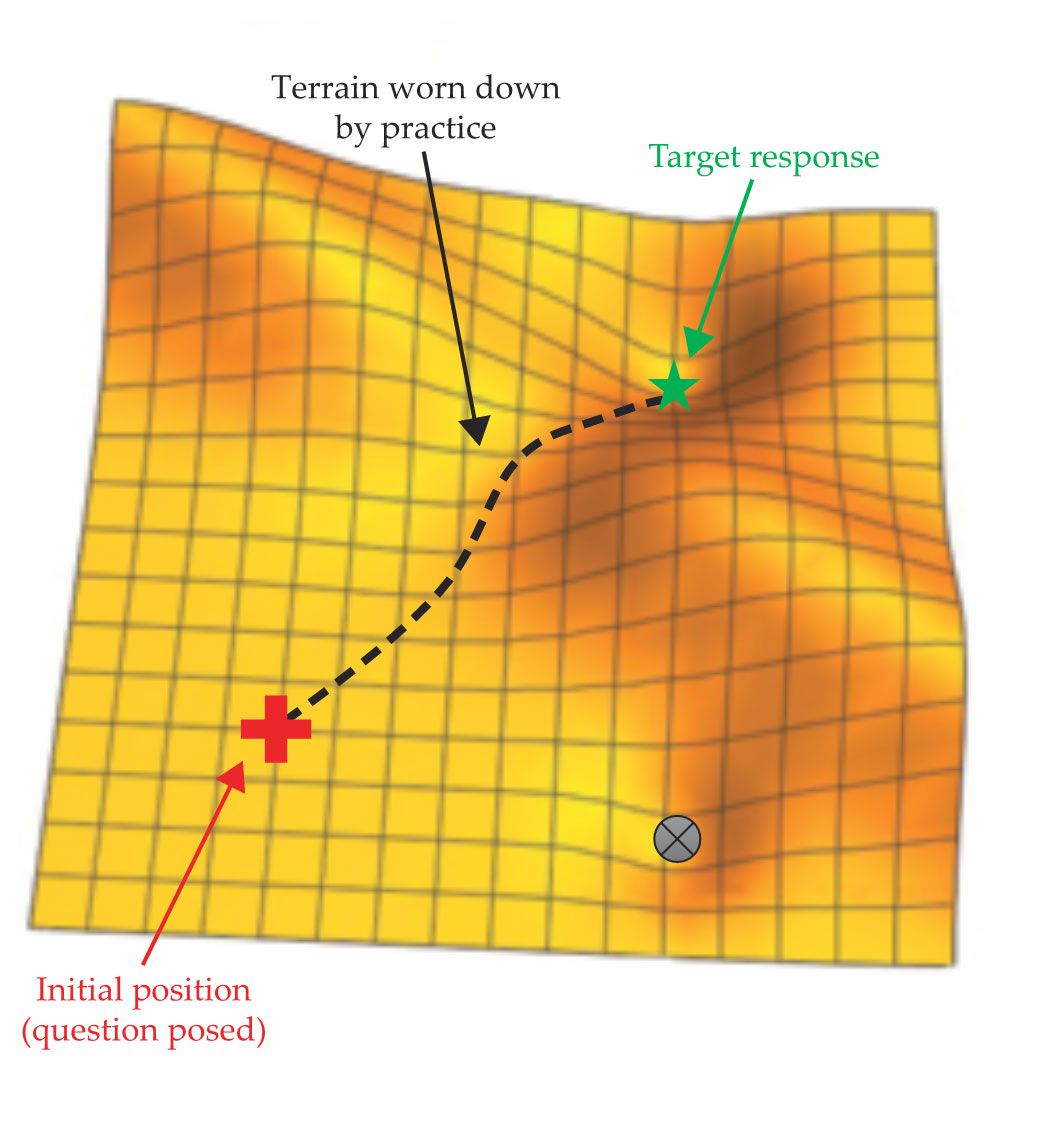
Experts also have another potential scenario. Their path to the target may be so well traveled that it has altered the topography of the terrain itself, as shown in figure 4. Because those experts have worn down the path by years of extensive practice, they no longer require much effort to traverse it. For them, the automatic and effortless path suggested by process 1 and the desired path are now one and the same.

Figure 4.

Instructional implications

The terrain analogy suggests two strategies for helping students. Both have benefits and drawbacks.

The first approach is to primarily focus on flattening the terrain and automating the direct path to the solution—that is, altering the likely outcome of process 1. If students repeatedly practice short sample problems, they will begin to recognize the path to the correct destination on similar problems. Such an approach will eventually wear down a direct path through the mountain range and allow students to determine the solution with little cognitive load. That means that process 1 is now likely to lead to a rapid, low effort and accurate outcome without engaging process 2.

One significant disadvantage to that approach is that it is unlikely to help students develop the skills necessary to navigate unfamiliar terrain and solve other kinds of problems. If they only receive instruction aimed at flattening the terrain, minor deviations from a well-traversed path or relatively small changes in the destination may leave students feeling lost, frustrated, and unprepared.

The second approach is to improve students’ endurance, technique, and “hiking gear”—that is, to boost the likelihood that process 2 will be engaged successfully. It focuses on using deliberate reasoning, planning solution paths, analyzing alternatives, and evaluating results. To teach those higher-level skills, instructors should give students varied and challenging problems and help them thoughtfully and deliberately practice general reasoning and problem-solving strategies.

Part of that approach is aimed at helping students develop robust strategies for recognizing when they are on the right path or have reached the right destination—that is, detecting errors and overriding them. Research shows that quick fixes, such as using a single example to address novices’ common intuitive responses, are unlikely to lead to a long-lasting effect. ⁵ But that does not mean that cognitive reflection cannot be taught. One effective way to help students develop general reasoning strategies is to elicit their intuitive process 1 responses to various problems and then provide guidance on how they can evaluate those responses.

Such an approach can help students recognize that some types of formal knowledge, such as Newton’s second law, can be used both as a tool for solving a problem (for example, for an object at rest, forces must balance) and as a criterion for checking the validity and physical consistency of a provisional response (for example, if the static frictional force increases because μ_s increases, is Newton’s second law still satisfied?). ⁶ In particular, we argue that instructors should help students cultivate the habit of questioning their intuitions. For example, students should be asking themselves such questions as the following: Is my model valid? What criteria must it satisfy to be valid? Is it consistent with other relevant physics principles? Returning to the terrain analogy, that approach should help students wander, get lost in a ravine, reflect, find a way out, and navigate through difficult terrain to the solution.

Training processes 1 and 2

There are trade-offs to the approaches described above. Although automating the solution path can optimize speed and reduce cognitive load, one cannot practically train on all possible problem paths. On the other hand, each task that arises should not require careful and effortful analytical thinking. Indeed, one hallmark of an expert is how they automate a significant number of tasks. Think, for example, about how effortlessly a physics instructor builds an integral.

We argue that some processes need to be automated for introductory physics, such as crucial math skills like trigonometric, algebraic, and vector operations. Improving students’ fluency with essential skills enables their cognitive frugality on the basic steps needed for more complex reasoning. That, in turn, frees up their cognitive resources so they can engage in more computationally expensive analytic processes, such as reflection, the search for alternatives, and error detection. Those are particularly relevant for tasks for which an increased mastery of basic skills alone does not help students flatten the terrain sufficiently.

Overall, we propose that instruction should include both approaches. Focusing on process 1 is probably best for short, one- or two-step skills and knowledge. To improve such skills, teachers should use carefully designed, repeated, and spaced practice problems and give immediate feedback to build and retain fluency and reduce cognitive load. ¹⁴ In that way, students build one aspect of intuition by automating those skills. Initial studies on that type of approach are promising, although it remains an open question which skills lend themselves well to automation.

To help students develop approaches to productively engage process 2, instructors may need to provide repeated opportunities in multiple contexts. Such instruction will likely require making the interaction between the two processes visible to students. Instructors could present them with various scenarios, as seen in figure 2, in which hazard A is likely to be encountered. Those scenarios are likely to elicit misleading process 1 responses. Careful guidance could then be provided for navigating hazards B–D. As a result, students might learn how to reflect on an intuitively appealing response, use formal physics knowledge to check its validity, consider alternatives if a mistake is detected, and override a mistaken response.

Finally, and perhaps most importantly, we speculate that a style of physics instruction that makes the dual nature of thinking explicit and visible to students may affect teaching in ways that extend beyond improvements in student performance. It may help establish an instructional environment that emphasizes that careful examination and possible rejection of an intuitive response is a natural part of reasoning and not an indication of a lack of knowledge or any other deficiency on the part of the student.

Rather than learn to reflexively discount their intuitions, students should be taught that intuition and formal knowledge are both important and can—and often do—interact fruitfully. Such a reframing may also help address a common concern that incorrect intuitive responses may lead to feelings of inadequacy, such as a student saying, “I am always wrong when it comes to physics, so I am not good enough to stay in the major.” Classroom discussions emphasizing that initial incorrect responses often stem from the dual nature of human thinking may help alleviate such concerns and help bolster students’ sense of self-worth and belonging in physics.