Earth’s enigmatic inner core
DOI: 10.1063/PT.3.2178
If we could travel to the center of Earth, we would leave behind the rocky outer shell and enter the liquid iron core about halfway down. After we traversed 80% of the distance to the center, the liquid iron core would transform into a solid due to the crushing influence of pressure, even though the temperature is comparable to the surface temperature of the Sun. Crossing into the solid region brings us to Earth’s inner core. Figure 1 illustrates the principal subshells that make up the planet.
Figure 1. A cross section of Earth’s interior reveals a rocky outer shell (mantle) and a metallic core. The core is made up mostly of iron, although impurities lower the density below that of pure iron. The gradual solidification of the liquid outer core produces a solid inner core. The density of the inner core is more consistent with pure iron, which implies a lower concentration of impurities than are in the surrounding liquid. (Figure courtesy of Eric King.)
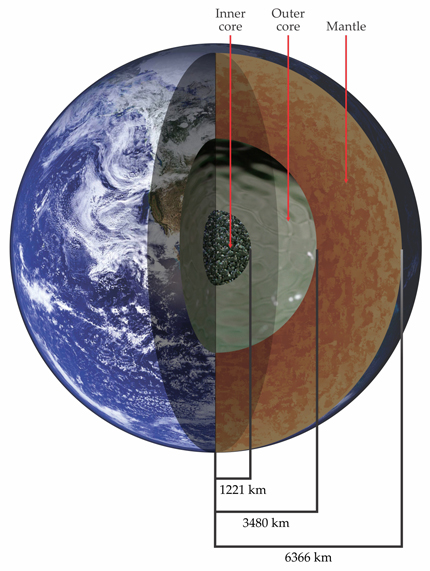
Despite its small size–less than 1% of Earth’s volume, with a radius the width of Texas–the inner core has a surprisingly large role in the dynamics of our planet’s interior. Earth’s gradual cooling causes the inner core to grow at roughly 1 mm/yr by solidification of the liquid surrounding it. The release of latent heat and the exclusion of impurities in the liquid iron produce buoyant fluid that stirs the outer core and generates Earth’s magnetic field. Indeed, more than half of the power currently needed to generate the magnetic field is probably derived from inner-core growth. 1
Propagating seismic waves through Earth illuminates the planet’s internal structure much as x rays illuminate features of the body in medical imaging: Differences in physical properties alter the waves’ absorption, scattering, and transmission, which permits the structure to be reconstructed from surface observations. A growing collection of observations reveals unexpected complexity in the inner core. Evidence for lateral variations in seismic-wave speed and attenuation is inconsistent with simple expectations of slow radial growth from a well-mixed liquid. More enigmatic is the evidence for elastic anisotropy, which causes seismic waves to travel several percent faster along polar paths than equatorial paths.
There is no consensus on the origin of elastic anisotropy or most of the other structure, but researchers suspect that the complexity is a record of past dynamics. Understanding how to read that record offers an opportunity to gain new insights into the history of our planet; it may also reveal the reasons why Earth evolved so differently from its nearest planetary neighbors.
Discovery and surprises
In 1936 seismologist Inge Lehmann proposed the existence of an inner core, based on the reflection of seismic waves from its surface. 2 Proof that the inner core is actually solid would have to wait 35 years until measurements of Earth’s elastic normal modes confirmed the need for finite rigidity at the planet’s center. 3 That observation supported the prevailing view that the inner core forms by solidification and grows outward as Earth cools. Thermal modeling suggests that the inner core’s diameter has grown by 8 cm since the time of its discovery—far too small a change to detect in seismic-wave observations.
Most modern studies rely on differential travel-time measurements, which compare the propagation times of waves that pass through and just above the inner core. Careful selection of earthquake and receiver locations establishes propagation paths that are nearly coincident through much of Earth’s interior, so anomalies in the differential travel time can be attributed mostly to propagation through the inner core, as outlined in figure 2. In the mid 1980s evidence for the elastic anisotropy in the inner core began to appear; 4 independent support for it also came from observations of seismic normal modes, which represent elastic vibrations of the entire planet.
Figure 2. Seismic waves illuminate Earth’s internal structure. Compressional waves that travel from one location (designated by the star)—typically an earthquake—through the mantle (green) and core to another location on the surface are often denoted PKP. Different paths through the core are possible. (a) The sets of paths AB (red) and BC (blue), which differ in the extent of refraction they experience at the core–mantle boundary, travel entirely through the liquid core (pale yellow). (b) Paths DF (purple), in contrast, travel through the inner core (orange) as well. Differences in the travel time between the BC and DF paths are primarily due to propagation through the inner core and thus can be used to discern aspects of its structure. (Figure courtesy of Ed Garnero.)
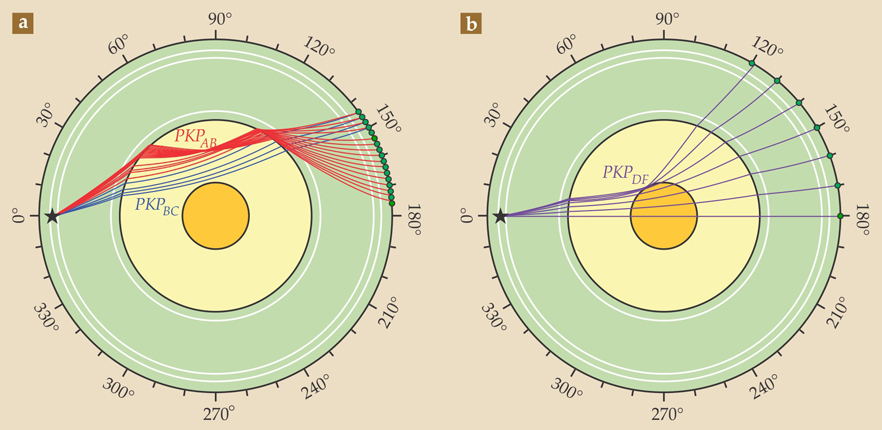
The unexpected discovery of elastic anisotropy initiated a flurry of activity. As subsequent studies provided more thorough coverage of the inner core, the complexity required to explain the observations steadily increased. Several consistent features emerged, including hemispherical differences in the strength of anisotropy: 5 Strong anisotropy is required in the western hemisphere to account for large travel-time anomalies, whereas weak anisotropy is sufficient to explain the behavior of waves that pass through the eastern hemisphere. There is little evidence for anisotropy in the top 100 km of the inner core, but support is growing for a distinctly oriented anisotropy at the inner core’s very center. Limited observations suggest that the slow direction is tilted by 45° from the equatorial plane. 6
Another surprise was the discovery in the mid 1990s of anisotropy in the attenuation of seismic waves. 7 Higher attenuation of the waves’ intensity in the inner core is often associated with faster propagation speeds. That behavior is opposite to the usual dispersive effects in imperfect elastic solids. Scattering of seismic waves is a likely explanation, possibly due to regions of distinctly oriented iron crystals in the inner core. Explaining the large-scale anisotropy in attenuation requires scatterers that are both aspherical and preferentially aligned.
Interestingly, a strong correlation between wave speed and attenuation is also found in regions, such as the upper 100 km, that lack strong elastic anisotropy. For example, wave speeds in the upper 100 km appear to be nearly isotropic, yet geographic areas with high attenuation tend to correspond to higher-than-average wave speeds. One suggestion is that variations in the size of iron crystals in the top 100 km of the inner core could account for both the attenuation and velocity. 8 Crystal sizes ranging from tens of meters to tens of kilometers may be enough to explain the observations, but those crystals would need to be randomly oriented in the upper 100 km of the inner core to ensure that the velocity in that particular region remains nearly isotropic.
Thermal models
Growth of the inner core cannot be detected in observations, but it can be predicted using models for the thermal evolution of the core. Cooling is driven by heat conduction into the base of the rocky shell that surrounds the core. That shell, known as the mantle, is more massive than the core and has a high effective viscosity, which accommodates slow thermal convection with velocities on the order of 0.1 m/yr. Comparatively rapid flows on the order of 104 m/yr can be driven in the low-viscosity liquid core by temperature anomalies of only a few millikelvin. 9 Ultimately, convection in the mantle regulates the cooling of the core and sets the pace of inner-core growth.
Temperatures in the core were probably high enough in the distant past to ensure that the entire core was liquid. Gradual cooling eventually caused the temperature at Earth’s center to drop low enough to nucleate an inner core. Solidification begins at the center because of the pressure dependence of iron’s melting curve, shown in the
The rate of inner-core growth is set by the average heat flux into the base of the mantle. Cooling drives solidification, but the release of latent heat reduces the resulting change in temperature. In addition, impurities in the liquid-iron core are excluded from the solidifying inner core, judging from seismic estimates of the density change across the inner-core boundary. Those impurities produce buoyant fluid that helps to stir the liquid core. The result is a segregation of impurities into the liquid core and a decrease in Earth’s gravitational potential energy. Nearly all of that energy ends up in the core as heat, which also buffers the change in temperature. The inner core’s evolving composition can further slow the rate of solidification for a prescribed heat flux.
Models for inner-core growth are hampered by substantial uncertainties in many of the relevant physical properties, but most recent models suggest that the inner core grew to its current size in 1 billion years or less. 1 Before that time, convection in the core would have been driven primarily by cold, dense fluid sinking from the core–mantle boundary as the core cooled. Peter Olson describes the dynamics of convection and magnetic field generation in the companion article on page 30 .
Dynamics
Geological observations of magnetization in ancient rocks demonstrate that Earth has possessed a magnetic field for at least the past 3.2 billion years. 10 The persistence of the magnetic field implies that the liquid core has been convectively stirred for most of Earth’s history. Once an inner core formed, its growth introduced new physical processes; a record of those processes is imprinted on the growing sphere.
Thanks to the low viscosity of liquid iron, the solid inner core can rotate relative to the mantle. Early numerical models of convection and field generation 9 in the liquid core predicted inner-core rotation rates of roughly one degree per year. In those models, eastward flow at the base of the liquid core carried the inner core in the same direction on average.
A subsequent search for the rotation by seismologists revealed an intriguing change in travel time for waves that propagate through the inner core. 11 Waves that travel from nearby earthquake locations to fixed receivers on the surface pass through different parts of the inner core if it rotates with time. Initial estimates for the change in travel time were interpreted as eastward rotation of the inner core, although several subsequent studies have challenged the existence of any rotation; 7 inner-core rotation is plausible on physical grounds, but its detection in seismic observations remains controversial.
Another type of motion is caused by the thermal convection inside the inner core. In the absence of substantial heat sources, convection is expected when rapid growth of the inner core leaves little time for conductive cooling. In that case, warm, buoyant material develops below colder, dense material. Such a density stratification is unstable to convective overturn by creeping flow, even though the inner core is solid. By contrast, slow growth of the inner core allows time for conductive cooling, which in turn allows material at the center of the inner core to become cold and dense. And in that scenario, the density stratification is stable and convection will not occur. Current estimates suggest that the inner core lies close to the transition between stable and unstable stratification. Changing the value of thermal conductivity within the present uncertainties is enough to switch between convecting and nonconvecting states.
Even if the inner core was convectively unstable at early times, a number of factors can subsequently suppress convection. Latent heat release and chemical segregation become more important in the heat budget of the core as the inner core grows in size. As a result, the rate of growth inevitably decreases with time and may eventually tilt the balance in favor of a stable thermal stratification. In addition, an increasing concentration of impurities in the liquid core can drive slightly higher levels of impurities into the solid during subsequent growth. A stable, chemical stratification can develop with time, particularly when the inner core becomes large, although the details depend on how impurities partition between the liquid and solid phases at high pressures and temperatures. There is plenty of uncertainty—even the identity of the impurities is not firmly established.
A surprising form of thermal convection is permitted by the presence of a phase transition at the inner-core boundary. 12 The usual form of convection—with a closed circulation of rising and sinking motion—is replaced by a nearly rigid-body translation. Melting in one hemisphere and solidification in the other closes the convective circulation. Two conditions are required for translational convection to occur. First, the inner core must be convectively unstable; second, its viscosity must be high enough to ensure that its shape changes primarily by melting and solidification rather than by viscous flow.
Rigid-body translation is strongly coupled to convection in the liquid core because melting and solidification depend on heat and the transport of material above the surface of the inner core. Simple parameterizations of turbulent transport have been used so far to describe the response of the liquid core, 12 but complications can arise from a combination of geometry, rapid planetary rotation, and the presence of a magnetic field. Surprises are waiting to be discovered as better models for coupled convection are developed.
The preceding discussion should dispel any notion that the inner core is static; instead, it is swept around by convection in the liquid core and may undergo its own internal convection. Even if the inner core is not convectively unstable, it is still subject to many other forms of deformation. For example, electric currents can produce heterogeneous heating. 13 That heating is not sufficient to drive convective overturn, but it can produce lateral variations in temperature, which induce a creeping flow.
In addition, the inner core is expected to solidify preferentially in the equatorial region due to the nature of heat transport in the overlying liquid. If the viscous flow of material is the primary means of relaxing boundary topography, then a large-scale flow can develop in the interior. 14 Flow may also be driven by magnetic stresses on the inner core, 15 possibly connected with inner-core rotation. Given the multitude of physical processes that can cause deformation, it is reasonable to ask if any of those processes can also explain the observed seismic structure of the inner core.
Origin of inner-core structure
Elastic anisotropy in the inner core, illustrated in figure 3, is one of the earliest and most enduring mysteries to emerge from seismic observations. The presence of elastic anisotropy is usually attributed to preferential alignment of crystal lattices, although other structural features, such as oriented pockets of melt and large-scale chemical layering, can also give rise to anisotropy. A preferential crystal alignment, often referred to as texture, can be established at the time of solidification or may develop as a result of subsequent deformation.
Figure 3. Elastic anisotropy in the inner core causes compressional seismic waves to travel fastest in the polar direction. The magnitude of the anisotropy, designated by the length of brown rods in that direction, varies across the inner core. Anisotropy is strongest in the western hemisphere (longitude 270°) and is much weaker in the eastern hemisphere (longitude 90°); the green dashed line represents the equator. The innermost region (red) of the inner core is also anisotropic, but with an orientation (not shown) thought to be tilted with respect to the poles. (Figure courtesy of Xiaodong Song.)
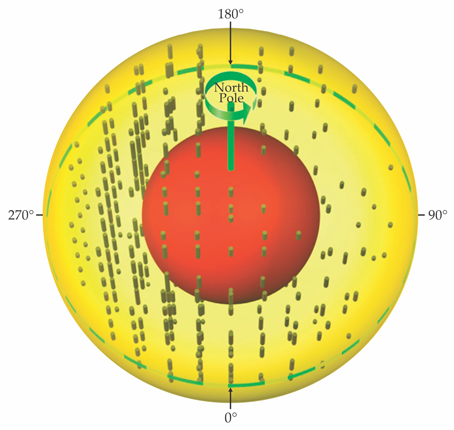
Laboratory experiments suggest that the orientation of temperature gradients during solidification can establish an initial texture. 16 Numerical models of convection and magnetic-field generation have shown that temperature gradients at the inner-core boundary are primarily radial, although the magnitude of such gradients can vary with latitude. Expectations for crystals to align in the radial direction are consistent with the absence of strong anisotropy in the top 100 km of the inner core because a radial structure is invariant under rotation and should not produce faster wave speeds in polar directions.
Subsequent deformation of material with an initial solidification texture can produce the observed anisotropy, but that deformation must be influenced in some way by rotation because it is unlikely for fast paths to align with the direction of the rotation axis by chance. The required deformation could arise in a variety of ways. For example, thermal convection in the inner core can align with the rotation axis, but only when the vigor of convection is relatively weak. Alternatively, preferential growth of the inner core at the equator can produce flow with a polar orientation as long as the viscosity of the inner core is not too high. It is also possible for electric currents and magnetic stresses to possess the correct symmetry because those features are associated with processes in the liquid core, which are strongly affected by the influence of rotation.
A second and more serious challenge is to explain the presence of hemispherical variations in elastic anisotropy. Electric currents, magnetic stresses, and local heat flow should all be heterogeneous over the surface of the inner core, but it is less obvious why the heterogeneity would be spatially persistent for long enough to establish a prominent deformation texture. A representative large-scale flow of several centimeters per year would produce strain rates on the order of 10−15 s−1 and would require about 107 years to accumulate enough strain to have observable consequences. If the inner core is free to rotate, one might expect significant averaging of structure in longitude, which would tend to erase hemispherical differences. Alternatively, the inner core may be locked in place by gravitational forces associated with mass anomalies in the mantle, although viscous deformation (or melting and solidification) can permit the inner core to escape the grasp of gravity. 17
Translational convection is often suggested as a possible explanation for hemispherical differences, 12 particularly the hemispherical variations in isotropic velocity in the upper 100 km of the inner core. 7 However, extending the idea to explain the variations in anisotropy presents several unsolved challenges. First, translation causes little deformation, so any initial solidification texture at the surface of the inner core would simply be carried along by the nearly rigid-body motion. It is not clear how a strong anisotropy would develop in one hemisphere and disappear in the other without any additional deformation. Second, translation cannot explain the distinctly oriented anisotropy in the central part of the inner core (red region in figure 3). There is currently no simple explanation that accounts for all of the complexity of the seismic observations.
Gaining perspective
The seismic observations are, in a word, confounding. Simple expectations for slow growth of the inner core from a well-mixed liquid are completely at odds with clear evidence for structural complexity. Proposals abound to explain one aspect or another, but none currently provide comprehensive understanding. The attention given to the inner core may be surprising to some, given its small size, but there are few records of past dynamics in Earth’s core. Fluctuations and reversals in Earth’s magnetic field are recorded in rocks at the surface (see the article by David Dunlop, Physics Today, June 2012, page 31 ), but the inference of internal dynamics is indirect because the magnetic dipole at the surface represents only a small fraction of the field inside the core. If the inner core is a battered relict of 1 billion years of evolution, then much can be learned from its seismic structure. In many ways the inner core is analogous to a rock outcrop for a geologist. Long and elaborate tales have been told from a small patch of rock, and the same may be true for the solid iron ball at Earth’s center.
Box. An outsized role for the inner core
Vigorous convection in Earth’s liquid core continually regenerates the planet’s magnetic field. An important source of buoyancy to drive the fluid motion comes from the growth of the inner core. Convective mixing homogenizes both the composition and entropy of the fluid, so the core temperature, plotted here (blue) as a function of radius, is well approximated by the condition of constant entropy. By comparison, the melting temperature of iron (red) is expected to have a stronger dependence on pressure. The intersection of the core-temperature and melting-temperature curves defines the radius of the inner core, which is currently 1221 km–about 20% of Earth’s radius. At that depth, the melting temperature is estimated to be about 5500 K. As the core cools, the intersection point shifts toward larger radius and the inner core grows by solidification.
References
1. F. Nimmo, in Treatise on Geophysics, vol. 8, P. Olson, ed., Elsevier, Boston (2007), p. 31.
2. I. Lehmann, Publ. Bur. Cent. Seismol. Int. A 14, 87 (1936).
3. A. M. Dziewonski, F. Gilbert, Nature 234, 465 (1971). https://doi.org/10.1038/234465a0
4. A. Morelli, A. M. Dziewonski, J. H. Woodhouse, Geophys. Res. Lett. 13, 1545 (1986). https://doi.org/10.1029/GL013i013p01545
5. X. Sun, X. Song, Earth Planet. Sci. Lett. 269, 56 (2008). https://doi.org/10.1016/j.epsl.2008.01.049
6. M. Ishii, A. M. Dziewonski, Proc. Natl. Acad. Sci. USA 99, 14026 (2002). https://doi.org/10.1073/pnas.172508499
7. A. Souriau, in Treatise on Geophysics, vol. 1, A. M. Dziewonski, B. A. Romanowicz, eds.,Elsevier, Boston (2007), p. 655;
A. Souriau, B. Romanowicz, Geophys. Res. Lett. 23, 1 (1996 1996). https://doi.org/10.1029/95GL035838. M. Monnereau et al., Science 328, 1014 (2010). https://doi.org/10.1126/science.1186212
9. P. H. Roberts, E. M. King, Rep. Prog. Phys. (in press).
10. J. A. Tarduno et al., Nature 446, 657 (2007). https://doi.org/10.1038/nature05667
11. X. Song, P. G. Richards, Nature 382, 221 (1996). https://doi.org/10.1038/382221a0
12. T. Alboussière, J. R. Deguen, M. Melzani, Nature 466, 744 (2010). https://doi.org/10.1038/nature09257
13. S.-I. Takehiro, Phys. Earth Planet. Inter. 184, 134 (2011). https://doi.org/10.1016/j.pepi.2010.11.002
14. S. Yoshida, I. Sumita, M. Kumazawa, J. Geophys. Res. [Solid Earth] 101, 28085 (1996). https://doi.org/10.1029/96JB02700
15. S. Karato, Nature 402, 871 (1999); https://doi.org/10.1038/47235
B. Buffett, H. R. Wenk, Nature 413, 60 (2001). https://doi.org/10.1038/3509254316. M. I. Bergman, Nature 389, 60 (1997). https://doi.org/10.1038/37962
17. B. Buffett, Nature 388, 571 (1997). https://doi.org/10.1038/41534
More about the Authors
Bruce Buffett is a professor in the department of Earth and planetary science at the University of California, Berkeley.
